Notice
Thomas Backdahl - Symmetry operators, conserved currents and energy momentum tensors
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
Conserved quantities, for example energy and momentum, play a fundamental role in the analysis of dynamics of particles and fields. For field equations, one manifestation of conserved quantities in a broad sense is the existence of symmetry operators, i.e. linear differential operators which take solutions to solutions. A well known example of a symmetry operator for the scalar wave equation is provided by the Lie derivative along a Killing vector field. It is important to note that other kinds of objects can generate symmetry operators. For waves in the Kerr spacetime there is a symmetry operator associated with Carter's constant. This symmetry, which is "hidden" in the sense that it arises from a Killing spinor, satisfying a generalization of the Killing vector equation, rather than a Killing vector, was an essential ingredient in a proof of decay of scalar waves on the Kerr background by Andersson and Blue. In this talk we will consider what conditions on a spacetime are necessary for existence of symmetry operators for the conformal wave equation, the Dirac Weyl equation, and the Maxwell equation, i.e. for massless test fields of spins 0, 1/2 and 1. We will investigate how the conditions for the symmetry operators for the different field equations are related, and how they are related to existence of conserved currents. Furthermore, these tools lead to the construction of a new energy momentum tensor for a Maxwell field on a Kerr background. This will provide a powerful tool for the study of decay of Maxwell fields on the Kerr spacetime.
Intervention / Responsable scientifique
Documentation
Liens
Dans la même collection
-
Maciej Zworski - From redshift effect to classical dynamics : microlocal proof of Smale's conjecture
ZworskiMaciejDynamical zeta functions of Selberg, Smale and Ruelle are analogous to the Riemann zeta function with the product over primes replaced by
-
Pieter Blue - Decay for fields outside black holes
BluePieterI will discuss energy and Morawetz (or integrated local decay) estimates for fields outside black holes. These results build on results for
-
Jérémie Szeftel The resolution of the bounded L2 curvature conjecture in General Relativity (Part 1)
SzeftelJérémieIn order to control locally a space time which satisfies the Einstein equations, what are the minimal assumptions one should make on its
-
Philippe G LeFloch - Weakly regular spacetimes with T2 symmetry
LeFlochPhilippe G.I will discuss the initial value problem for the Einstein equations and present results concerning the existence and asymptotic behavior of
-
Andras Vasy - Microlocal analysis and wave propagation (Part 4)
In these lectures I will explain the basics of microlocal analysis, emphasizing non elliptic problems, such as wave propagation, both on manifolds without boundary, and on manifolds with boundary. In
-
Claudio Dappiaggi - On the role of asymptotic structures in the construction of quantum states for …
DappiaggiClaudioIn the algebraic approach to quantum field theory on curved backgrounds, there exists a special class of quantum states for free fields,
-
Andras Vasy - Microlocal analysis and wave propagation (Part 1)
VasyAndrásIn these lectures I will explain the basics of microlocal analysis, emphasizing non elliptic problems, such as wave propagation, both on
-
Jérémie Joudioux - Hertz potentials and the decay of higher spin fields
JoudiouxJérémieThe study of the asymptotic behavior of higher spin fields has proven to be a key point in understanding the stability properties of
-
Alain Bachelot - Waves in the Anti-de Sitter space-time Ads
BachelotAlainIn this talk we address some issues concerning the wave propagation in the 4D+1 anti de Sitter space time : the role of the conformal
-
Lionel Mason - Perturbative formulae for scattering of gravitational wave
MasonLionel J.The Christodoulou Klainerman proof of existence of asymptotically simple space-times shows that it is reasonable to consider the scattering of
-
Andras Vasy - Microlocal analysis and wave propagation (Part 3)
In these lectures I will explain the basics of microlocal analysis, emphasizing non elliptic problems, such as wave propagation, both on manifolds without boundary, and on manifolds with boundary. In
-
Alexander Strohmaier - Workshop
StrohmaierAlexanderI will explain how one can formulate and formalize the Gupta Bleuler framework for the Quantization of the electromagnetic field in an
Sur le même thème
-
Tuan Ta Pesao : écritures de sable et de ficelle à l'Ile d'Ambrym
VandendriesscheEricCe film se déroule au Nord de l’île d’Ambrym, dans l’archipel de Vanuatu, en Mélanésie...
-
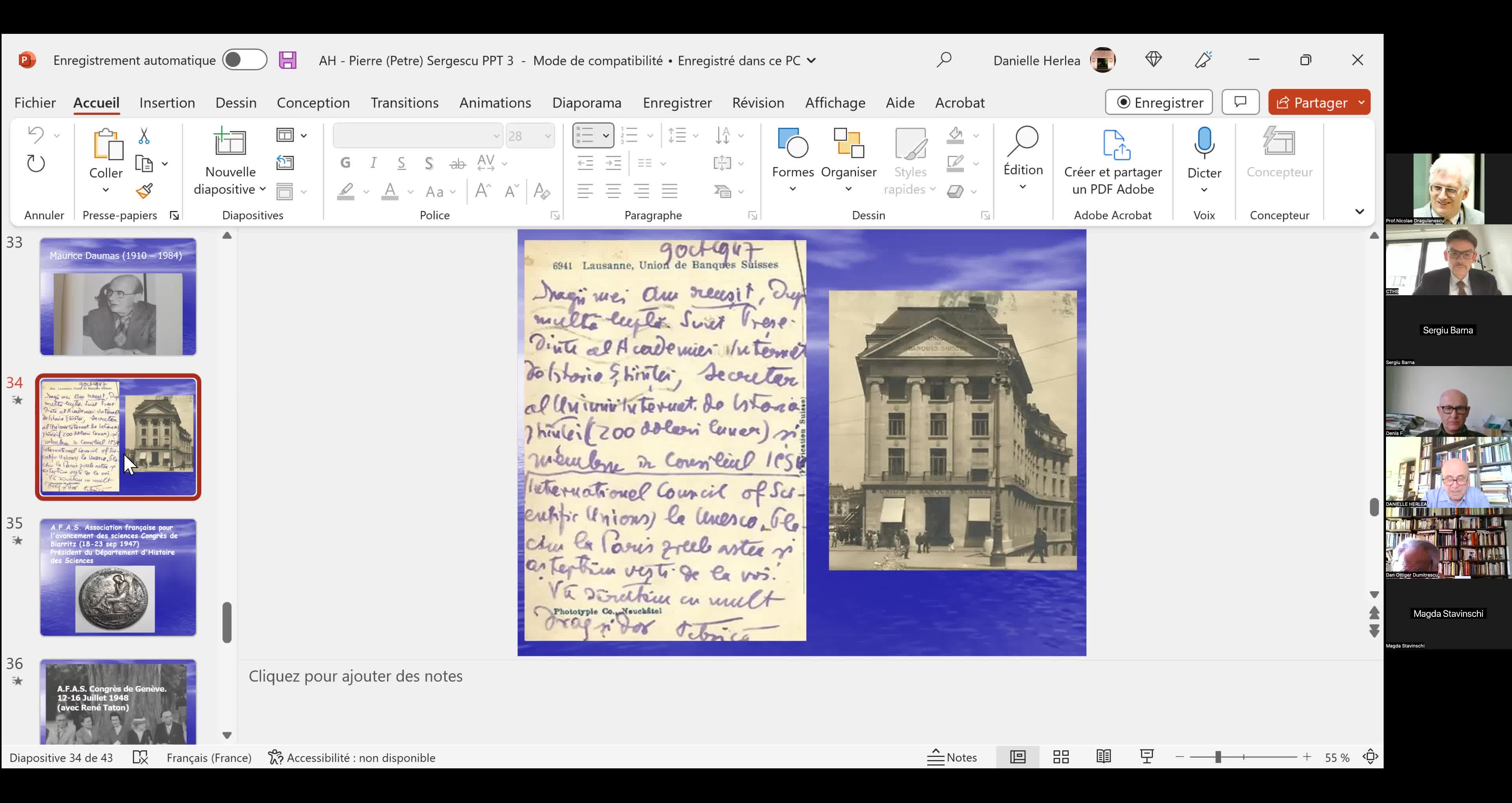
"Le mathématicien Petre (Pierre) Sergescu, historien des sciences, personnalité du XXe siècle"
HerléaAlexandreAlexandre HERLEA est membre de la section « Sciences, histoire des sciences et des techniques et archéologie industrielle » du CTHS. Professeur émérite des universités, membre effectif de l'Académie
-
Webinaire sur la rédaction des PGD
LouvetViolaineRédaction des Plans de Gestion de Données (PGD) sous l’angle des besoins de la communauté mathématique.
-
Alexandre Booms : « Usage de matériel pédagogique adapté en géométrie : une transposition à interro…
« Usage de matériel pédagogique adapté en géométrie : une transposition à interroger ». Alexandre Booms, doctorant (Université de Reims Champagne-Ardenne - Cérep UR 4692)
-
D. Stern - Harmonic map methods in spectral geometry
SternDanielOver the last fifty years, the problem of finding sharp upper bounds for area-normalized Laplacian eigenvalues on closed surfaces has attracted the attention of many geometers, due in part to
-
R. Bamler - Compactness and partial regularity theory of Ricci flows in higher dimensions
BamlerRichard H.We present a new compactness theory of Ricci flows. This theory states that any sequence of Ricci flows that is pointed in an appropriate sense, subsequentially converges to a synthetic flow.
-
P. Burkhardt - Pointwise lower scalar curvature bounds for C0 metrics via regularizing Ricci flow
Burkhardt-GuimPaulaWe propose a class of local definitions of weak lower scalar curvature bounds that is well defined for C0 metrics. We show the following: that our definitions are stable under greater-than-second
-
C. Li - Classifying sufficiently connected PSC manifolds in 4 and 5 dimensions
LiChaoIn this talk, I will discuss some recent developments on the topology of closed manifolds admitting Riemannian metrics of positive scalar curvature. In particular, we will prove if a closed PSC
-
T. Ozuch - Noncollapsed degeneration and desingularization of Einstein 4-manifolds
OzuchTristanWe study the noncollapsed singularity formation of Einstein 4-manifolds. We prove that any smooth Einstein 4-manifold close to a singular one in a mere Gromov-Hausdorff (GH) sense is the result
-
D. Tewodrose - Limits of Riemannian manifolds satisfying a uniform Kato condition
TewodroseDavidPresentation of a joint work with G. Carron and I. Mondello where we study Kato limit spaces.
-
Y. Lai - A family of 3d steady gradient Ricci solitons that are flying wings
LaiYiWe find a family of 3d steady gradient Ricci solitons that are flying wings. This verifies a conjecture by Hamilton. For a 3d flying wing, we show that the scalar curvature does not vanish at
-
A. Mondino - Time-like Ricci curvature bounds via optimal transport
MondinoAndreaThe goal of the talk is to present a recent work in collaboration with Cavalletti (SISSA) on optimal transport in Lorentzian synthetic spaces. The aim is to set up a “Lorentzian analog” of the
