Journée Sous-Riemannienne 2018
Conférences
G. Molino - The Horizontal Einstein Property for H-Type sub-Riemannian Manifolds
We generalize the notion of H-type sub-Riemannian manifolds introduced by Baudoin and Kim, and then introduce a notion of parallel Clifford structure related to a recent work of Moroianu and
Z. Badreddine - Optimal transportation problem and MCP property on sub-Riemannian structures
This presentation is devoted to the study of mass transportation on sub-Riemannian geometry. In order to obtain existence and uniqueness of optimal transport maps, the first relevant method to
D. Prandri - Weyl law for singular Riemannian manifolds
In this talk we present recent results on the asymptotic growth of eigenvalues of the Laplace-Beltrami operator on singular Riemannian manifolds, where all geometrical invariants appearing in
F. Boarotto - Normal forms around regular abnormal curves in rank-two distributions (Part 2)
Let (M, ∆) be a rank-two sub-Riemannian structure on a smooth manifold M, and let x, y be any two points on M. In this talk I will present some recent results concerning the description of the set
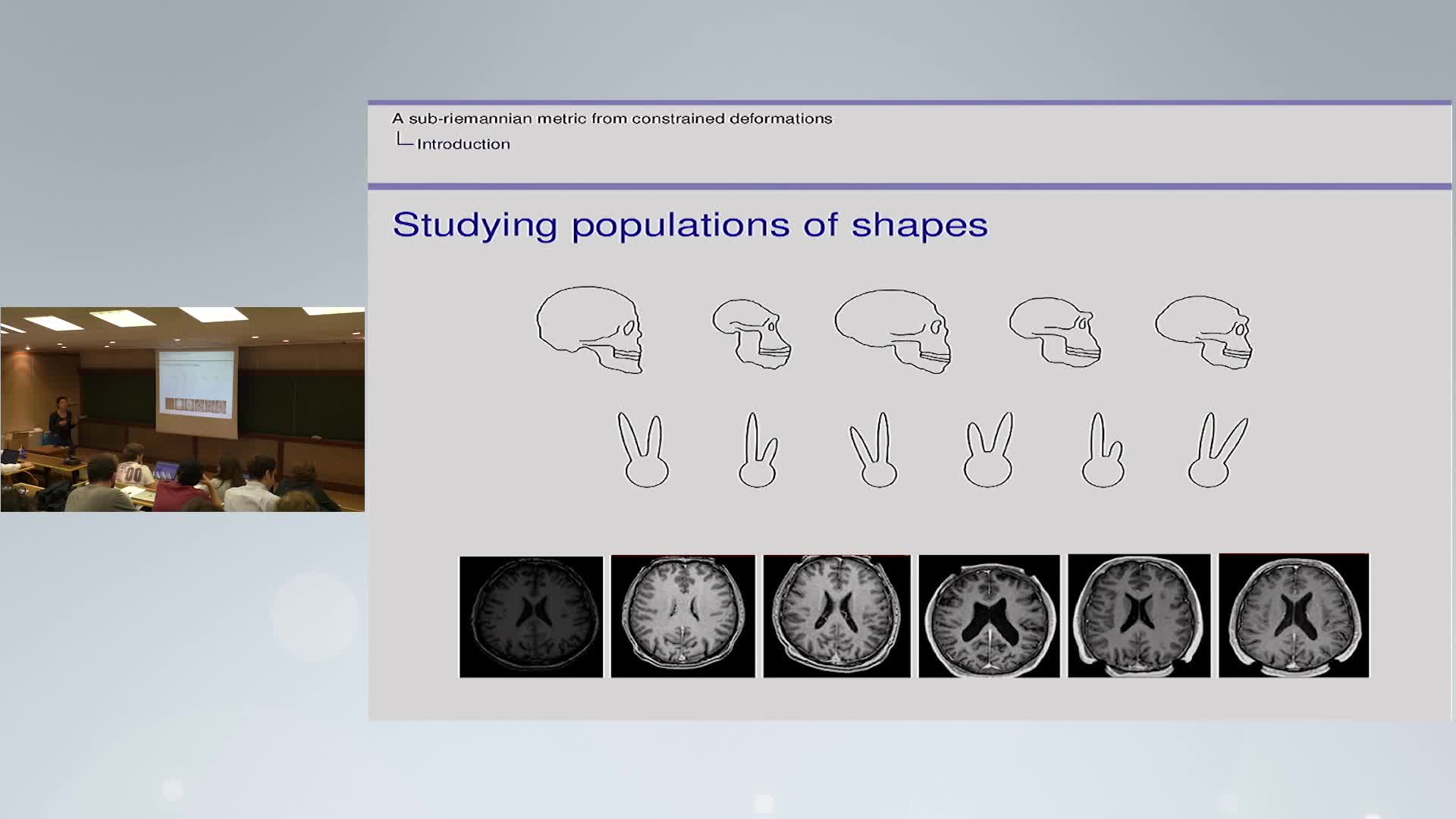
B. Gris - A sub-riemannian metric from constrained deformations
A general method to study a population of objects (images, meshes) is to examine how these objects can be deformed by a chosen class of diffeomorphisms. When these objects satisfy some constraints
D. Vittone - Rectifiability issues in sub-Riemannian geometry
In this talk we discuss two problems concerning “rectifiability” in sub-Riemannian geometry and particularly in the model setting of Carnot groups. The first problem regards the rectifiability of
V. Franceschi - Sub-riemannian soap bubbles
The aim of this seminar is to present some results about minimal bubble clusters in some sub-Riemannian spaces. This amounts to finding the best configuration of m ∈ N regions in a manifold
F. Boarotto - Normal forms around regular abnormal curves in rank-two distributions (Part 1)
Let (M, ∆) be a rank-two sub-Riemannian structure on a smooth manifold M, and let x, y be any two points on M. In this talk I will present some recent results concerning the description of the set
F. Baudoin - Uniform sub-Laplacian comparison theorems on Sasakian manifolds
We will discuss sharp estimates for the sub-Laplacian of a family of distances converging to the sub-Riemannian one. We will deduce results for the sub-Riemannian distance. Uniform measure
Intervenants
Chargé de recherches CNRS au sein du laboratoire des Signaux et Systèmes (Ecole centrale d'électronique, 2017)
Auteur d'une thèse en Mathématiques à Bourgogne Franche-Comté en 2017
Mathématicien, travaillant à l'université du Connecticut (2018)
Ecrit aussi en anglais
Auteur d'une thèse de doctorat en mathématiques soutenue le 12-12-2006 à l'Ecole normale supérieure de Pise
Auteur d'une thèse en Mathématiques appliquées à Paris Saclay en 2016
Chargée de recherche CNRS au Laboratoire Jacques-Louis Lions, Sorbonne Université (en 2023)
Thèse de doctorat en Mathématiques appliquées soutenue en 2002 à l'Université de Paris 7