Ecoles d'été
Collections
2021
FINE Joël
TEWODROSE David
BURKHARDT-GUIM Paula
STERN Daniel
LESOURD Martin
WANG Jian
LAI Yi
LI Chao
SEMOLA Daniele
MONDINO Andrea
BAMLER Richard H.
PERALES Raquel
OZUCH Tristan
SCHULZE Felix
SONG Antoine
LYTCHAK Alexander
SORMANI Christina
RICHARD Thomas
COURTOIS Gilles
BESSON Gérard
CASTILLON Philippe
- niveau 1 niveau 2 niveau 3
- document 1 document 2 document 3
2019
GUENANCIA Henri
HöRING Andreas
DRUEL Stéphane
TOUZET Frédéric
SPICER Calum
NOVIKOV Dmitriĭ Aleksandrovich
MEERSSEMAN Laurent
GHAZOUANI Selim
DEROIN Bertrand
DEMAILLY Jean-Pierre
BINYAMINI Gal
BELOTTO DA SILVA André Ricardo
AMERIK Ekaterina
REIS Helena
POLIZZI Francesco
PEREIRA Jorge Vitório
LORAY Frank
GASBARRI Carlo
FLORIS Enrica
DIVERIO Simone
BOST Jean-Benoît
ARAUJO Carolina
- niveau 1 niveau 2 niveau 3
- document 1 document 2 document 3
2018
ZORICH Anton
YURTTAS Öykü
WRIGHT Alexander
SMILLIE John
SKRIPCHENKO Alexandra
SCHLEIMER Saul
MCMULLEN Curtis Tracy
MATHEUS Carlos
MARMI Stefano
LIECHTI Livio
HUBERT Pascal
FOUGERON Charles
SIMION Filip
DEROIN Bertrand
DAVIS Diana
ARAMAYONA Javier
APISA Paul
CHEN Dawei
PARIS-ROMASKEVICH Olga
SANTHAROUBANE Ramanujan Harischandra
PASQUINELLI Irene
LENZHEN Anna
GUTIéRREZ Rodolfo
ESKIN Alex
WEISS Barak
LEININGER Chris
FORNI Giovanni
- niveau 1 niveau 2 niveau 3
- document 1 document 2 document 3
2017
YUAN Xinyi
TANG Yunqing
PIPPICH Anna-Maria von
LOUGHRAN Daniel
HUANG Zhizhong
SOULé Christophe
SALBERGER Per
PEYRE Emmanuel
GAUDRON Eric
FREIXAS I MONTPLET Gérard
DUJARDIN Romain
CHEN Huayi
CHAMBERT-LOIR Antoine
BRUINIER Jan Hendrik
BURGOS GIL José Ignacio
BOST Jean-Benoît
ANDREATTA Fabrizio
- niveau 1 niveau 2 niveau 3
- document 1 document 2 document 3
2016
MAILLOT Sylvain
LUO Feng
COURTOIS Gilles
MAZET Laurent
KETOVER Daniel
HERSONSKY Sa'Ar
GABAI David
BUZANO Reto
YOUNG Robert Kehoe.
WILKING Burkhard
WALSH G.R.
VIACLOVSKY Jeff
SOUTO CLéMENT Juan
SCHLENKER Jean-Marc
SABOURAU Stéphane
RUPFLIN Melanie
MARKOVIC Vladimir
BELEGRADEK Igor
BEFFARA Vincent
RICHARD Thomas
- niveau 1 niveau 2 niveau 3
- document 1 document 2 document 3
2015
RöGER Matthias
PISANTE Giovanni
WICKRAMASEKARA Neshan
MAGGI Francesco
LIANG Xiangyu
LEONARDI Gian Paolo
KIRCHHEIM Bernd
GIACOMINI Alessandro
DE LELLIS Camillo
FU Joseph H. G.
TORO Tatiana
TONEGAWA Yoshihiro
DAVID Guy
ALIKAKOS Nicholas D.
ALBERTI Giovanni
BRAIDES Andrea
- niveau 1 niveau 2 niveau 3
- document 1 document 2 document 3
2014
STROHMAIER Alexander
ZWORSKI Maciej
JOUDIOUX Jérémie
KLAINERMAN Sergiu
LEFLOCH Philippe G.
MASON Lionel J.
DYATLOV Semyon
DAPPIAGGI Claudio
DAFERMOS Mihalis
BLUE Pieter
BACKDAHL Thomas
BACHELOT Alain
VASY András
SZEFTEL Jérémie
GOVER Ashwin Roderick
GéRARD Christian
ANDERSSON Lars
- niveau 1 niveau 2 niveau 3
- document 1 document 2 document 3
2013
LIARDET Pierre
GORODNIK Alexander
POLLICOTT Mark
VERGER-GAUGRY Jean-Louis
FROUGNY Christiane
DURAND Fabien
DAJANI Karma
BOYLE Mike
BERTIN Marie-José
BERTHé Valérie
- niveau 1 niveau 2 niveau 3
- document 1 document 2 document 3
2012
VITERBO Claude
TELEMAN Andrei
LALONDE François
SUKHOV Alexandre
IVACHKOVITCH Sergueï
DUVAL Julien
DEMAILLY Jean-Pierre
CERVEAU Dominique
FORSTNERIč Franc
- niveau 1 niveau 2 niveau 3
- document 1 document 2 document 3
2011
LEE Yuan-Pin
MAULIK Davesh
PERRIN Nicolas
MANN Etienne
MANIVEL Laurent
PIXTON Aaron
PANDHARIPANDE Rahul
MULASE Motohico
CHIODO Alessandro
- niveau 1 niveau 2 niveau 3
- document 1 document 2 document 3
Cours
Phong NGUYEN - Recent progress on lattices's computations 2
This is an introduction to the mysterious world of lattice algorithms, which have found many applications in computer science, notably in cryptography. We will explain how lattices are represented by
Aurel PAGE - Cohomology of arithmetic groups and number theory: geometric, asymptotic and computati…
In this lecture series, the first part will be dedicated to cohomology of arithmetic groups of lower ranks (e.g., Bianchi groups), their associated geometric models (mainly from hyperbolic geometry)
Alexander HULPKE - Computational group theory, cohomology of groups and topological methods 5
The lecture series will give an introduction to the computer algebra system GAP, focussing on calculations involving cohomology. We will describe the mathematics underlying the algorithms, and how to
Alexander HULPKE - Computational group theory, cohomology of groups and topological methods 4
The lecture series will give an introduction to the computer algebra system GAP, focussing on calculations involving cohomology. We will describe the mathematics underlying the algorithms, and how to
Gabriele NEBE - Lattices, Perfects lattices, Voronoi reduction theory, modular forms, computations …
The talks of Coulangeon will introduce the notion of perfect, eutactic and extreme lattices and the Voronoi's algorithm to enumerate perfect lattices (both Eulcidean and Hermitian). The talk of Nebe
Oussama Hamza - Hilbert series and mild groups
Let $p$ be an odd prime number and $G$ a finitely generated pro-$p$ group. Define $I(G)$ the augmentation ideal of the group algebra of $G$ over $F_p$ and define the Hilbert series of $G$ by: $G(t):
Tobias Moede - Coclass theory for nilpotent associative algebras
The coclass of a finite p-group of order p^n and class c is defined as n-c. Using coclass as the primary invariant in the investigation of finite p-groups turned out to be a very fruitful approach.
Zachary Himes - On not the rational dualizing module for $\text{Aut}(F_n)$
Bestvina--Feighn proved that $\text{Aut}(F_n)$ is a rational duality group, i.e. there is a $\mathbb{Q}[\text{Aut}(F_n)]$-module, called the rational dualizing module, and a form of Poincar\'e duality
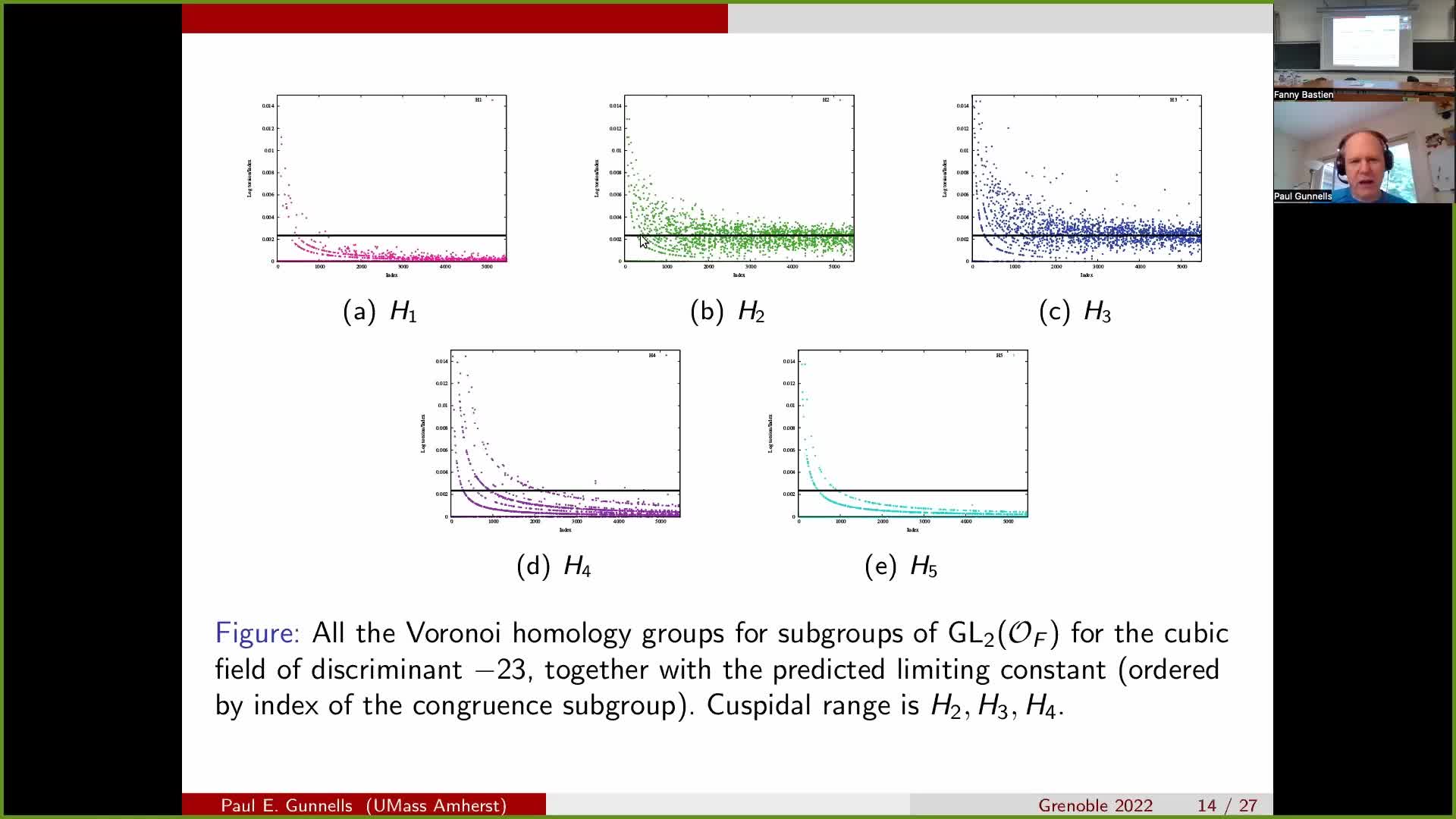
Paul GUNNELLS - Cohomology of arithmetic groups and number theory: geometric, asymptotic and comput…
In this lecture series, the first part will be dedicated to cohomology of arithmetic groups of lower ranks (e.g., Bianchi groups), their associated geometric models (mainly from hyperbolic geometry)
Paul GUNNELLS - Cohomology of arithmetic groups and number theory: geometric, asymptotic and comput…
In this lecture series, the first part will be dedicated to cohomology of arithmetic groups of lower ranks (e.g., Bianchi groups), their associated geometric models (mainly from hyperbolic geometry)
Paul GUNNELLS - Cohomology of arithmetic groups and number theory: geometric, asymptotic and comput…
In this lecture series, the first part will be dedicated to cohomology of arithmetic groups of lower ranks (e.g., Bianchi groups), their associated geometric models (mainly from hyperbolic geometry)
Paul GUNNELLS - Cohomology of arithmetic groups and number theory: geometric, asymptotic and comput…
In this lecture series, the first part will be dedicated to cohomology of arithmetic groups of lower ranks (e.g., Bianchi groups), their associated geometric models (mainly from hyperbolic geometry)
Conférences
Lewis Combes - Computing Selmer groups attached to mod p Galois representations
Selmer groups attached to a p-adic Galois representation have been studied thoroughly, but their mod p cousins have so far received less attention. In this talk we explain the construction of the p
Petru Constantinescu - On the distribution of modular symbols and cohomology classes
Motivated by a series of conjectures of Mazur, Rubin and Stein, the study of the arithmetic statistics of modular symbols has received a lot of attention in recent years. In this talk, I will
Kieran Child - Computation of weight 1 modular forms
A major achievement of modern number theory is the proof of a bijection between odd, irreducible, 2-dimensional Artin representations and holomorphic weight 1 Hecke eigenforms. Despite this result,
Tobias Braun - Orthogonal Determinants
Basic concepts and notions of orthogonal representations are introduced. If X : G → GL(V ) is a K-representation of a nite group G it may happen that its image X(G) xes a nondegenerate quadratic
Benjamin Brück - High-dimensional rational cohomology ...
By a result of Church-Putman, the rational cohomology of $\operatorname{SL}_n(\mathbb{Z})$ vanishes in "codimension one", i.e. $H^{{n \choose 2} -1}(\operatorname{SL}_n(\mathbb{Z});\mathbb{Q}) = 0$
Intervenants
Informaticien. Directeur de recherche INRIA, équipe Conception et analyse de systèmes pour la confidentialité et l'authentification de données et d'entités (CASCADE), Département d'informatique de l'ENS-PSL (DI-ENS, UMR 8548), École normale supérieure, Paris (en 2023)
Doctorat en sciences et techniques (Université de Paris VII, 1999)
Auteur d'une thèse en Mathematiques à Bordeaux en 2014
Mathématicienne. En poste : Lehrstuhl D für Mathematik, Technische Hochschule Aachen, Allemagne (en 2006). Professeure à l'Université d'Aix-la-Chapelle (RWTH Aachen University), Allemagne (en 2022)
Mathématicien. Professeur associé à l'Université de Massachusett (Etats-Unis) en 2007.