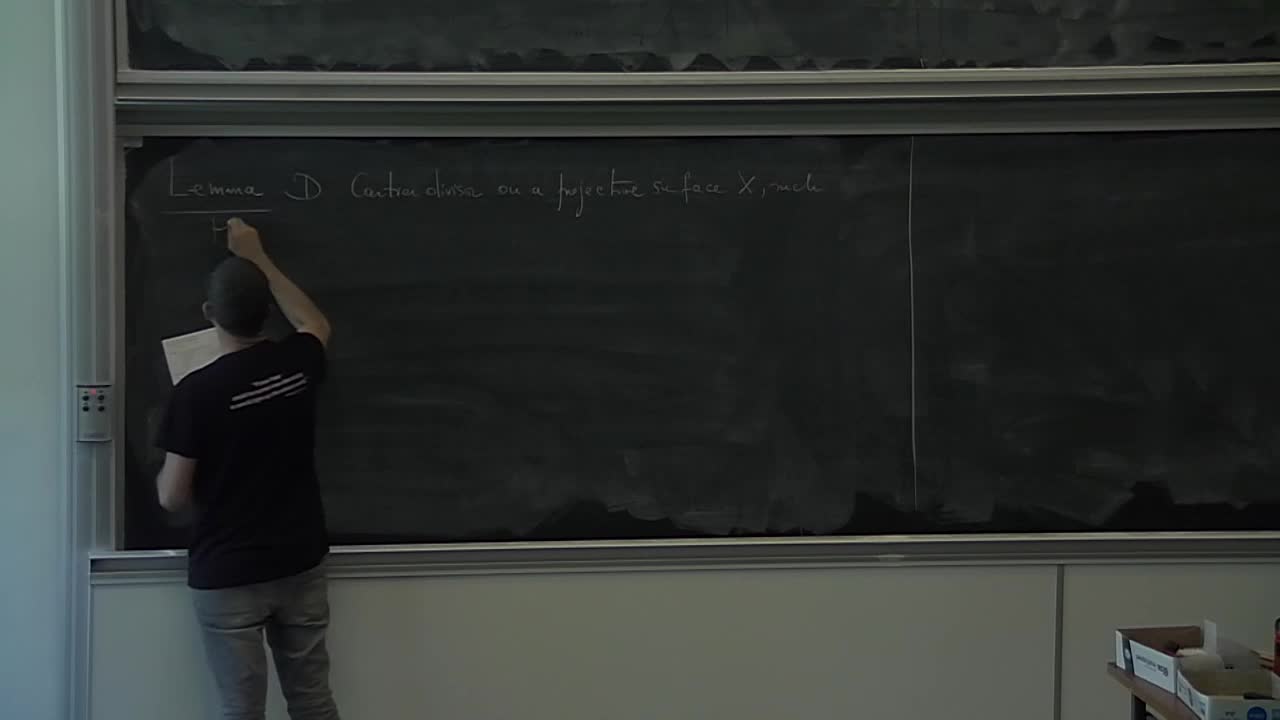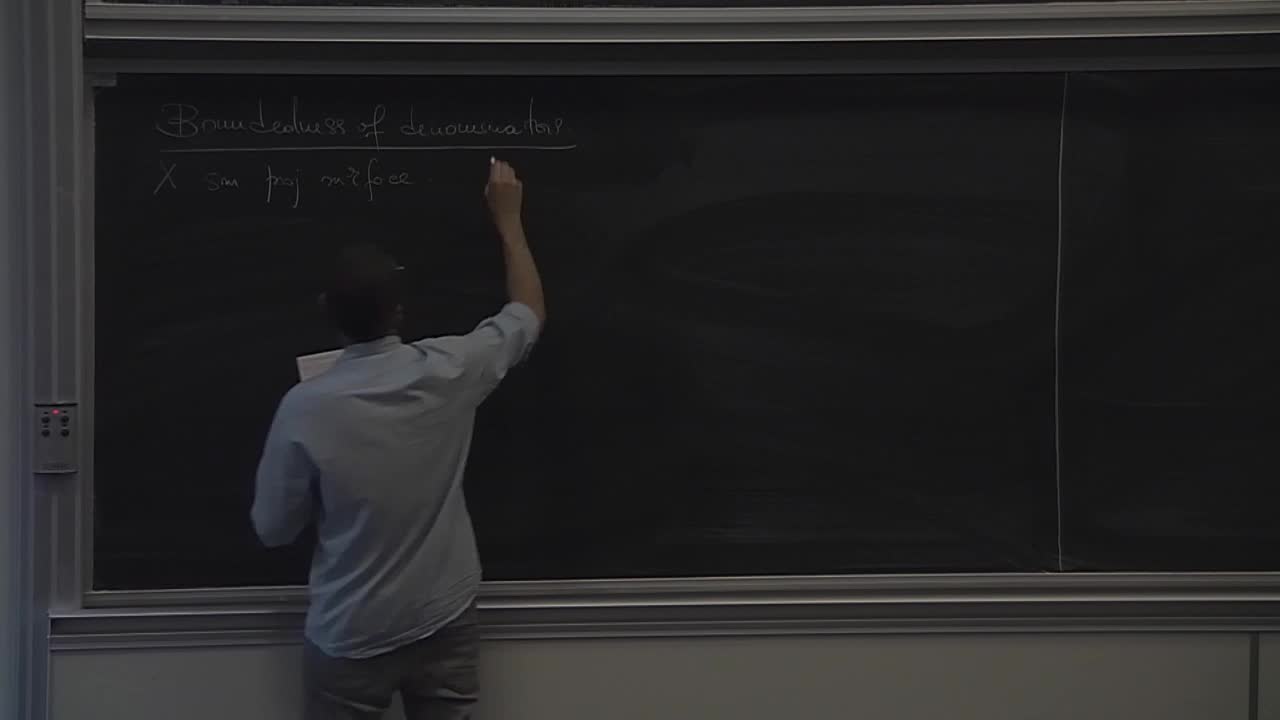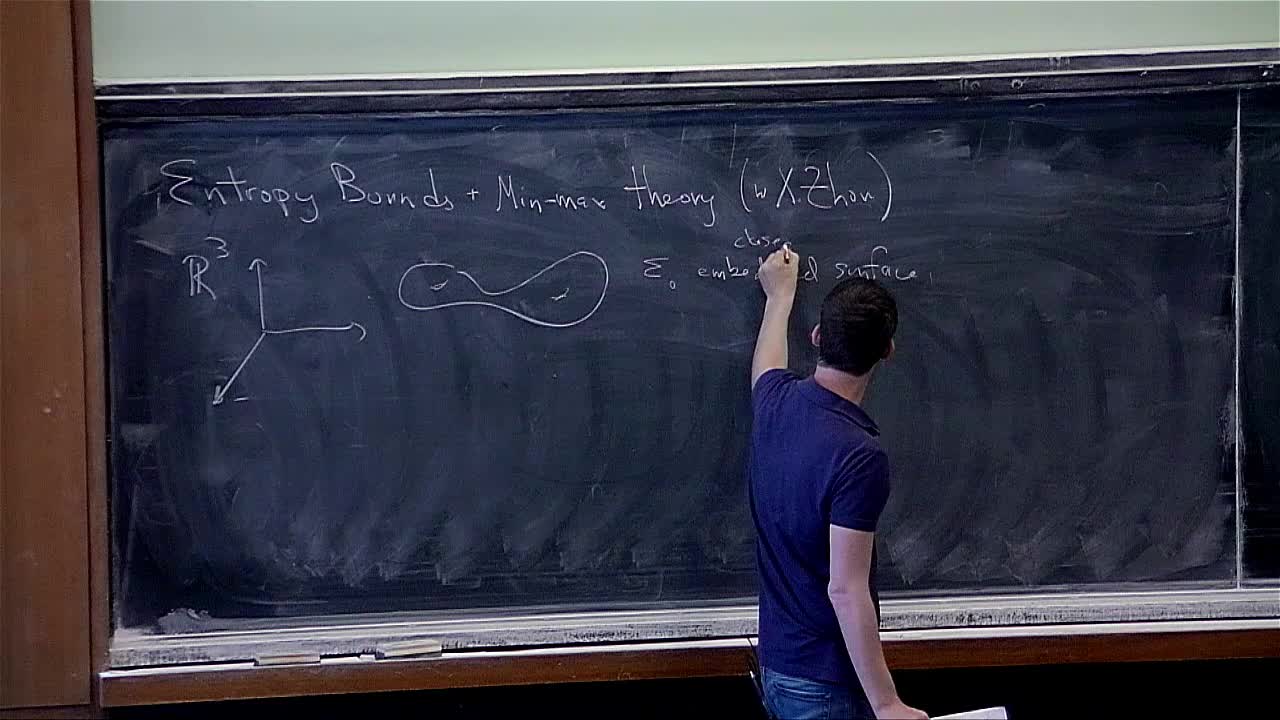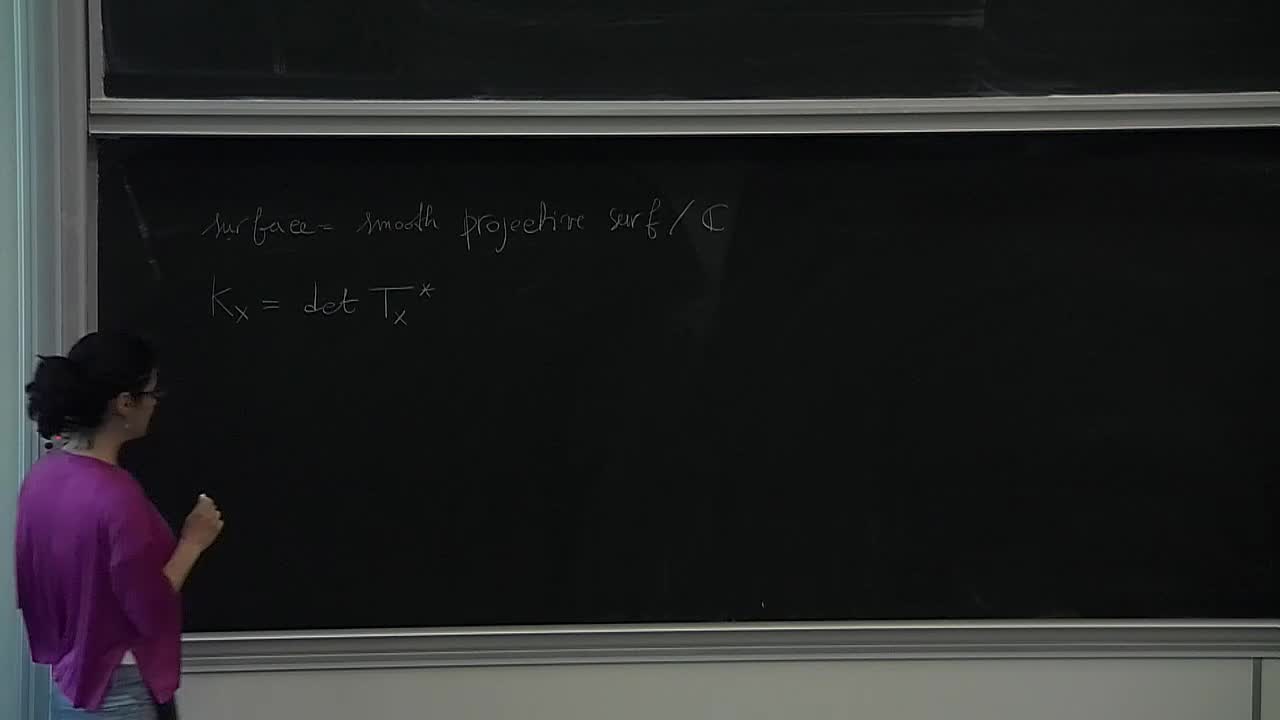Surfaces

Objets singuliers ou l’inattendu en arts et sciences

We give a summary of the Minimal Model Program (namely, Mori Theory) in the case of surfaces.

We give a summary of the Minimal Model Program (namely, Mori Theory) in the case of surfaces.

L'Espagne, depuis l'époque romaine, a connu un développement de sa castanéiculture proche du modèle français. Aujourd'hui, sa production est supérieure à la production française en termes de volumes.

Le châtaignier et son fruit, la châtaigne, représentent une culture de grande importance dans l'économie portugaise. Le Portugal prétend augmenter ses aires de plantation du châtaignier à l'horizon

A travers cet entretien filmé, le professeur José Gomes-Laranjo nous explique le projet RefCast, qui est la contraction, en portugais, de Reforço e Castanha (Renfort et Châtaigne). Cette idée de

Our recent joint work with D. Gu established a discrete version of the uniformization theorem for compact polyhedral surfaces.   In this talk, we prove that discrete uniformizaton maps converge to

An old theorem of Huber asserts that the number of closed geodesics of length at most L on a hyperbolic surface is asymptotic to $\frac{e^L}L$. However, things are less clear if one either fixes the

In 2012, Colding-Ilmanen-Minicozzi-White conjectured that the entropy of any closed surface in R^3 is at least that of the self-shrinking two-sphere. I will explain joint work with X. Zhou where we

The goal of this minicourse is to introduce MMP for foliations on surfaces and to outline the classification of foliations on projective surfaces up to birational equivalence.

The goal of this minicourse is to introduce MMP for foliations on surfaces and to outline the classification of foliations on projective surfaces up to birational equivalence.

The goal of this minicourse is to introduce MMP for foliations on surfaces and to outline the classification of foliations on projective surfaces up to birational equivalence.