PSL Summer School on High Dimensional Probability and Algorithms - HDPA 2019
Description
This one week summer school belongs to the PSL-maths program of the PSL university. It is devoted to High dimensional probability and algorithms. The targeted audience is young and less young mathematicians starting from the PhD level. The school took place in ÉNS Paris, from July 1 to 5, 2019.
This school is supported by PSL, CNRS, CEREMADE, ÉNS, and IUF. The organizers are Claire Boyer (Sorbonne Université & ÉNS), Djalil Chafaï (Paris-Dauphine/PSL), and Joseph Lehec (Paris-Dauphine/PSL & ÉNS/PSL).
The program consists in two 9-hour courses:
Sébastien Bubeck (Microsoft Research)
Some geometric aspects of randomized online decision making.
Joel Tropp (California Institute of Technology)
Random matrix theory and computational linear algebra.
Six 45-minute talks:
Yohann De Castro (École des Ponts)
Spectral convergence of random graphs and a focus on random geometric graphs.
Alexandra Carpentier (U. Potsdam)
Introduction to some problems of composite and minimax hypothesis testing.
Olga Klopp (ESSEC / CREST)
Sparse Network Estimation.
Laurent Massoulié, (INRIA/Microsoft)
Planting trees in graphs, and finding them back.
Nicolas Verzelen (INRA)
Clustering with the relaxed K-means.
Lenka Zdeborova (CNRS / CEA Saclay)
Loss landscape and behaviour of algorithms in the spiked matrix-tensor model.
More information on https://hdpa2019.sciencesconf.org/
The video capture was produced technically by Thierry Bohnke and Marianne Herve from OHNK.
Cours/Séminaire
Tropp 9/9 - Random matrix theory and computational linear algebra
Tropp
Joel Aaron
This course treats some contemporary algorithms from computational linear algebra that involve random matrices. Rather than surveying the entire field, we focus on a few algorithms that are both
Tropp 8/9 - Random matrix theory and computational linear algebra
Tropp
Joel Aaron
This course treats some contemporary algorithms from computational linear algebra that involve random matrices. Rather than surveying the entire field, we focus on a few algorithms that are both
Tropp 7/9 - Random matrix theory and computational linear algebra
Tropp
Joel Aaron
This course treats some contemporary algorithms from computational linear algebra that involve random matrices. Rather than surveying the entire field, we focus on a few algorithms that are both
Tropp 6/9 - Random matrix theory and computational linear algebra
Tropp
Joel Aaron
This course treats some contemporary algorithms from computational linear algebra that involve random matrices. Rather than surveying the entire field, we focus on a few algorithms that are both
Bubeck 9/9 - Some geometric aspects of randomized online decision making
Bubeck
Sébastien
This course is concerned with some of the canonical non-stochastic models of online decision making. These models have their origin in works from the 1950's and 1960's, and went through a resurgence
Bubeck 8/9 - Some geometric aspects of randomized online decision making
Bubeck
Sébastien
This course is concerned with some of the canonical non-stochastic models of online decision making. These models have their origin in works from the 1950's and 1960's, and went through a resurgence
Bubeck 5/9 - Some geometric aspects of randomized online decision making
Bubeck
Sébastien
This course is concerned with some of the canonical non-stochastic models of online decision making. These models have their origin in works from the 1950's and 1960's, and went through a resurgence
Bubeck 7/9 - Some geometric aspects of randomized online decision making
Bubeck
Sébastien
This course is concerned with some of the canonical non-stochastic models of online decision making. These models have their origin in works from the 1950's and 1960's, and went through a resurgence
Tropp 5/9 - Random matrix theory and computational linear algebra
Tropp
Joel Aaron
This course treats some contemporary algorithms from computational linear algebra that involve random matrices. Rather than surveying the entire field, we focus on a few algorithms that are both
Bubeck 6/9 - Some geometric aspects of randomized online decision making
Bubeck
Sébastien
This course is concerned with some of the canonical non-stochastic models of online decision making. These models have their origin in works from the 1950's and 1960's, and went through a resurgence
Tropp 3/9 - Random matrix theory and computational linear algebra
Tropp
Joel Aaron
This course treats some contemporary algorithms from computational linear algebra that involve random matrices. Rather than surveying the entire field, we focus on a few algorithms that are both
Bubeck 3/9 - Some geometric aspects of randomized online decision making
Bubeck
Sébastien
This course is concerned with some of the canonical non-stochastic models of online decision making. These models have their origin in works from the 1950's and 1960's, and went through a resurgence
Conférence
Carpentier - Introduction to some problems of composite and minimax hypothesis testing
Carpentier
Alexandra
A fundamental question in statistics is: how well can we fulfil a given aim given the data that one possesses? Answering this question sheds light on the possibilities, but also on the fundamental
Zdeborová - Loss landscape and behaviour of algorithms in the spiked matrix-tensor model
Zdeborová
Lenka
A key question of current interest is: How are properties of optimization and sampling algorithms influenced by the properties of the loss function in noisy high-dimensional non-convex settings?
Massoulié - Planting trees in graphs, and finding them back
Massoulié
Laurent
In this talk we consider detection and reconstruction of planted structures in Erdős-Rényi random graphs.
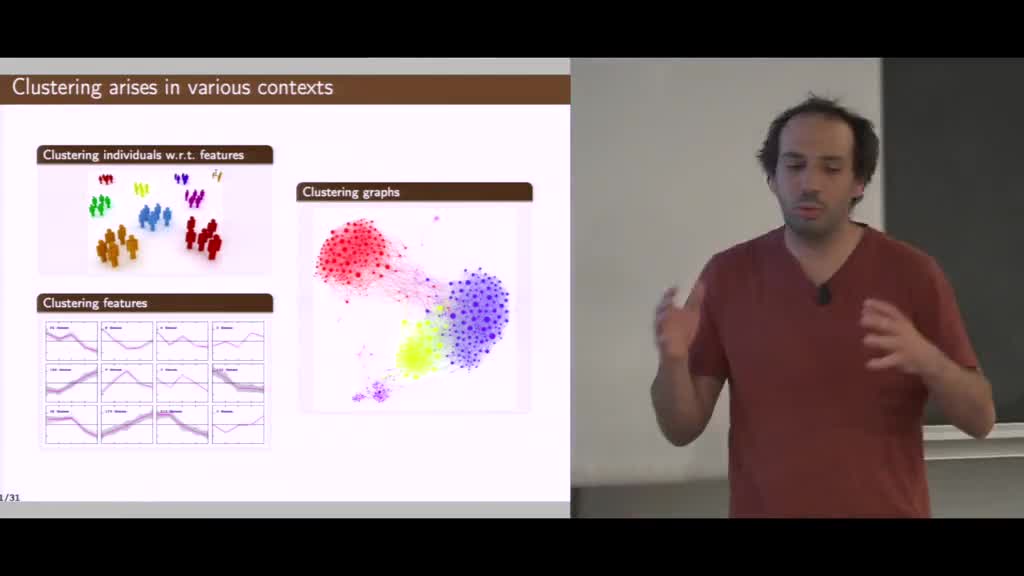
Verzelen - Clustering with the relaxed K-means
Verzelen
Nicolas
This talk is devoted to clustering problems. It amounts to partitionning a set of given points or the nodes of a given graph, in such a way that the groups are as homogeneous as possible. After
Klopp - Sparse Network Estimation
Klopp
Olga
Inhomogeneous random graph models encompass many network models such as stochastic block models and latent position models. We consider the problem of the statistical estimation of the matrix of
De Castro - Spectral convergence of random graphs and a focus on random geometric graphs
Castro
Yohann de
In this talk, we present a non-asymptotic bound on the L2 distance between the spectrum of the probability matrix of a random graph and the spectrum of the integral operator. Then, we study the random
Intervenants
France
Titulaire d'un doctorat en Mathématiques (Lille 1, 2010)
Professeur adjoint à l'université de Princeton, département de la recherche opérationnelle et de l'ingénierie financière
France
Allemagne
Mathématicienne. Professeure, responsable de l'équipe Mathematical statistics and machine learning, Institut für Mathematik, Universität Potsdam (2024)
Titulaire d'un doctorat en Mathématiques appliquées. Informatique (Lille 1, 2012)
Membre du jury d'une thèse en Mathématiques à Université Côte d'Azur en 2025
Tchéquie
France
ZZ
Physicienne. Professeure associée, directrice du Laboratoire de physique statistique des systèmes computationnels - Statistical physics of computation laboratory (SPOC), Institut de physique (IPHYS), École polytechnique fédérale, Lausanne, Suisse (2024)
Doctorat en physique théorique (Paris 11 en cotutelle avec Universita Karlova v Praze, 2008)
Médaille de bronze du CNRS 2018