Notice
Fast Polynomial Evaluation (présentation + demo)
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
The FPE algorithm is backed by a mathematical result on the parcimonious representation of
polynomials. Our article [1] contains a detailed analysis of the complexity and a full error analysis,
which guarantees that the algorithm performs as well as H¨orner’s scheme, only faster. Our algorithm is
implemented in a companion library, written in standard C and released as an open-source project [2].
Our claims regarding complexity and accuracy are confirmed in practice by a set of comprehensive
benchmarks.
This work is a spin-off in a general research program regarding high-degree polynomials and new
numerical methods for complex dynamics. During JCAD 2021 [3], we had presented the successful
splitting of a polynomial of degree 1012, that is of interest for the study of the Mandelbrot set.
In a 20 minutes talk, we would like to present the FPE algorithm. The underlying principles (lazy
addition and a geometric selection principle based on convexity) are simple enough and can be of interest
to a wide audience. No technical mathematical background is required. We will also explain how we
used the infrastructure of the HPC Center Romeo (Reims) to perform systematic benchmarks
References
[1] R. Anton, N. Mihalache, F. Vigneron. Fast evaluation of real and complex polynomials. Preprint
2022, HAL-03820369 / arXiv:2211.06320.
[2] N. Mihalache, F. Vigneron. FPE library : https://github.com/fvigneron/FastPolyEval.
[3] N. Mihalache, F. Vigneron. How to split a tera-polynomial. In preparation.
Intervention / Responsable scientifique
Thème
Documentation
Dans la même collection
-
Table ronde et discussions : infrastructures de calcul et ateliers de la donnée de recherche Data G…
CastexStéphanieRenardArnaudAlbaretLucieRenonNicolasDufayardJean-FrançoisPARTIE 2 : Les ateliers de la données
-
Table ronde et discussions : infrastructures de calcul et ateliers de la donnée de recherche Data G…
CastexStéphanieRenardArnaudAlbaretLucieRenonNicolasDufayardJean-FrançoisPARTIE 7 : Conclusion
-
Table ronde et discussions : infrastructures de calcul et ateliers de la donnée de recherche Data G…
CastexStéphanieRenardArnaudAlbaretLucieRenonNicolasDufayardJean-FrançoisPARTIE 4 : Des interactions croisées, liens entre le calcul et les données.
-
Table ronde et discussions : infrastructures de calcul et ateliers de la donnée de recherche Data G…
CastexStéphanieRenardArnaudAlbaretLucieRenonNicolasDufayardJean-FrançoisPARTIE 1 : Introduction et présentation des intervenants
-
Table ronde et discussions : infrastructures de calcul et ateliers de la donnée de recherche Data G…
CastexStéphanieRenardArnaudAlbaretLucieRenonNicolasDufayardJean-FrançoisPARTIE 6 : L'accompagnement autour de la gestion des données
-
Table ronde et discussions : infrastructures de calcul et ateliers de la donnée de recherche Data G…
CastexStéphanieRenardArnaudAlbaretLucieRenonNicolasDufayardJean-FrançoisPARTIE 3 : les liens entre les structures
-
Table ronde et discussions : infrastructures de calcul et ateliers de la donnée de recherche Data G…
CastexStéphanieRenardArnaudAlbaretLucieRenonNicolasDufayardJean-FrançoisPARTIE 5 : Des interactions croisées, à propos des compétences
-
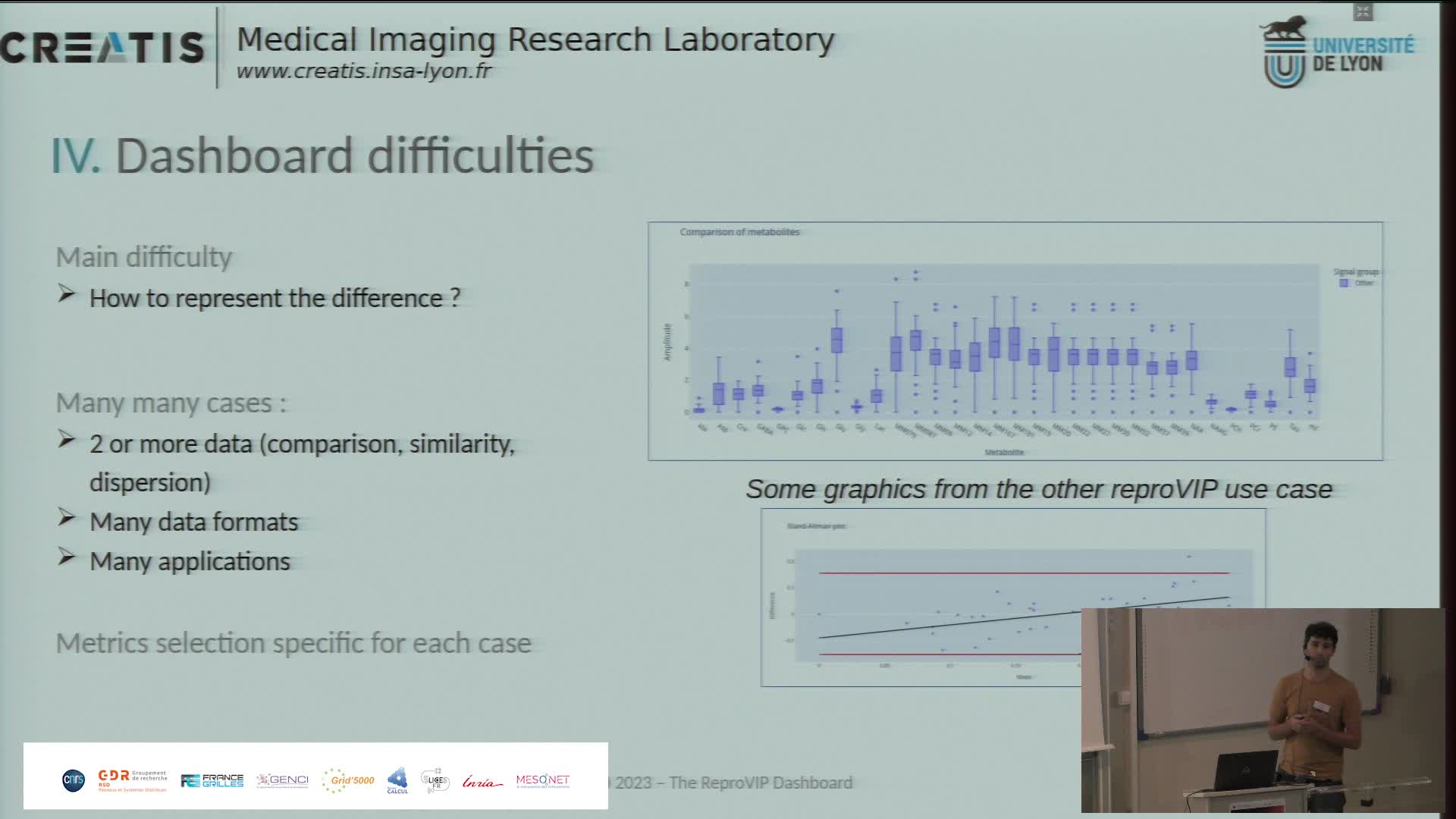
Présentation du dashboard ReproVIP pour visualiser la reproductibilité dans l'imagerie médicale
BonnetAxelLa plateforme d'imagerie virtuelle VIP [1] (https://vip.creatis.insa-lyon.fr) est un portail web de simulation et d'analyse d'images médicales. Elle existe depuis plus de 10 ans et a évolué pour
-
Parallélisation par l'intermédiaire d'une fenêtre à mémoire partagée (MPI 3.0) : application à un c…
ElyakimePierreJADIM est un code de calcul de mécanique des fluides développé en Fortran 90 à l'Institut de Mécanique des Fluides de Toulouse (IMFT).
-
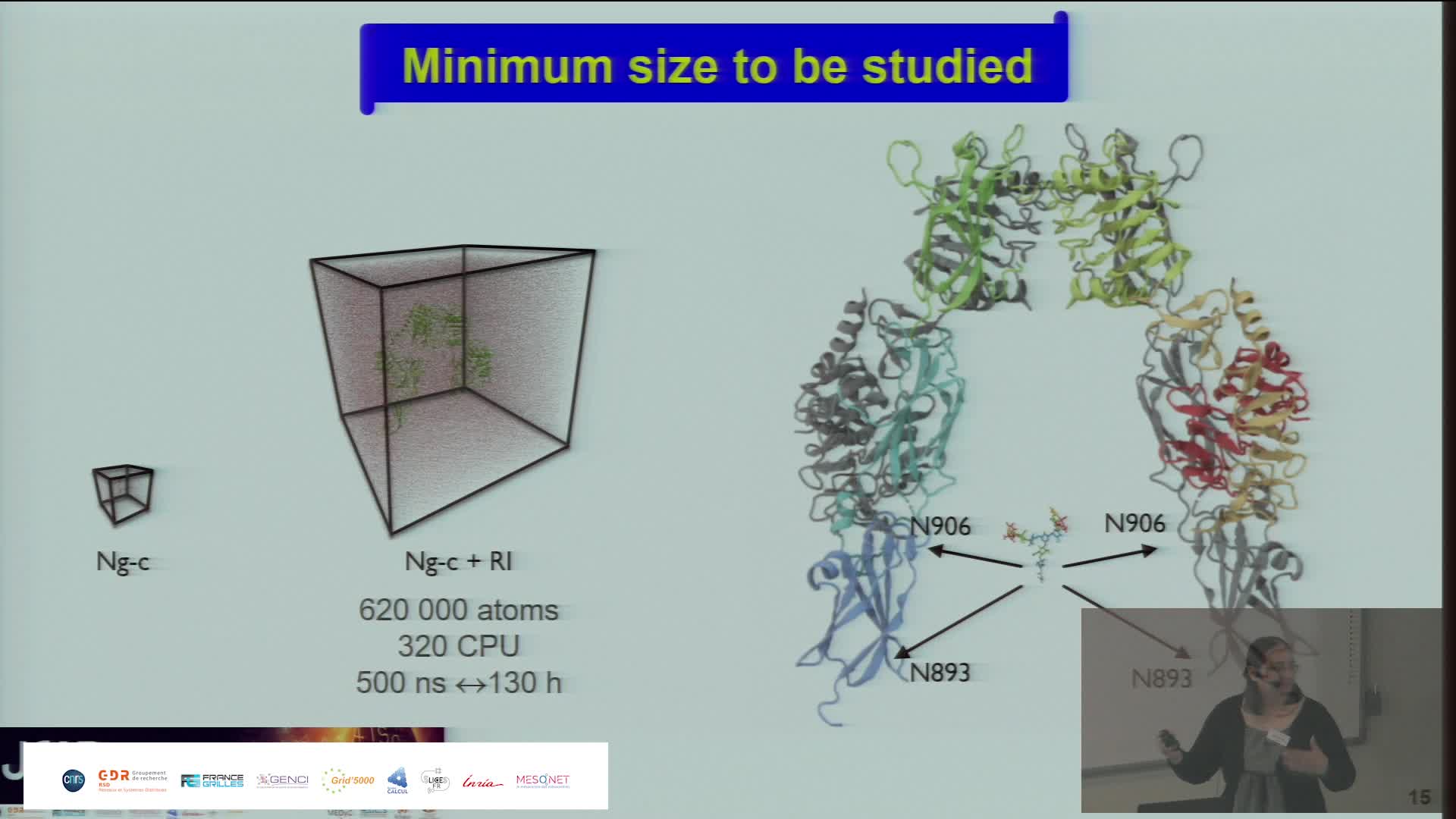
Simulating the Extra Cellular Matrix - Calculations and data from atom to animal
BaudStéphanieThe extracellular matrix (ECM) is a three-dimensional network of macromolecules that is the architectural support for cells and allows tissue cohesion. This dynamic structure regulates many biological
-
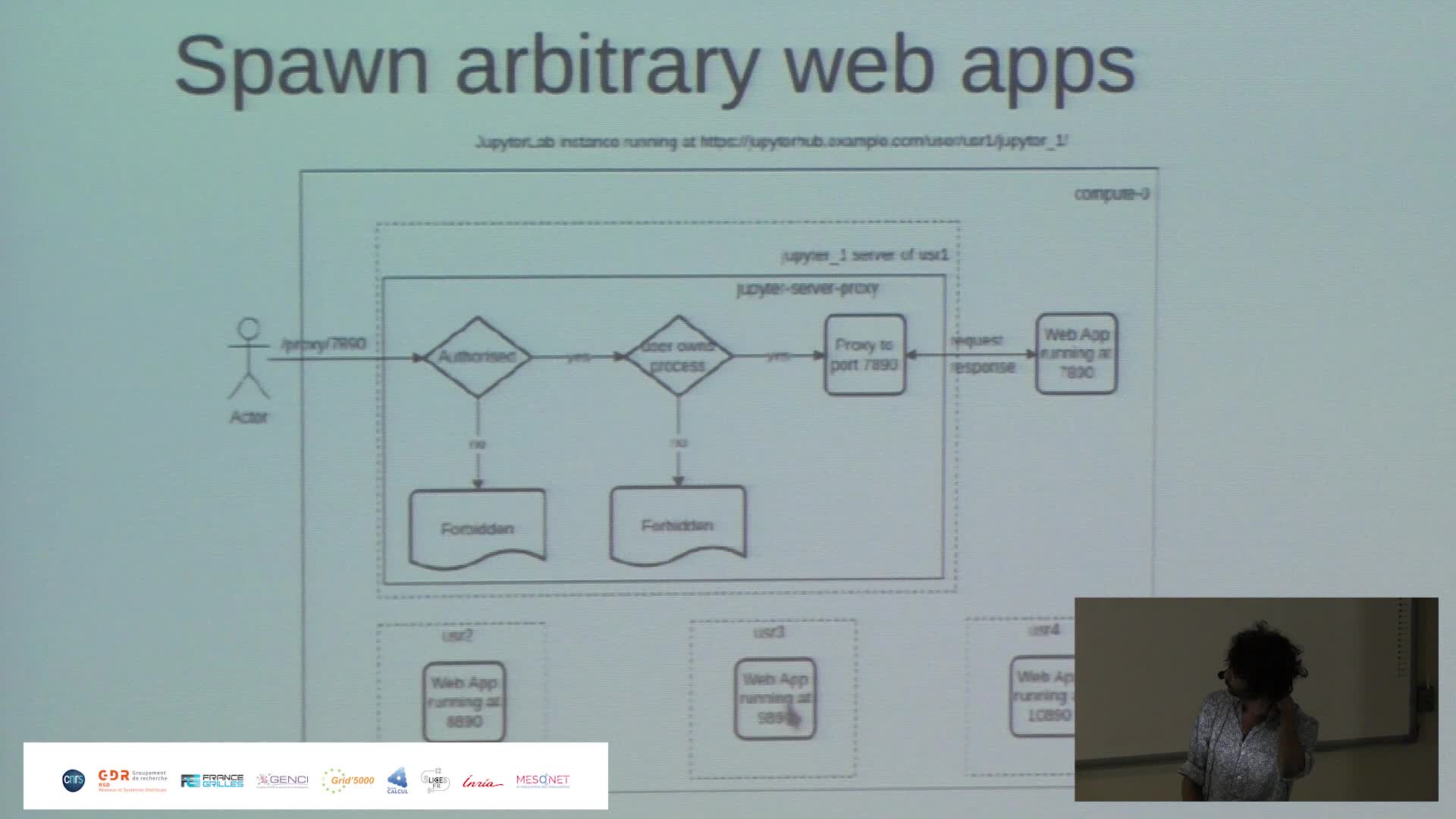
Harnessing the power of Jupyter{Hub,Lab} to make Jean Zay HPC resources more accessible
PaipuriMahendraThis talk revolves around the deployment of JupyterHub on Jean Zay HPC platform and how it is done to meet the demands of RSSI (ZRR constraints) and also to provide a seamless experience to the end
-
Using High Performance Computing to decipher the impact of ageing process on collagens
DepenveillerCamillePlant cells have to face environmental stress, and in this context, being able to decipher the organization of the plant plasma membrane is a key point to better understand this adaptability of plasma