Richard, Thomas (1985-.... ; auteur en mathématiques)
- Mathématiques
- Grenoble
- eem2021
- contraintes de courbures et espaces métriques
- curvature constraints and spaces of metrics
- Riemannian geometry
- Grenoble
- eem2021
- contraintes de courbures et espaces métriques
- curvature constraints and spaces of metrics
- Riemannian geometry
- Grenoble
- eem2021
- contraintes de courbures et espaces métriques
- curvature constraints and spaces of metrics
Vidéos
T. Richard - Advanced basics of Riemannian geometry 1
We will present some of the tools used by the more advanced lectures. The topics discussed will include : Gromov Hausdorff distance, comparison theorems for sectional and Ricci curvature, the
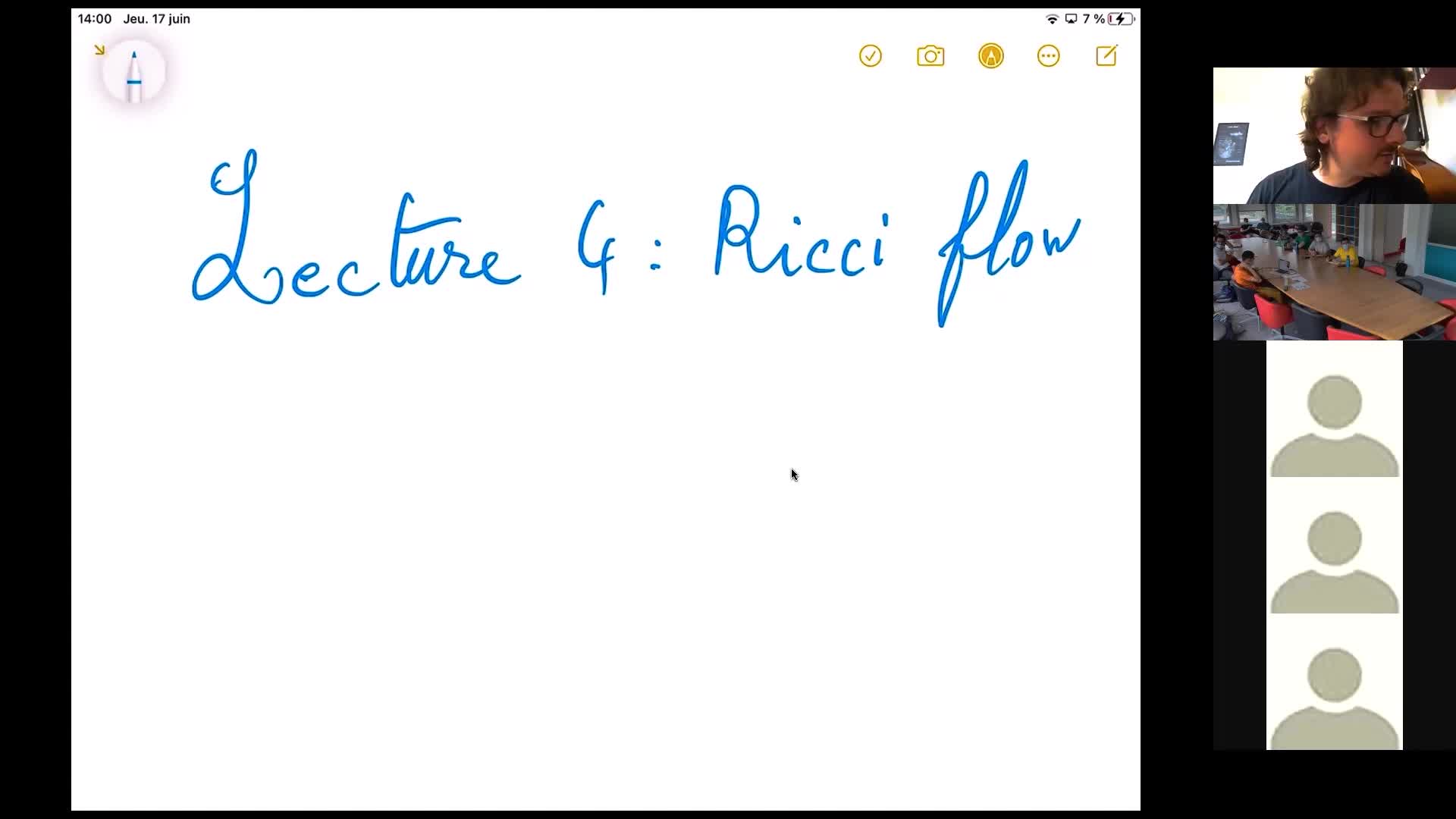
T. Richard - Advanced basics of Riemannian geometry 4
We will present some of the tools used by the more advanced lectures. The topics discussed will include : Gromov Hausdorff distance, comparison theorems for sectional and Ricci curvature, the
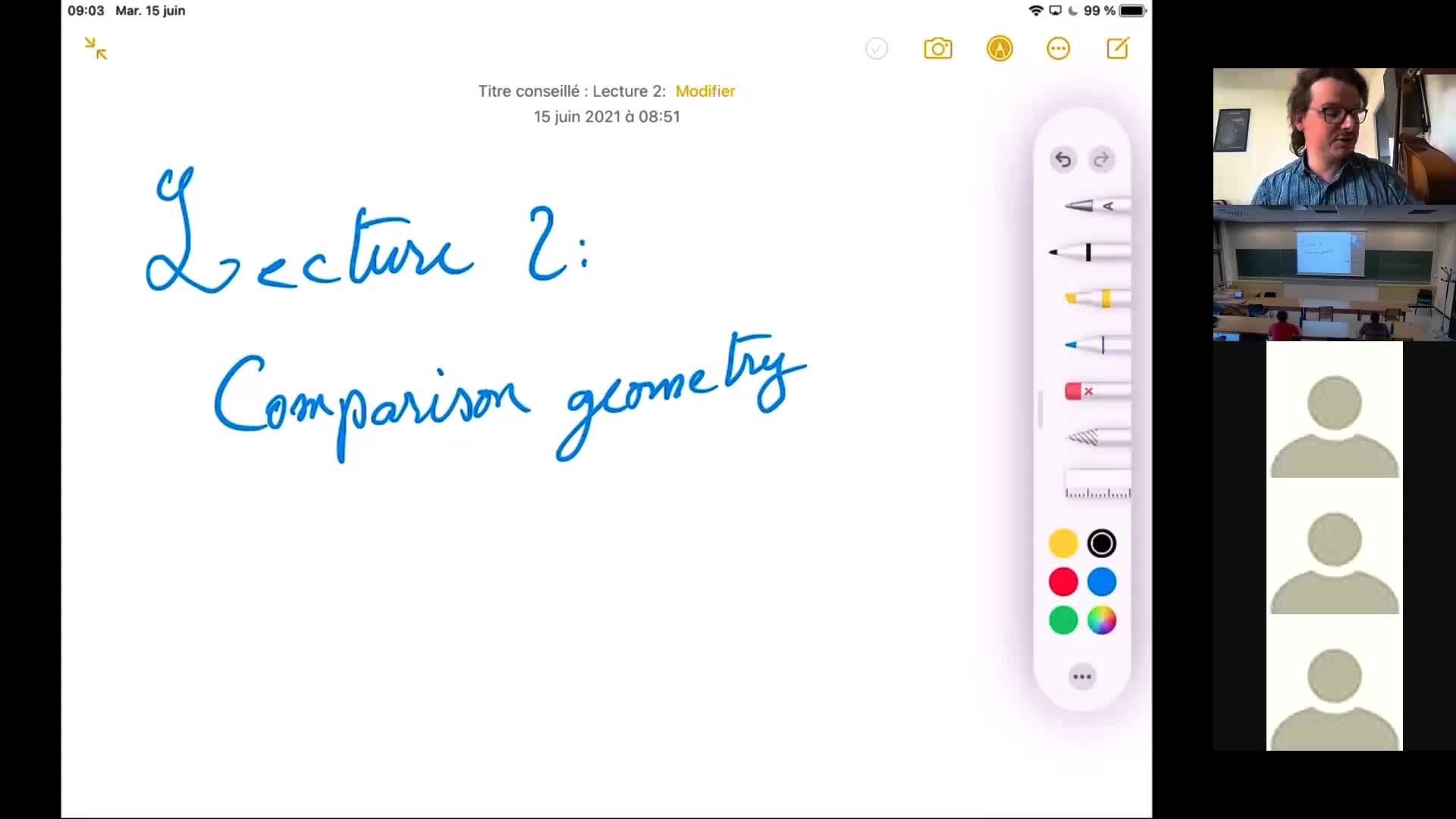
T. Richard - Advanced basics of Riemannian geometry 2
We will present some of the tools used by the more advanced lectures. The topics discussed will include : Gromov Hausdorff distance, comparison theorems for sectional and Ricci curvature, the
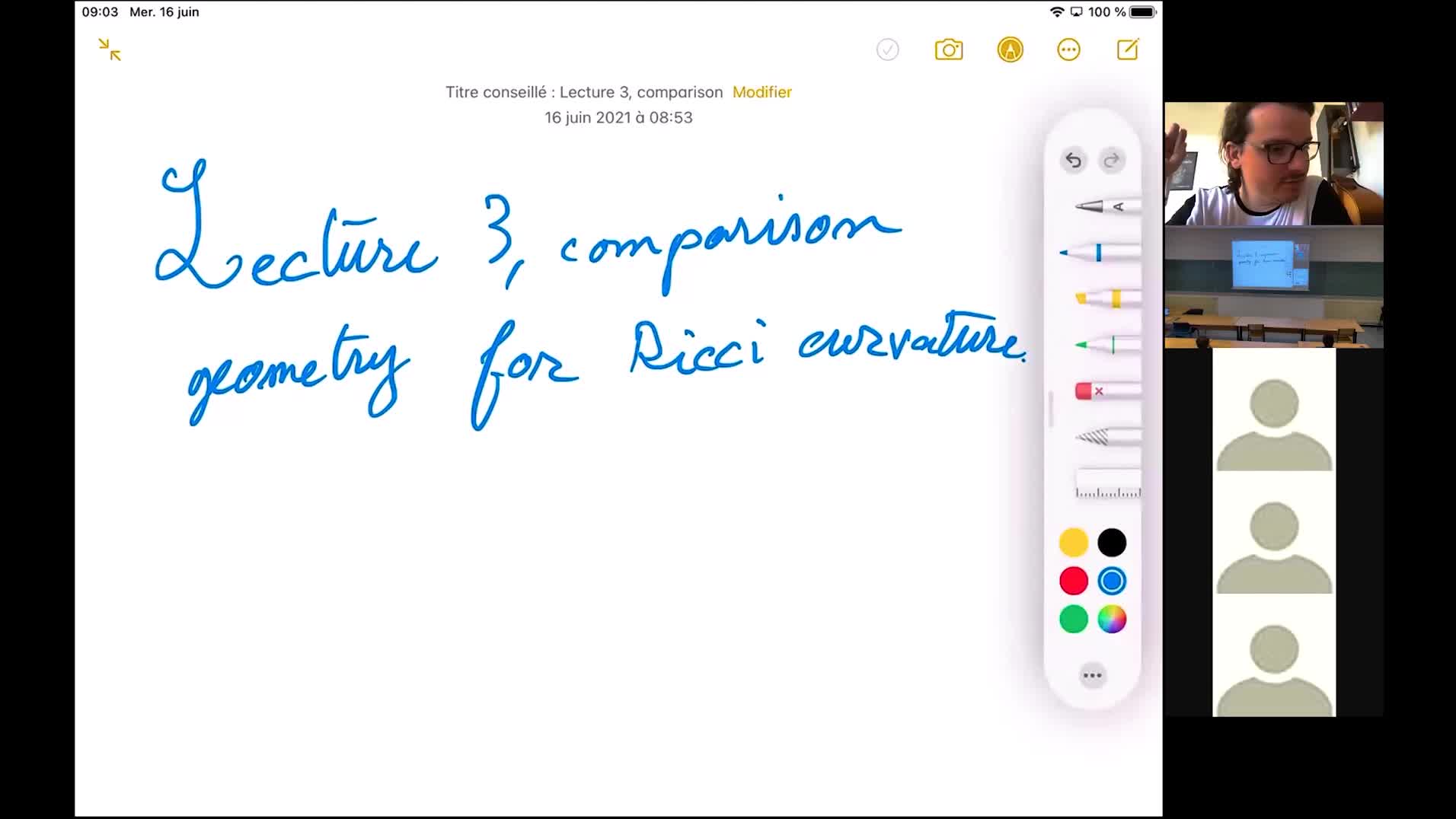
T. Richard - Advanced basics of Riemannian geometry 3
We will present some of the tools used by the more advanced lectures. The topics discussed will include : Gromov Hausdorff distance, comparison theorems for sectional and Ricci curvature, the
Thomas Richard - Lower bounds on Ricci curvature, with a glimpse on limit spaces (Part 4)
The goal of these lectures is to introduce some fundamental tools in the study of manifolds with a lower bound on Ricci curvature. We will first state and prove the laplacian comparison theorem
Thomas Richard - Lower bounds on Ricci curvature, with a glimpse on limit spaces (Part 1)
The goal of these lectures is to introduce some fundamental tools in the study of manifolds with a lower bound on Ricci curvature. We will first state and prove the laplacian comparison theorem