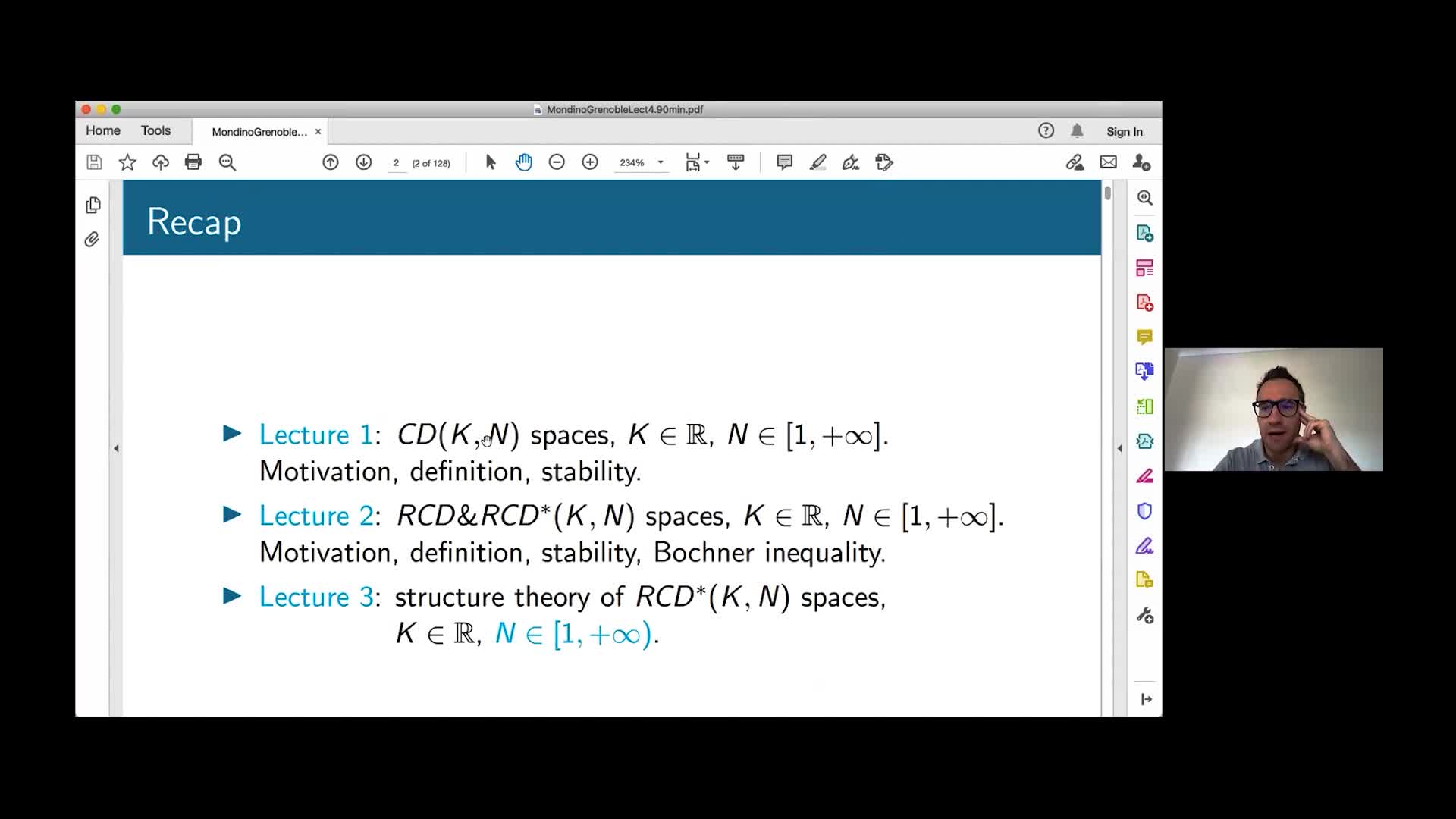
A. Mondino - Metric measure spaces satisfying Ricci curvature lower bounds 4
The idea of compactifying the space of Riemannian manifolds satisfying Ricci curvature lower bounds goes back to Gromov in the '80ies and was pushed by Cheeger-Colding in the ‘90ies, who