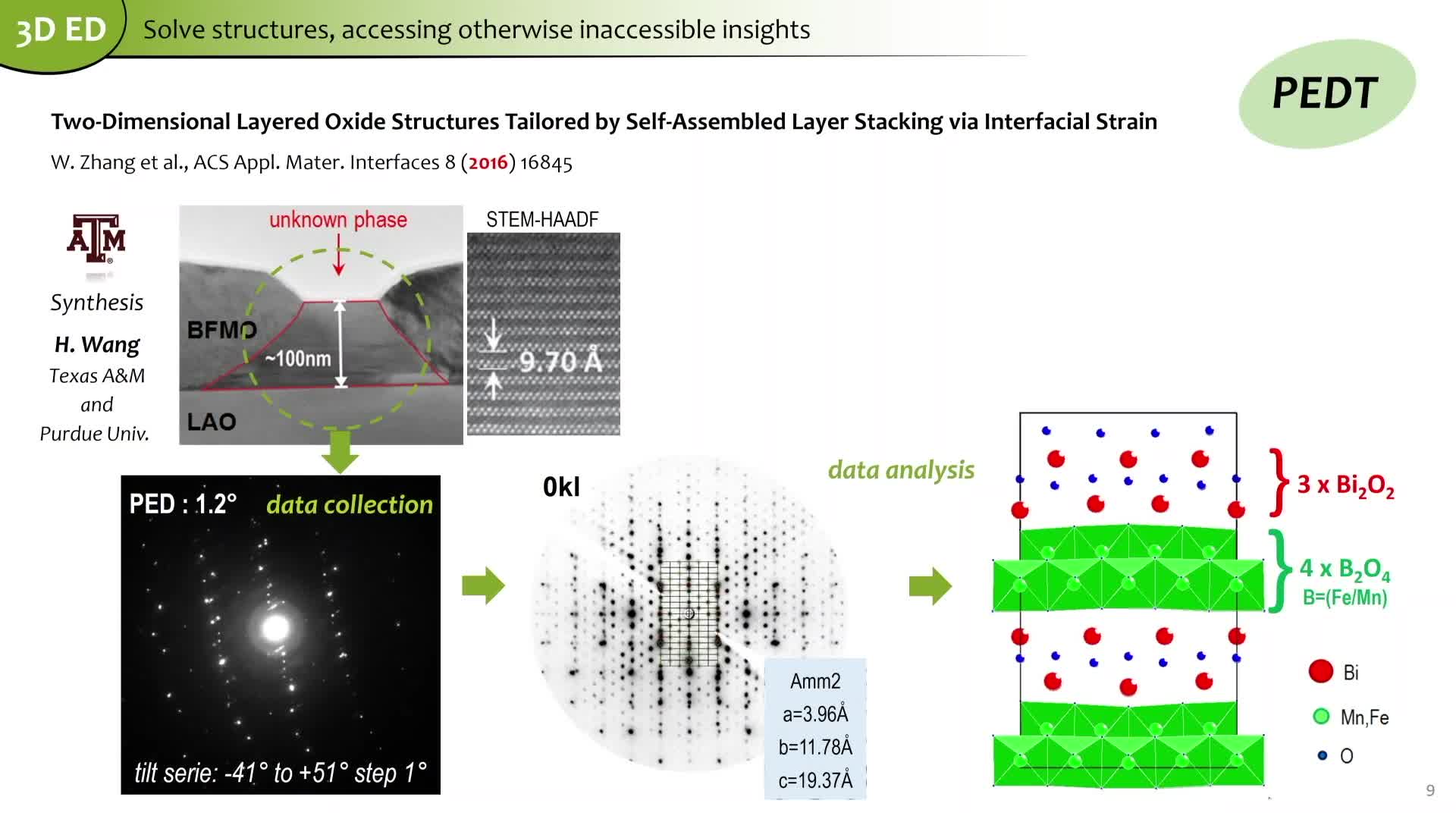
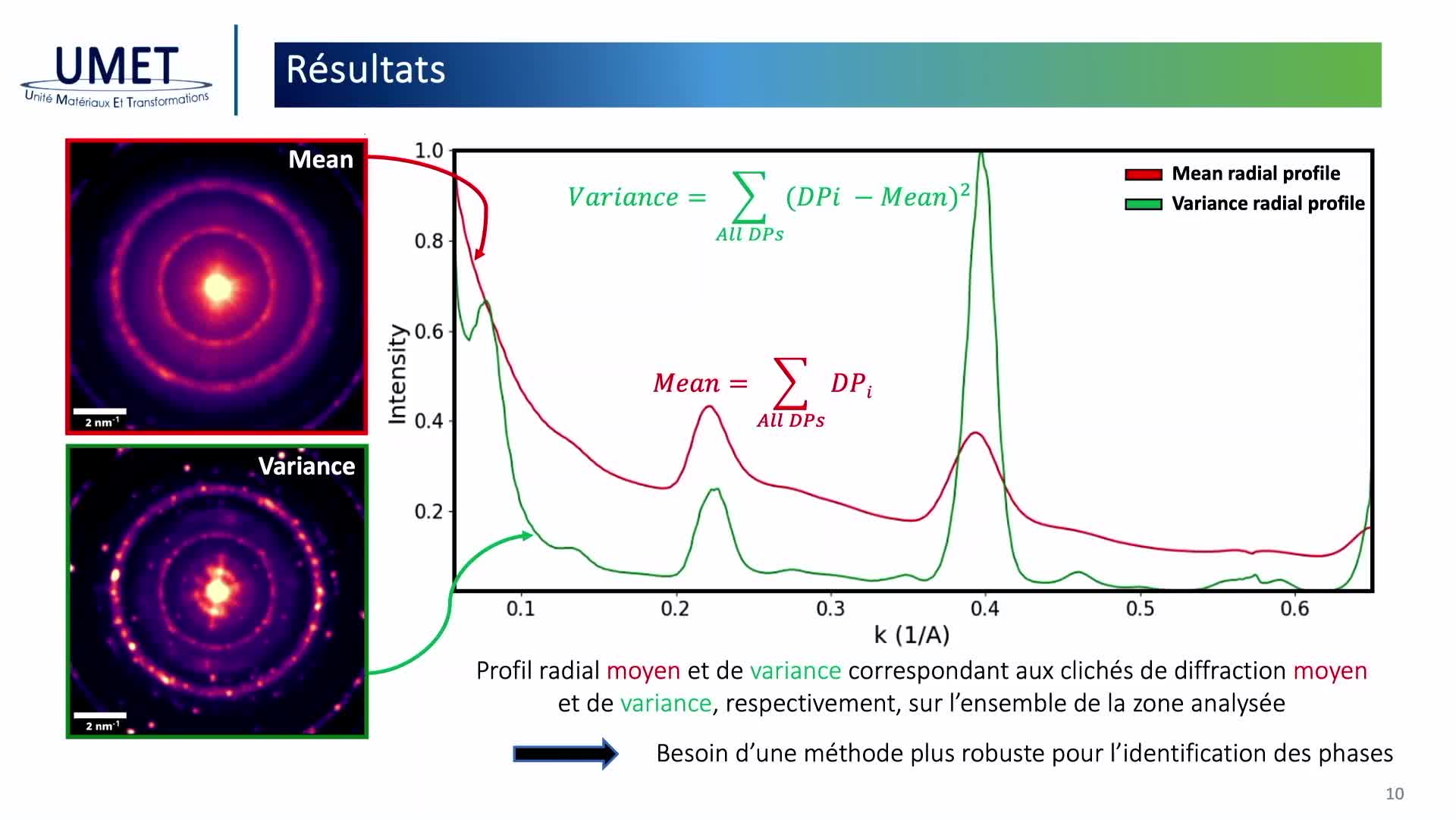
Chapitres
- Présentation01'19"
- Introduction04'42"
- Les structures cristallines04'42"
- La diffraction04'42"
- La quasi-périodicité et les quasi-cristaux04'42"
- Le sens physique de l'espace complémentaire04'42"
- La notion de quasi-symétrie03'27"
- Conclusion03'36"
- Questions: partie 104'42"
- Questions: partie 240'21"
Notice
Les cristaux et les quasi-cristaux
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
"Un ""cristal"" est un solide dont les atomes se répartissent de façon triplement périodique dans l'espace. A cette définition, datant du début du siècle, l'Union Internationale de Cristallographie (IUCr) a ajouté en 1991, celle de ""cristal apériodique"", solide sans périodicité tri-dimensionnelle mais présentant un spectre de diffraction essentiellement discret. Ce sont les phases incommensurables, dont le premier exemple fut découvert en 1936 par Jonhson et Linde, et les quasicristaux découverts en 1982 par Dany Scechtman. Ces nouveaux venus ont bouleversé le paysage de la cristallographie conduisant à la quasicristallographie. La cristallographie s'appuie sur la notion de symétrie c'est-à-dire d'invariance. Celle-ci se rencontre en physique dans de multiples contextes. De la simple invariance géométrique de superposition d'un objet sur lui-même à la définition des grandeurs premières d'un système mécanique ou celle de la forme d'une équation d'état, la symétrie est la traduction rationnelle des redondances de la nature qui en permet une description minimale, nécessaire nulle part mais utile partout. La cristallographie utilise l'expression la plus élémentaire de la symétrie, celle immédiatement visuelle de la géométrie dont les éléments sont les isométries de l'espace euclidien, l'inversion, la rotation, la réflexion dans un miroir, auxquelles s'ajoute, un cristal idéal étant supposé infini, la translation dans l'espace. Déplacer le cristal d'un nombre entier de fois l'une quelconque de ses périodes revient à le superposer exactement ; c'est une opération d'invariance. "
Intervention / Responsable scientifique
Thème
Documentation
Documents pédagogiques
Texte disponble en téléchargement
Dans la même collection
-
Les matériaux magnétiques : de la boussole à l'électronique de spin
PiecuchMichelLe mot magnétisme reste chargé de mystères, pourtant les phénomènes magnétiques sont connus depuis trois mille ans et les matériaux magnétiques sont omniprésents dans notre environnement. Le but de
-
L'utilisation des rayons X pour l'analyse de la matière
PetroffYvesLe rayonnement synchrotron est devenu en quelques années la principale source de rayons X. Il est émis par des particules chargées (électrons) qui sont accélérées par des champs magnétiques dans des
-
L'univers étrange du froid : à la limite du zéro absolu
GodfrinHenriAu voisinage du zéro absolu de température, la matière se transforme, adoptant des comportements que notre intuition a de la peine à appréhender. Certains gaz liquéfiés deviennent superfluides, s
-
Microscopies en champ proche
RoditchevDimitriL'homme a toujours cherché à observer le monde de l'infiniment petit qui l'entoure, le monde invisible à l'oeil nu. Pour cela, il invente la loupe (XVe siècle), puis le microscope optique (XVIIe
-
Conductivité et supraconductivité
LewinerJacquesLa matière est constituée d'atomes qui présentent beaucoup de points communs : un noyau, autour duquel des électrons gravitent. Dans ces conditions, pourquoi certains matériaux sont-ils isolants et
-
Comment les révolutions de l'information et des communications ont-elles été possibles ?
WeisbuchClaudeLes révolutions de l'information et des communications vont continuer à bouleverser tous les domaines de l'activité humaine. Ces révolutions sont nées du codage de l'information sous forme de paquets
-
Physique des tas de sable et de la matière molle
GuyonÉtienne"Matière molle ou douce, objet fragiles, autant d'appellations diverses d'une science au quotidien qui associe des compétences variées de chercheurs. Par exemple, derrière les exemples à goûter de
-
La superfluidité
BalibarSébastien"Peut-on voir au moins une propriété quantique de la matière à l'oeil nu ? Oui, il suffit de regarder de l'hélium liquide à suffisamment basse température. Je montrerai un liquide qui cesse de
-
Fluides et tourbillons
LesieurMarcel"Les récents ouragans sur la France nous ont brutalement rappelé l'importance des fluides tels que l'air et l'eau. Ces fluides obéissent aux lois de la mécanique classique de Newton. Ils sont très
-
Pourquoi la matière change-t-elle d'état : la compétition entre ordre et désordre
BrézinÉdouard"Les changements d'état de la matière, sous l'effet d'une élévation ou d'un abaissement de température, sont des phénomènes bien familiers. De même, on connaît depuis longtemps des substances dont la
Sur le même thème
-
An introduction to small angle x-ray scattering
Impéror-ClercMarianneAn introduction to small angle x-ray scattering
-
-
-
EELS, principe et application à l’étude des nanomatériaux inorganiques
NelayahJaysenEELS, principe et application à l’étude des nanomatériaux inorganiques
-
-
Nanoscale structural heterogeneity of crystalline carbohydrates
OgawaYuNanoscale structural heterogeneity of crystalline carbohydrates
-
-
-
Complémentarité diffraction électronique - diffraction des rayons X appliqués aux protéines
HoussetDominiqueComplémentarité diffraction électronique - diffraction des rayons X appliqués aux protéines
-
-
Analyse structurale par 4D-STEM d’échantillons astéroidaux
JacobDamienAnalyse structurale par 4D-STEM d’échantillons astéroidaux
-
Correction brasse dissymétrique : pratique
CholletDidierLa procédure de remédiation est illustrée par une vidéo d’une séance qui a permis à 2 nageurs de corriger leur brasse.