Notice
KEZAKO : Qu'est-ce qu'une fractale ?
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
Kezako est la série documentaire qui répond à des questions de science. Cet épisode s'interesse aux fractales, cette forme mathématique si particulière que l'on retrouve dans la nature. On aborde aussi le flocon de Koch et sa dimension non entière.
Intervention
Thème
Avec les mêmes intervenants et intervenantes
-
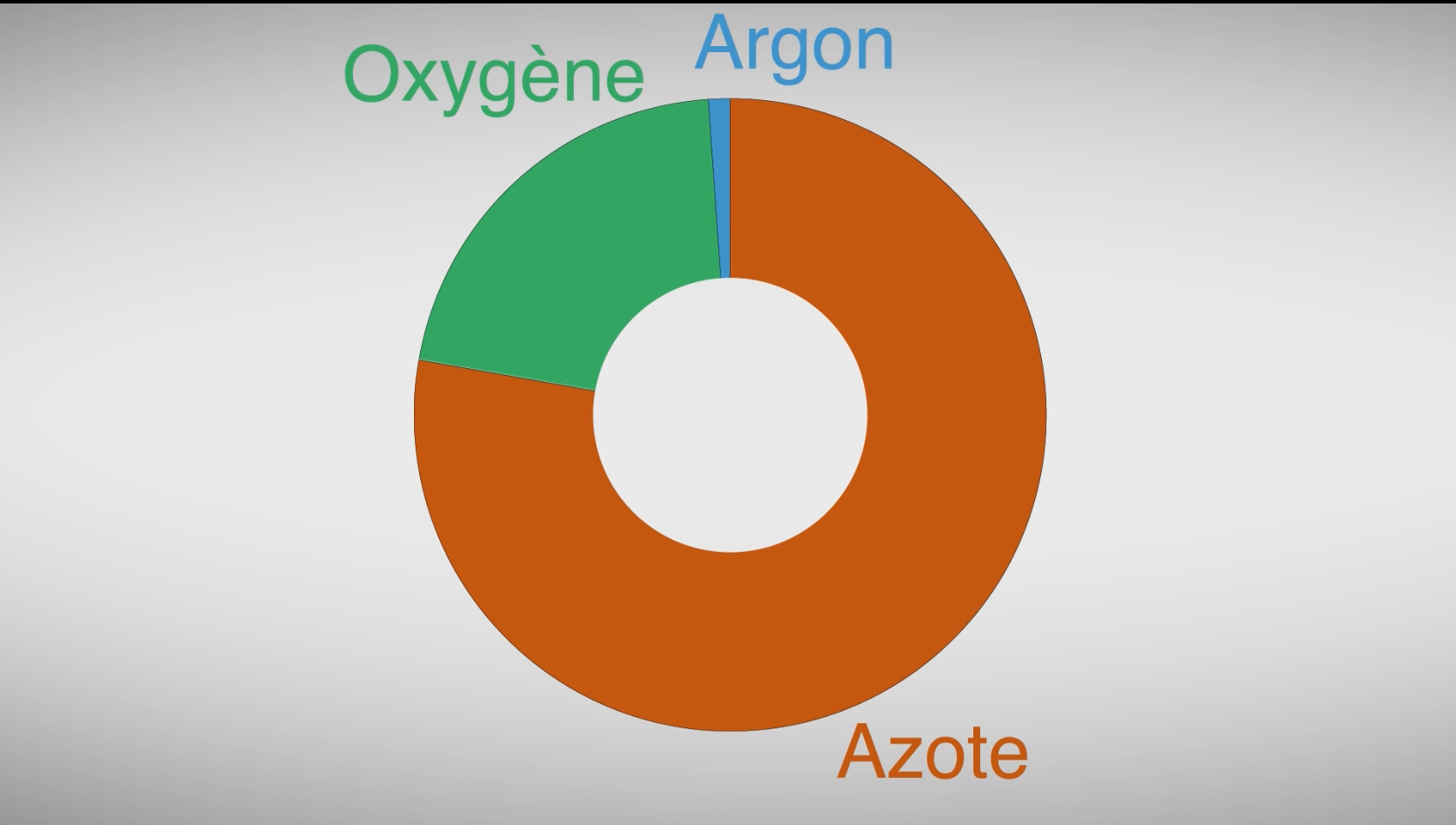
Quelle est la composition de l’air ?
HennequinDanielKezako, la série documentaire qui répond à vos questions de science, aborde cette fois-ci la question "Quelle est la composition de l’air ? ". N'hesitez pas à réagir ou à oser vos questions qui seront
-
Comment sortir des sables mouvants ?
HennequinDanielKezako, la série documentaire qui répond à vos questions de science, aborde cette fois-ci la question "Comment sortir des sables mouvants ? ". N'hesitez pas à réagir ou à oser vos questions qui seront
-
Comment se forment les aurores boréales ?
HennequinDanielKezako, la série documentaire qui répond à vos questions de science, aborde cette fois-ci la question "Comment se forment les aurores boréales ? ". N'hesitez pas à réagir ou à oser vos questions qui
-
Qu'est-ce qu'un mirage ?
HennequinDanielKezako, la série documentaire qui répond à vos questions de science, aborde cette fois-ci la question "Qu'est-ce qu'un mirage ?".N'hesitez pas à réagir ou à oser vos questions qui seront peut être
-
Comment coupe-t-on ?
BeaugeoisMaximeDeltombeDamienKezako, la série documentaire qui répond à vos questions de science, aborde cette fois-ci la question "Comment coupe-t-on ?".N'hesitez pas à réagir ou à oser vos questions qui seront peut être
-
KEZAKO : Comment prédit-on la météo ?
BeaugeoisMaximeHennequinDanielDeltombeDamienKezako est la série qui répond aux questions de science que vous vous posez. Cet épisode traite de la question "Comment prédit-on la météo ?". Il aborde les notions de dépression, d'anticyclone, les
-
KEZAKO : Comment fait-on pour voir en relief ?
BeaugeoisMaximeHennequinDanielDeltombeDamienKezako est la série documentaire qui répond aux questions de science que tout le monde se pose. Cet épisode traite de la question "Comment fait-on pour voir en relief ?". Il traite du mécanisme de
-
KEZAKO : D'où part l'éclair : du ciel ou du sol ?
BeaugeoisMaximeHennequinDanielDeltombeDamienKezako, la série documentaire qui répond à vos questions de science, aborde cette fois-ci la question "D'où part l'éclair : du ciel ou du sol ?" N'hesitez pas à réagir ou à poser vos questions qui
-
KEZAKO : Comment a-t-on découvert le nombre Pi ?
BeaugeoisMaximeDeltombeDamienHennequinDanielKezako est la série documentaire qui répond à vos questions de sciences. Cet épisode s'interesse à un nombre bien connu de tous mais portant tout autant de mystère, le nombre Pi. Retour sur sa
-
KEZAKO : Quel effet le vent a-t-il sur la sensation de chaleur ?
BeaugeoisMaximeHennequinDanielDeltombeDamienKezako, la série documentaire qui répond à vos questions de science, aborde cette fois-ci la question "Quel effet le vent a-t-il sur la sensation de chaleur ?" ou "Pourquoi a-t-on plus froid quand il
-
KEZAKO : Comment fonctionne une échographie ?
BeaugeoisMaximeHennequinDanielDeltombeDamienKezako est la série documentaire qui répond aux questions de science que tout le monde se pose. Cet épisode traite de la question "Comment fonctionne une échographie ?". Il détaille le principe des
-
KEZAKO : De quoi est composée la matière ? Pourquoi est-ce solide, liquide ou gazeux ?
BeaugeoisMaximeHennequinDanielDeltombeDamienKezako est la série qui répond à vos questions de science. Cet épisode traite de deux questions : "De quoi est composée la matière ? Pourquoi est-ce solide, liquide ou gazeux ?". Il aborde les notions
Sur le même thème
-
Aurel PAGE - Cohomology of arithmetic groups and number theory: geometric, asymptotic and computati…
PageAurel regisIn this lecture series, the first part will be dedicated to cohomology of arithmetic groups of lower ranks (e.g., Bianchi groups), their associated geometric models (mainly from hyperbolic geometry)
-
Phong NGUYEN - Recent progress on lattices's computations 2
NguyenPhong Q.This is an introduction to the mysterious world of lattice algorithms, which have found many applications in computer science, notably in cryptography. We will explain how lattices are represented by
-
Oussama Hamza - Hilbert series and mild groups
Let $p$ be an odd prime number and $G$ a finitely generated pro-$p$ group. Define $I(G)$ the augmentation ideal of the group algebra of $G$ over $F_p$ and define the Hilbert series of $G$ by: $G(t):
-
Gabriele NEBE - Lattices, Perfects lattices, Voronoi reduction theory, modular forms, computations …
NebeGabrieleThe talks of Coulangeon will introduce the notion of perfect, eutactic and extreme lattices and the Voronoi's algorithm to enumerate perfect lattices (both Eulcidean and Hermitian). The talk of Nebe
-
Alexander HULPKE - Computational group theory, cohomology of groups and topological methods 4
The lecture series will give an introduction to the computer algebra system GAP, focussing on calculations involving cohomology. We will describe the mathematics underlying the algorithms, and how to
-
Alexander HULPKE - Computational group theory, cohomology of groups and topological methods 5
The lecture series will give an introduction to the computer algebra system GAP, focussing on calculations involving cohomology. We will describe the mathematics underlying the algorithms, and how to
-
Zachary Himes - On not the rational dualizing module for $\text{Aut}(F_n)$
Bestvina--Feighn proved that $\text{Aut}(F_n)$ is a rational duality group, i.e. there is a $\mathbb{Q}[\text{Aut}(F_n)]$-module, called the rational dualizing module, and a form of Poincar\'e duality
-
Tobias Moede - Coclass theory for nilpotent associative algebras
The coclass of a finite p-group of order p^n and class c is defined as n-c. Using coclass as the primary invariant in the investigation of finite p-groups turned out to be a very fruitful approach.
-
Alexandre Booms : « Usage de matériel pédagogique adapté en géométrie : une transposition à interro…
« Usage de matériel pédagogique adapté en géométrie : une transposition à interroger ». Alexandre Booms, doctorant (Université de Reims Champagne-Ardenne - Cérep UR 4692)
-
Paul GUNNELLS - Cohomology of arithmetic groups and number theory: geometric, asymptotic and comput…
GunnellsPaul E.In this lecture series, the first part will be dedicated to cohomology of arithmetic groups of lower ranks (e.g., Bianchi groups), their associated geometric models (mainly from hyperbolic geometry)
-
Paul GUNNELLS - Cohomology of arithmetic groups and number theory: geometric, asymptotic and comput…
GunnellsPaul E.In this lecture series, the first part will be dedicated to cohomology of arithmetic groups of lower ranks (e.g., Bianchi groups), their associated geometric models (mainly from hyperbolic geometry)
-
Paul GUNNELLS - Cohomology of arithmetic groups and number theory: geometric, asymptotic and comput…
GunnellsPaul E.In this lecture series, the first part will be dedicated to cohomology of arithmetic groups of lower ranks (e.g., Bianchi groups), their associated geometric models (mainly from hyperbolic geometry)
