Rencontres du GDR AFHP 2019
Conférences
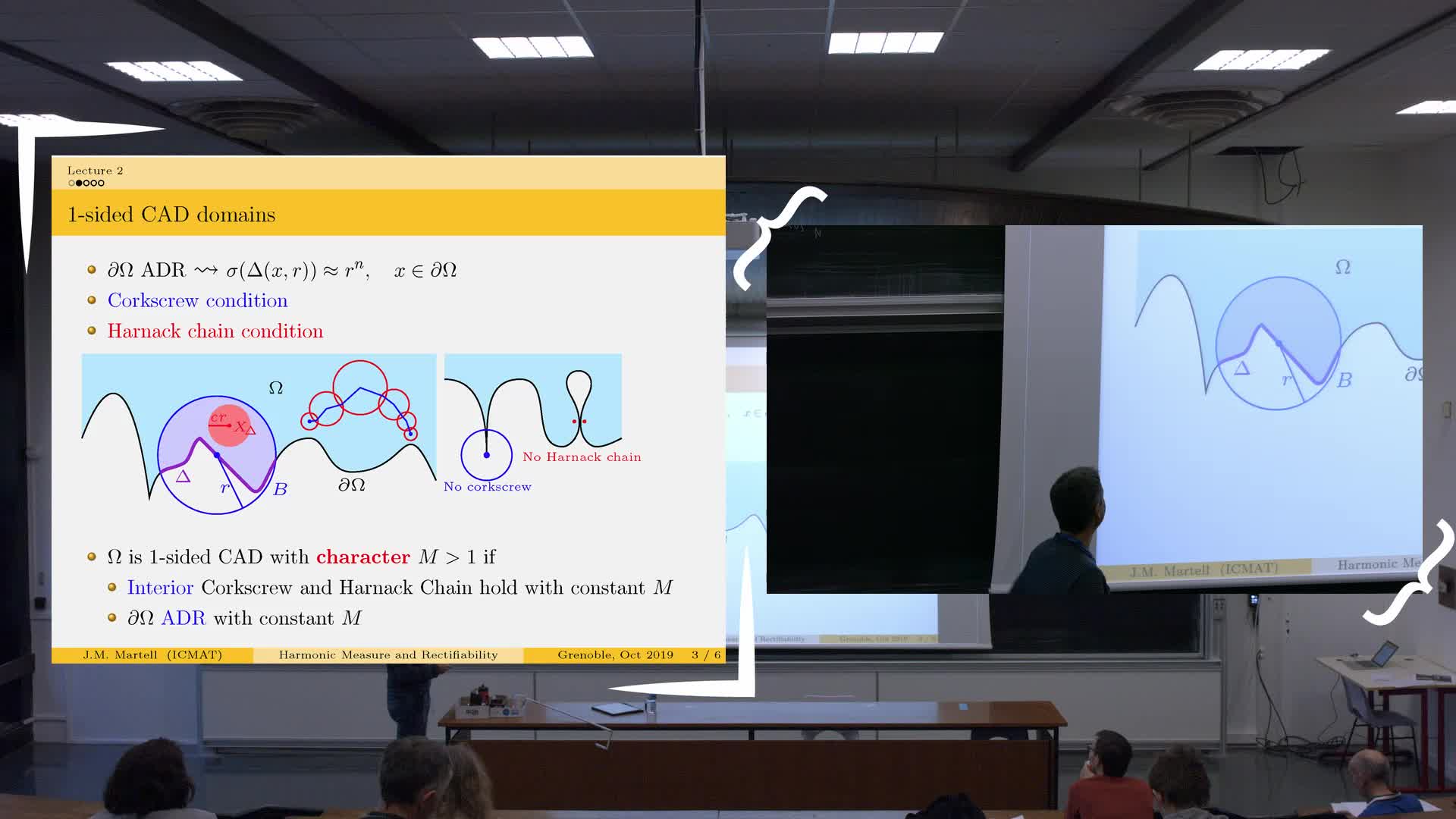
J.-M. Martell - A minicourse on Harmonic measure and Rectifiability (Part 3)
Solving the Dirichlet boundary value problem for an elliptic operator amounts to study the good properties of the associated elliptic measure. In the context of domains having an Ahlfors regular
J.-M. Martell - A minicourse on Harmonic measure and Rectifiability (Part 2)
Solving the Dirichlet boundary value problem for an elliptic operator amounts to study the good properties of the associated elliptic measure. In the context of domains having an Ahlfors regular
J.-M. Martell - A minicourse on Harmonic measure and Rectifiability (Part 1)
Solving the Dirichlet boundary value problem for an elliptic operator amounts to study the good properties of the associated elliptic measure. In the context of domains having an Ahlfors regular
I. Gentil - Le problème de Schrödinger, un point de vue analytique (Part 2)
Ce cours est divisé en trois parties, le but étant de comprendre le problème de Schrödinger avec un point de vue analytique. Le premier cours porte sur le problème de Schrödinger. C’est un
I. Gentil - Le problème de Schrödinger, un point de vue analytique (Part 1)
Ce cours est divisé en trois parties, le but étant de comprendre le problème de Schrödinger avec un point de vue analytique. Le premier cours porte sur le problème de Schrödinger. C’est un
I. Gentil - Le problème de Schrödinger, un point de vue analytique (Part 3)
Ce cours est divisé en trois parties, le but étant de comprendre le problème de Schrödinger avec un point de vue analytique. Le premier cours porte sur le problème de Schrödinger. C’est un
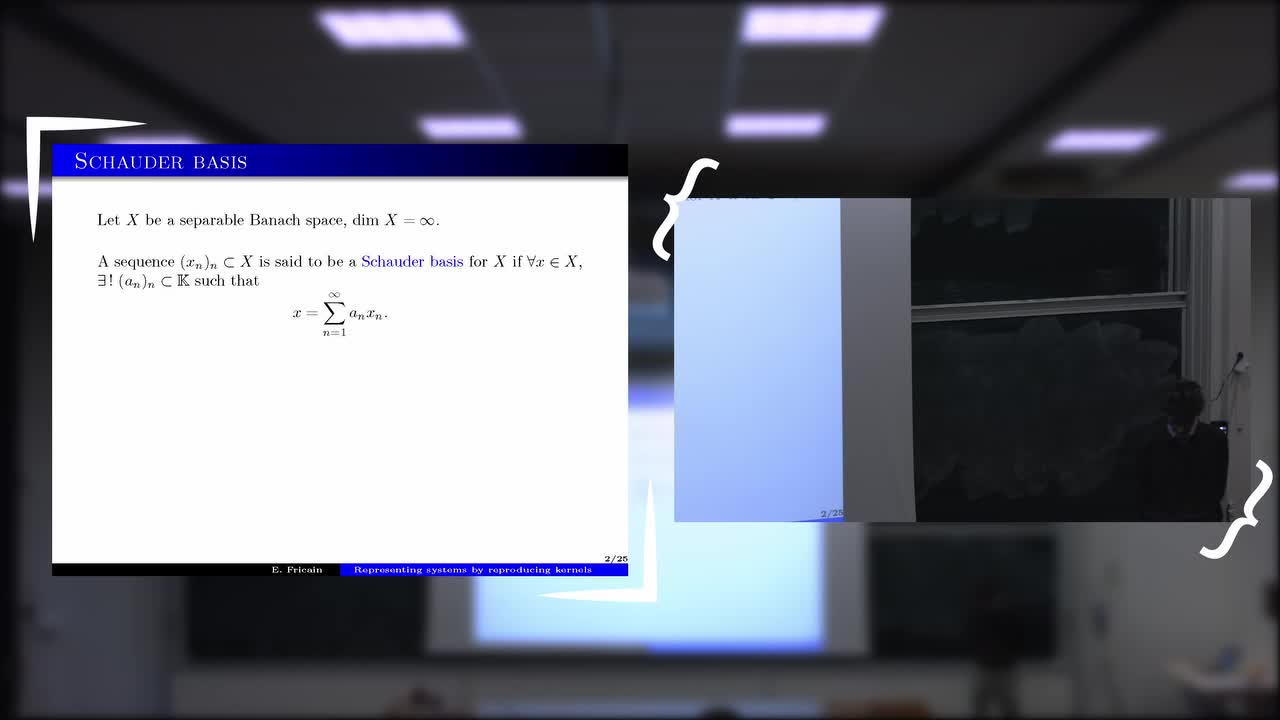
E. Fricain - Systèmes représentant dans les espaces de Hilbert de fonctions analytiques
Dans les espaces de Banach de dimension infinie, la notion de base de Schauder est classique et bien étudi ée. Elle permet de représenter tout élément de l’espace comme une série des
I. Chalendar - Sur les pas de Gabriel Koenigs
Sur les pas de Gabriel Koenigs : spectre des opérateurs de composition sur l’espace de Fréchet des fonctions holomorphes sur le disque unité Étant donnée une application holomorphe f du disque unité
Intervenants
Instituto de Ciencias Matemáticas, Madrid (2011)
Titulaire d'un doctorat d'université en mathématiques : probabilités (Toulouse 3, 2001)
Mathématicien. Maître de conférence à l'Université Paris-Dauphine et membre du laboratoire CEREMADE, UMR CNRS 7534 (en 2002). Professeur à l'université Claude Bernard Lyon 1 et membre de l'Institut Camille Jordan (en 2014)
Titulaire d'un doctorat en Mathématiques pures (Bordeaux 1, 1996)
Enseignante-chercheuse au sein de l'Université Gustave Eiffel, membre de l'équipe "Analyse en grande dimension" du Laboratoire d'Analyse et Mathématiques Appliquées (LAMA - UMR CNRS 8050)
Titulaire d'un docotrat en Mathématiques Pures (Bordeaux 1, 1999)
Titulaire d'une Habilitation des Recherches en Mathématiques (Lyon 1, 2008)
Enseignant-chercheur au sein du département Mathématiques de la Faculté des Sciences et Technologies de l'Université de Lille, responsable de l'équipe "Analyse" du laboratoire Paul Painlevé (UMR CNRS 8524)