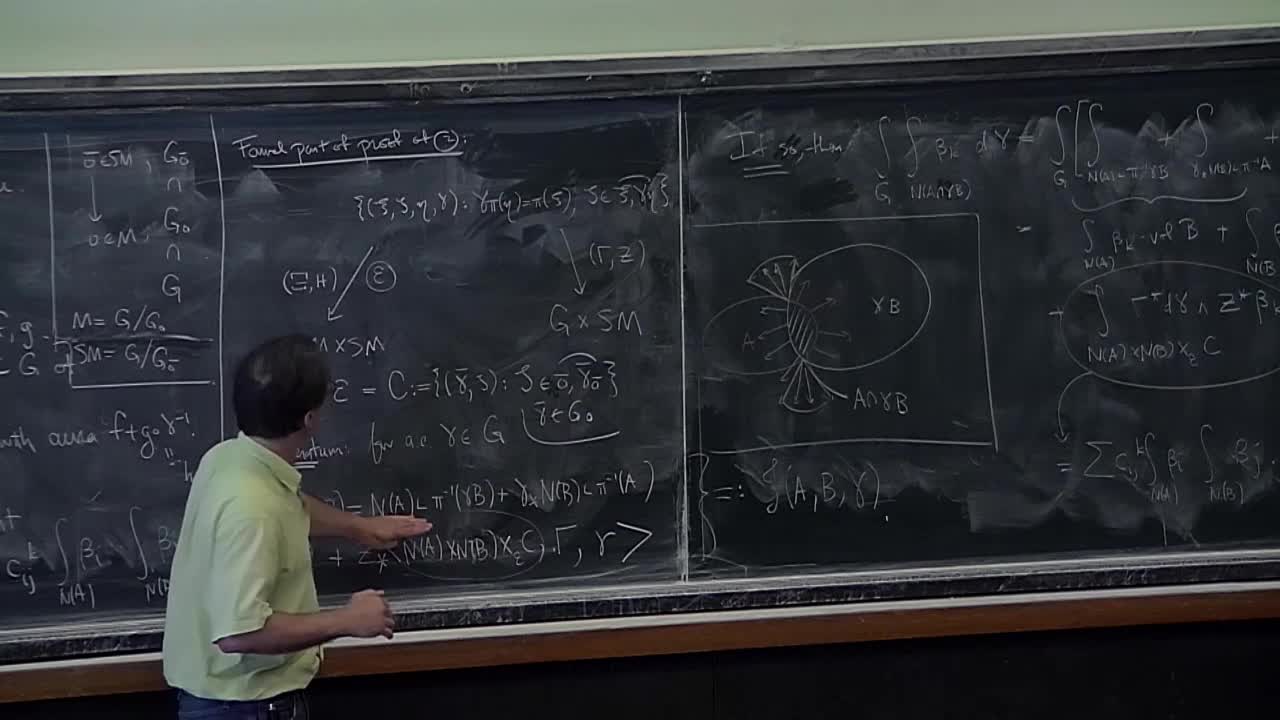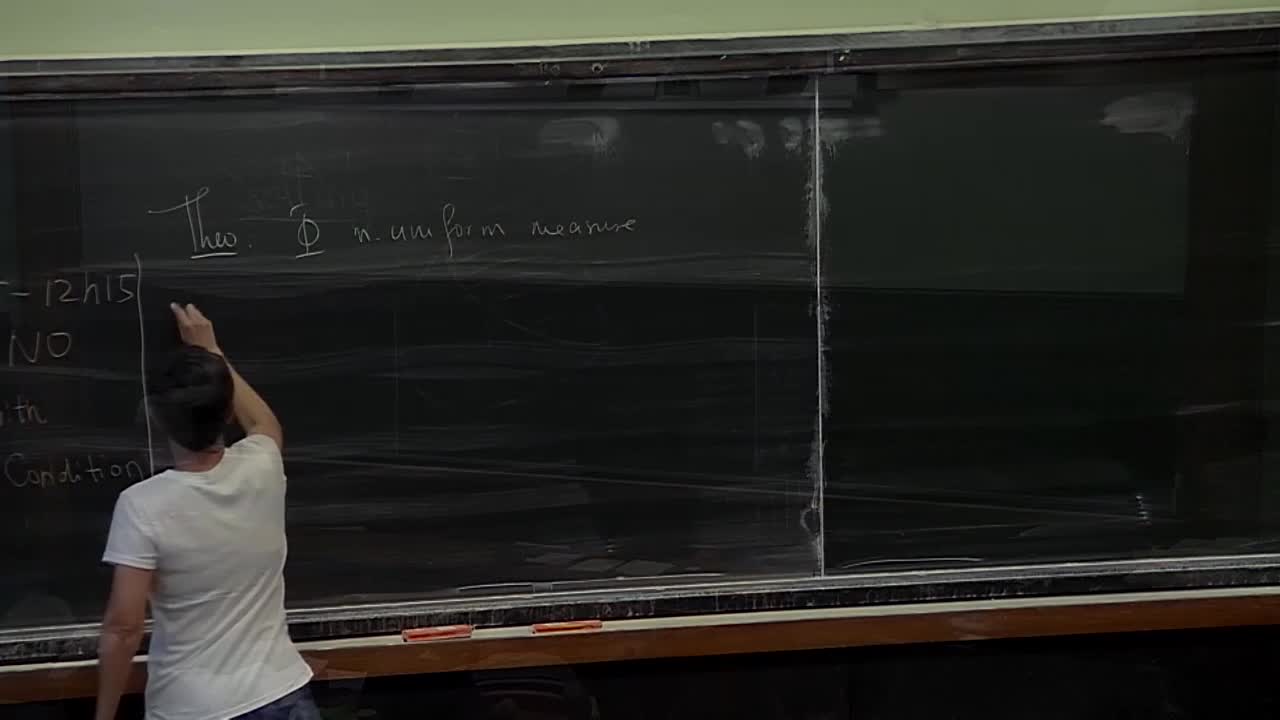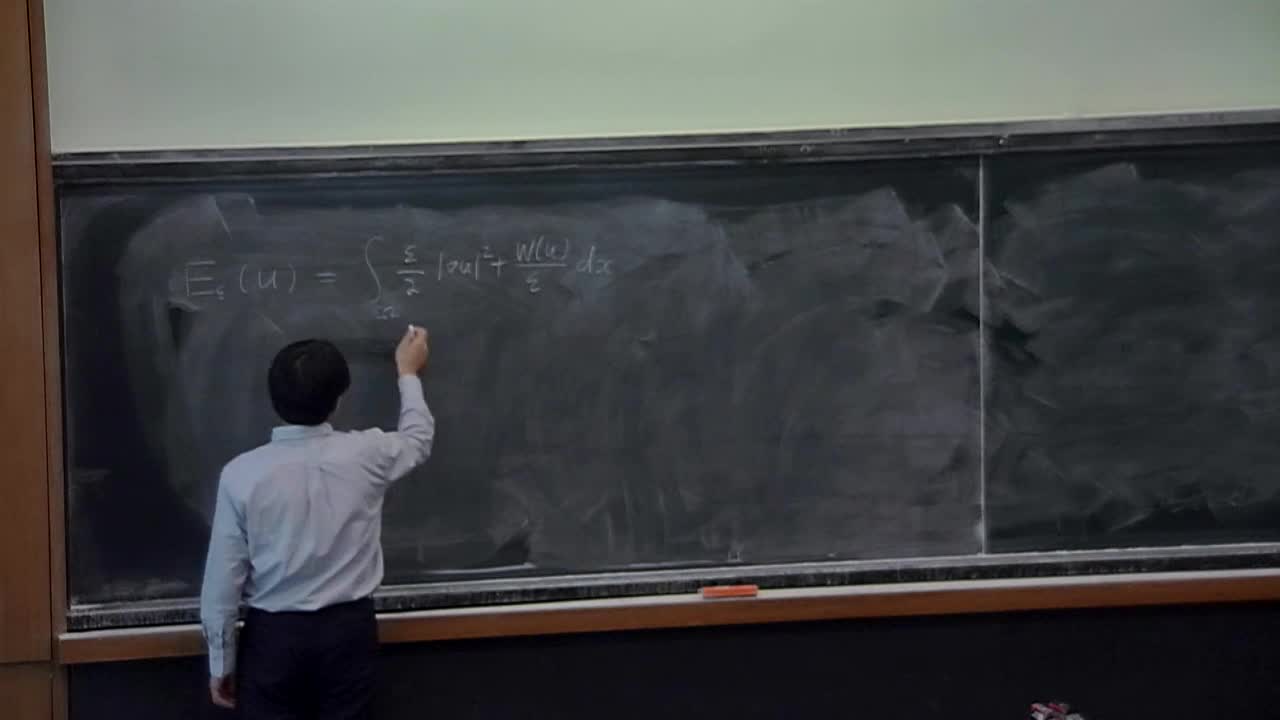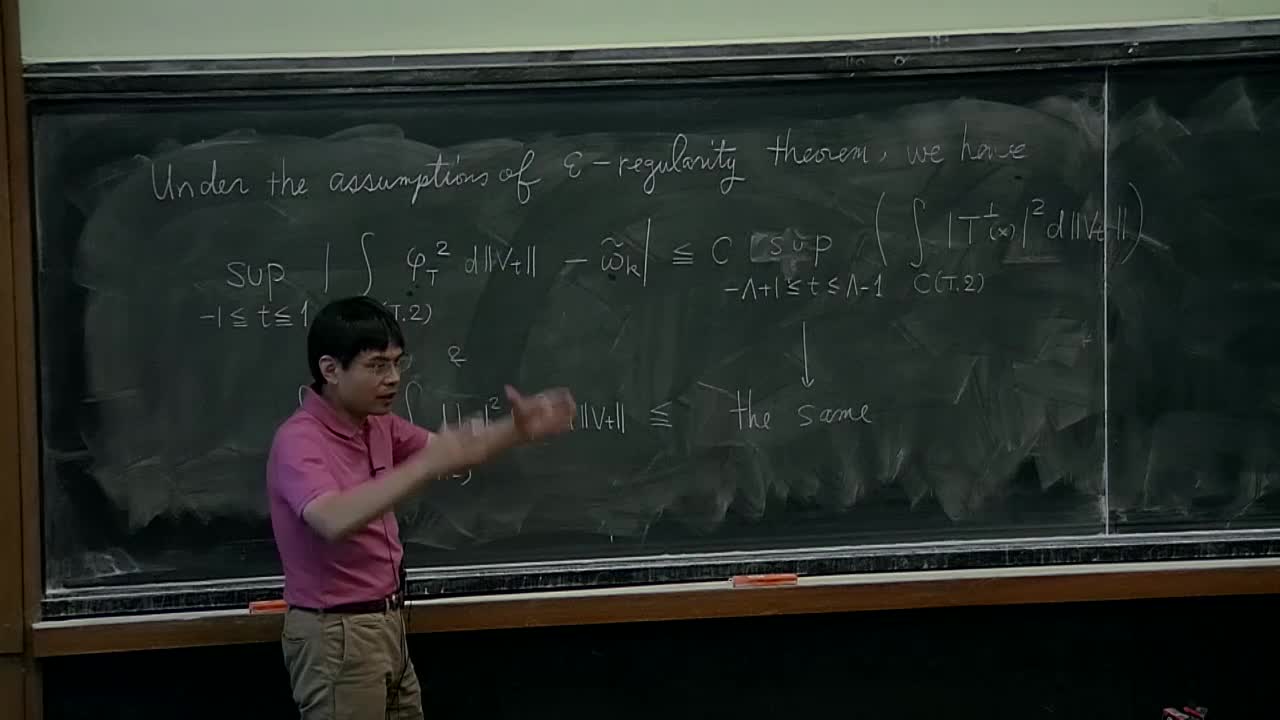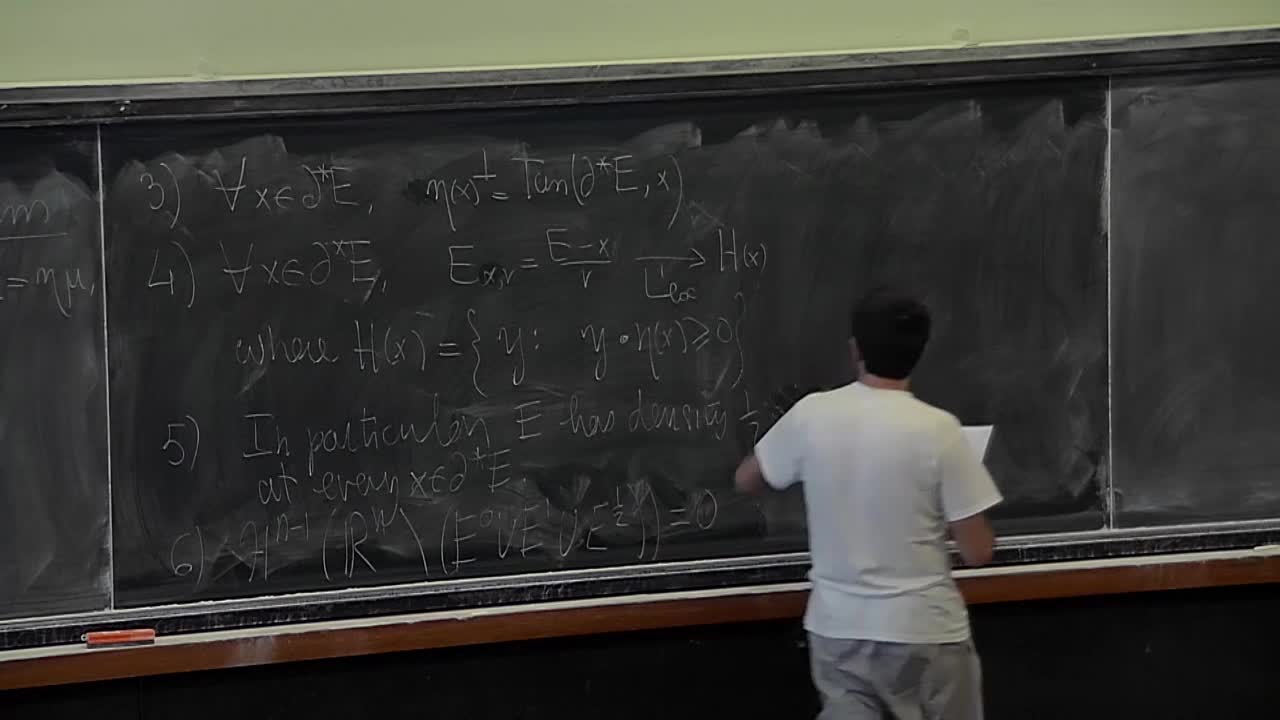2015

Vidéos
Matthias Röger - A curvature energy for bilayer membranes
A curvature energy for bilayer membranes
Giovanni Pisante - Duality approach to a variational problem involving a polyconvex integrand
Duality approach to a variational problem involving a polyconvex integrand
Neshan Wickramasereka - Stability in minimal and CMC hypersurfaces
indisponible
Gian Paolo Leonardi - Towards a unified theory of surface discretization
indisponible
Free discontinuity problems and Robin boundary conditions
par Alessandro Giacomini, université de Brescia
Camillo De Lellis - Center manifolds and regularity of area-minimizing currents (Part 2)
A celebrated theorem of Almgren shows that every integer rectifiable current which minimizes (locally) the area is a smooth submanifold except for a singular set of codimension at most 2.
Camillo De Lellis - Center manifolds and regularity of area-minimizing currents (Part 1)
A celebrated theorem of Almgren shows that every integer rectifiable current which minimizes (locally) the area is a smooth submanifold except for a singular set of codimension at most 2.
Joseph Fu - Integral geometric regularity (Part 5)
In the original form given by Blaschke in the 1930s, the famous Principal Kinematic Formula expresses the Euler characteristic of the intersection of two sufficiently regular objects in
Joseph Fu - Integral geometric regularity (Part 4)
In the original form given by Blaschke in the 1930s, the famous Principal Kinematic Formula expresses the Euler characteristic of the intersection of two sufficiently regular objects in
Joseph Fu - Integral geometric regularity (Part 3)
In the original form given by Blaschke in the 1930s, the famous Principal Kinematic Formula expresses the Euler characteristic of the intersection of two sufficiently regular objects in
Joseph Fu - Integral geometric regularity (Part 2)
In the original form given by Blaschke in the 1930s, the famous Principal Kinematic Formula expresses the Euler characteristic of the intersection of two sufficiently regular objects in
Tatiana Toro - Geometry of measures and applications (Part 5)
In the 1920's Besicovitch studied linearly measurable sets in the plane, that is sets with locally finite "length". The basic question he addressed was whether the infinitesimal properties of
Tatiana Toro - Geometry of measures and applications (Part 4)
In the 1920's Besicovitch studied linearly measurable sets in the plane, that is sets with locally finite "length". The basic question he addressed was whether the infinitesimal properties of
Tatiana Toro - Geometry of measures and applications (Part 3)
In the 1920's Besicovitch studied linearly measurable sets in the plane, that is sets with locally finite "length". The basic question he addressed was whether the infinitesimal properties of
Tatiana Toro - Geometry of measures and applications (Part 2)
In the 1920's Besicovitch studied linearly measurable sets in the plane, that is sets with locally finite "length". The basic question he addressed was whether the infinitesimal properties of
Tatiana Toro - Geometry of measures and applications (Part 1)
In the 1920's Besicovitch studied linearly measurable sets in the plane, that is sets with locally finite "length". The basic question he addressed was whether the infinitesimal properties of
Yoshihiro Tonegawa - Analysis on the mean curvature flow and the reaction-diffusion approximation (…
The course covers two separate but closely related topics. The first topic is the mean curvature flow in the framework of GMT due to Brakke. It is a flow of varifold moving by the generalized
Yoshihiro Tonegawa - Analysis on the mean curvature flow and the reaction-diffusion approximation (…
The course covers two separate but closely related topics. The first topic is the mean curvature flow in the framework of GMT due to Brakke. It is a flow of varifold moving by the generalized
Yoshihiro Tonegawa - Analysis on the mean curvature flow and the reaction-diffusion approximation (…
The course covers two separate but closely related topics. The first topic is the mean curvature flow in the framework of GMT due to Brakke. It is a flow of varifold moving by the generalized
Yoshihiro Tonegawa - Analysis on the mean curvature flow and the reaction-diffusion approximation (…
The course covers two separate but closely related topics. The first topic is the mean curvature flow in the framework of GMT due to Brakke. It is a flow of varifold moving by the generalized
Yoshihiro Tonegawa - Analysis on the mean curvature flow and the reaction-diffusion approximation (…
The course covers two separate but closely related topics. The first topic is the mean curvature flow in the framework of GMT due to Brakke. It is a flow of varifold moving by the generalized
Joseph Fu - Integral geometric regularity (Part 1)
In the original form given by Blaschke in the 1930s, the famous Principal Kinematic Formula expresses the Euler characteristic of the intersection of two sufficiently regular objects in
Camillo De Lellis - Center manifolds and regularity of area-minimizing currents (Part 5)
A celebrated theorem of Almgren shows that every integer rectifiable current which minimizes (locally) the area is a smooth submanifold except for a singular set of codimension at most 2.
Camillo De Lellis - Center manifolds and regularity of area-minimizing currents (Part 4)
A celebrated theorem of Almgren shows that every integer rectifiable current which minimizes (locally) the area is a smooth submanifold except for a singular set of codimension at most 2.
Camillo De Lellis - Center manifolds and regularity of area-minimizing currents (Part 3)
A celebrated theorem of Almgren shows that every integer rectifiable current which minimizes (locally) the area is a smooth submanifold except for a singular set of codimension at most 2.
Giovanni Alberti - Introduction to minimal surfaces and finite perimeter sets (Part 5)
In these lectures I will first recall the basic notions and results that are needed to study minimal surfaces in the smooth setting (above all the area formula and the first variation of the
Giovanni Alberti - Introduction to minimal surfaces and finite perimeter sets (Part 4)
In these lectures I will first recall the basic notions and results that are needed to study minimal surfaces in the smooth setting (above all the area formula and the first variation of the
Giovanni Alberti - Introduction to minimal surfaces and finite perimeter sets (Part 3)
In these lectures I will first recall the basic notions and results that are needed to study minimal surfaces in the smooth setting (above all the area formula and the first variation of the
Giovanni Alberti - Introduction to minimal surfaces and finite perimeter sets (Part 2)
In these lectures I will first recall the basic notions and results that are needed to study minimal surfaces in the smooth setting (above all the area formula and the first variation of the
Giovanni Alberti - Introduction to minimal surfaces and finite perimeter sets (Part 1)
In these lectures I will first recall the basic notions and results that are needed to study minimal surfaces in the smooth setting (above all the area formula and the first variation of the
Intervenants et intervenantes
Professeur de mathématiques à l'Université de Pise (Italie) en 2020
Mathématicien. En poste à la National and Kapodistrian University, Athènes, Grèce (en 2018)
Professeur en analyse mathématique
Mathématicien.- Docteur ès sciences mathématiques (Paris 11, 1986). Professeur de mathématiques, Université de Paris-Sud (Orsay) depuis Septembre 1989 (en 2020)
Professeur, en poste à l'Institut de Mathématiques de l'Université de Zurich, Suisse (en 2008)
Domaine de recherche : EDP, Théorie de Mesure Géométrique
Professeur associée de mathématiques à l'université de Brescia (Italie) (en 2015)
Mathématicien. En poste au Mathematisches Institut de l'Université de Leipzig (2015)
Co-directeur d'une thèse en Mathématiques soutenue à Lyon 1 en 2014
Auteur d'une thèse de : mathématiques, Université Paris-Sud 11, Orsay (en 2010)
Maîtresse de conférences en mathématiques à l'Université Lyon 1 et membre de l'Institut Camille Jordan (depuis 2014-09)
En poste : Universita degli Studi di Firenze, Italie (en 2012)
Professeur au département de mathématiques et de physique de l'Université Vanvitelli de Campanie (2015)
Mathématicien. Professeur à l'Université technique de Dortmund. Membre du groupe de Biomathématiques (2016)
Ph.D. (New York University, 1993)
Mathématicien. En poste : Tokyo Institute of Technology, Japon (en 2019)
Mathématicien. En poste à l'University of Cambridge (2015)