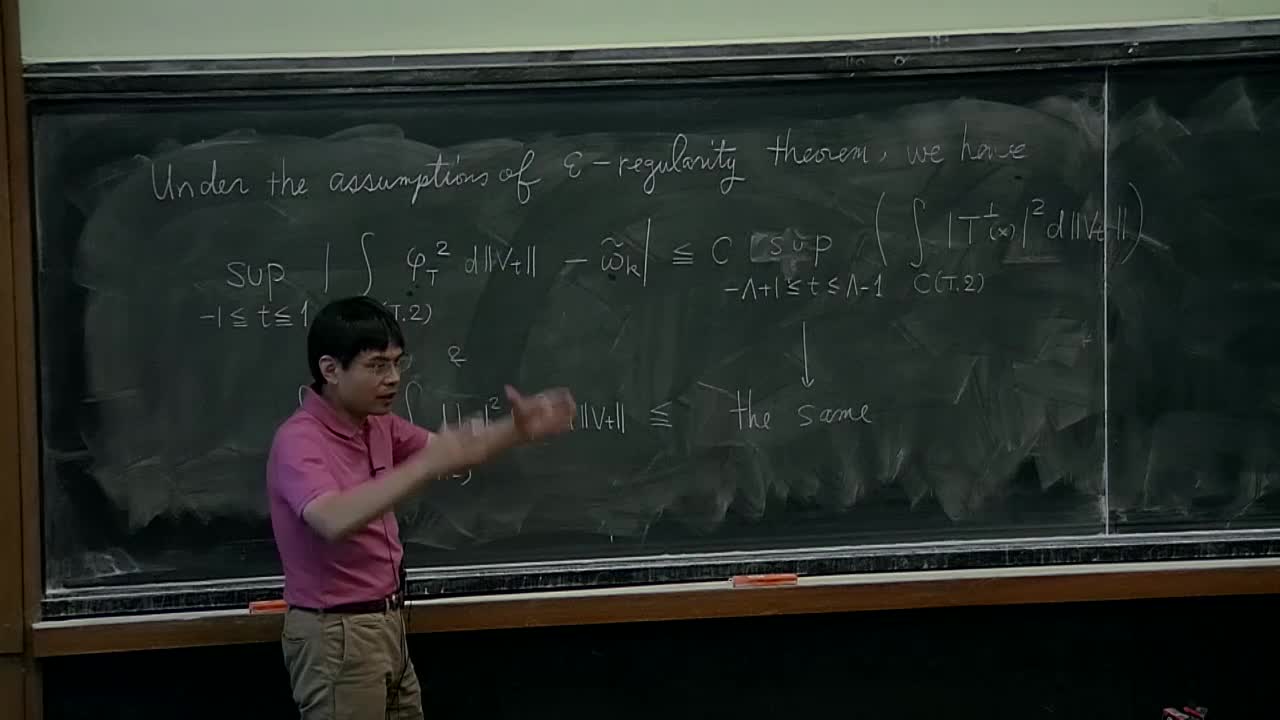Notice
Yoshihiro Tonegawa - Analysis on the mean curvature flow and the reaction-diffusion approximation (Part 5)
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
The course covers two separate but closely related topics. The first topic is the mean curvature flow in the framework of GMT due to Brakke. It is a flow of varifold moving by the generalized mean curvature. Starting from a quick review on the necessary tools and facts from GMT and the definition of the Brakke mean curvature flow, I will give an overview on the proof of the local regularity theorem. The second topic is the reaction-diffusion approximation of phase boundaries with key words such as the Modica-Mortola functional and the Allen-Cahn equation. Their singular perturbation problems are related to objects such as minimal surfaces and mean curvature flows in the framework of GMT.
Thème
Documentation
Liens
Dans la même collection
-
Matthias Röger - A curvature energy for bilayer membranes
RöGER Matthias
A curvature energy for bilayer membranes
-
Giovanni Pisante - Duality approach to a variational problem involving a polyconvex integrand
PISANTE Giovanni
Duality approach to a variational problem involving a polyconvex integrand
-
Neshan Wickramasereka - Stability in minimal and CMC hypersurfaces
WICKRAMASEKARA Neshan
indisponible
-
-
Free discontinuity problems and Robin boundary conditions
GIACOMINI Alessandro
par Alessandro Giacomini, université de Brescia
-
-
-
-
-
-
-
Avec les mêmes intervenants et intervenantes
-
Yoshihiro Tonegawa - Analysis on the mean curvature flow and the reaction-diffusion approximation (…
TONEGAWA Yoshihiro
The course covers two separate but closely related topics. The first topic is the mean curvature flow in the framework of GMT due to Brakke. It is a flow of varifold moving by the generalized
-
Yoshihiro Tonegawa - Analysis on the mean curvature flow and the reaction-diffusion approximation (…
TONEGAWA Yoshihiro
The course covers two separate but closely related topics. The first topic is the mean curvature flow in the framework of GMT due to Brakke. It is a flow of varifold moving by the generalized
-
Yoshihiro Tonegawa - Analysis on the mean curvature flow and the reaction-diffusion approximation (…
TONEGAWA Yoshihiro
The course covers two separate but closely related topics. The first topic is the mean curvature flow in the framework of GMT due to Brakke. It is a flow of varifold moving by the generalized
-
Yoshihiro Tonegawa - Analysis on the mean curvature flow and the reaction-diffusion approximation (…
TONEGAWA Yoshihiro
The course covers two separate but closely related topics. The first topic is the mean curvature flow in the framework of GMT due to Brakke. It is a flow of varifold moving by the generalized
Sur le même thème
-
"Le mathématicien Petre (Pierre) Sergescu, historien des sciences, personnalité du XXe siècle"
HERLéA Alexandre
Alexandre HERLEA est membre de la section « Sciences, histoire des sciences et des techniques et archéologie industrielle » du CTHS. Professeur émérite des universités, membre effectif de l'Académie
-
Webinaire sur la rédaction des PGD
LOUVET Violaine
Rédaction des Plans de Gestion de Données (PGD) sous l’angle des besoins de la communauté mathématique.
-
Alexandre Booms : « Usage de matériel pédagogique adapté en géométrie : une transposition à interro…
« Usage de matériel pédagogique adapté en géométrie : une transposition à interroger ». Alexandre Booms, doctorant (Université de Reims Champagne-Ardenne - Cérep UR 4692)
-
C. Li - Classifying sufficiently connected PSC manifolds in 4 and 5 dimensions
LI Chao
In this talk, I will discuss some recent developments on the topology of closed manifolds admitting Riemannian metrics of positive scalar curvature. In particular, we will prove if a closed PSC
-
Y. Lai - A family of 3d steady gradient Ricci solitons that are flying wings
LAI Yi
We find a family of 3d steady gradient Ricci solitons that are flying wings. This verifies a conjecture by Hamilton. For a 3d flying wing, we show that the scalar curvature does not vanish at
-
T. Ozuch - Noncollapsed degeneration and desingularization of Einstein 4-manifolds
OZUCH Tristan
We study the noncollapsed singularity formation of Einstein 4-manifolds. We prove that any smooth Einstein 4-manifold close to a singular one in a mere Gromov-Hausdorff (GH) sense is the result
-
D. Tewodrose - Limits of Riemannian manifolds satisfying a uniform Kato condition
TEWODROSE David
Presentation of a joint work with G. Carron and I. Mondello where we study Kato limit spaces.
-
A. Mondino - Time-like Ricci curvature bounds via optimal transport
MONDINO Andrea
The goal of the talk is to present a recent work in collaboration with Cavalletti (SISSA) on optimal transport in Lorentzian synthetic spaces. The aim is to set up a “Lorentzian analog” of the
-
M. Lesourd - Positive Scalar Curvature on Noncompact Manifolds and the Positive Mass Theorem
LESOURD Martin
The study of positive scalar curvature on noncompact manifolds has seen significant progress in the last few years. A major role has been played by Gromov's results and conjectures, and in
-
J. Wang - Topological rigidity and positive scalar curvature
WANG Jian
In this talk, we shall describe some topological rigidity and its relationship with positive scalar curvature. Precisely, we will present a proof that a complete contractible 3-manifold with
-
R. Perales - Recent Intrinsic Flat Convergence Theorems
PERALES Raquel
Théorèmes récents de convergence plane intrinsèque
-
J. Fine - Knots, minimal surfaces and J-holomorphic curves
FINE Joël
I will describe work in progress, parts of which are joint with Marcelo Alves. Let L be a knot or link in the 3-sphere. I will explain how one can count minimal surfaces in hyperbolic 4-space
