Cours/Séminaire
Ecoles d'été
282 Cours
Phong NGUYEN - Recent progress on lattices's computations 2
This is an introduction to the mysterious world of lattice algorithms, which have found many applications in computer science, notably in cryptography. We will explain how lattices are represented by
Aurel PAGE - Cohomology of arithmetic groups and number theory: geometric, asymptotic and computati…
In this lecture series, the first part will be dedicated to cohomology of arithmetic groups of lower ranks (e.g., Bianchi groups), their associated geometric models (mainly from hyperbolic geometry)
Tobias Moede - Coclass theory for nilpotent associative algebras
The coclass of a finite p-group of order p^n and class c is defined as n-c. Using coclass as the primary invariant in the investigation of finite p-groups turned out to be a very fruitful approach.
Zachary Himes - On not the rational dualizing module for $\text{Aut}(F_n)$
Bestvina--Feighn proved that $\text{Aut}(F_n)$ is a rational duality group, i.e. there is a $\mathbb{Q}[\text{Aut}(F_n)]$-module, called the rational dualizing module, and a form of Poincar\'e duality
Alexander HULPKE - Computational group theory, cohomology of groups and topological methods 5
The lecture series will give an introduction to the computer algebra system GAP, focussing on calculations involving cohomology. We will describe the mathematics underlying the algorithms, and how to
Alexander HULPKE - Computational group theory, cohomology of groups and topological methods 4
The lecture series will give an introduction to the computer algebra system GAP, focussing on calculations involving cohomology. We will describe the mathematics underlying the algorithms, and how to
Gabriele NEBE - Lattices, Perfects lattices, Voronoi reduction theory, modular forms, computations …
The talks of Coulangeon will introduce the notion of perfect, eutactic and extreme lattices and the Voronoi's algorithm to enumerate perfect lattices (both Eulcidean and Hermitian). The talk of Nebe
Oussama Hamza - Hilbert series and mild groups
Let $p$ be an odd prime number and $G$ a finitely generated pro-$p$ group. Define $I(G)$ the augmentation ideal of the group algebra of $G$ over $F_p$ and define the Hilbert series of $G$ by: $G(t):
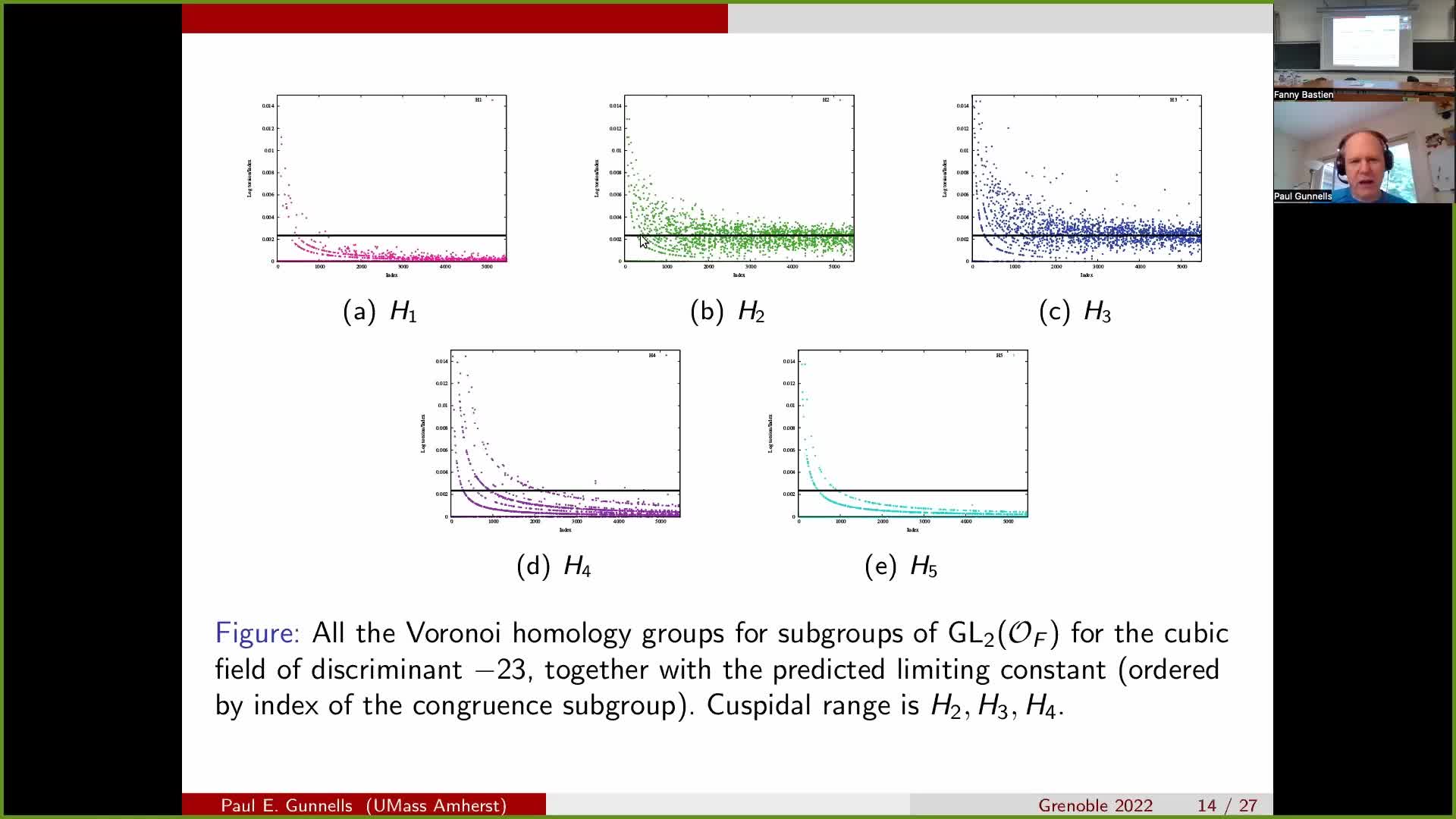
Paul GUNNELLS - Cohomology of arithmetic groups and number theory: geometric, asymptotic and comput…
In this lecture series, the first part will be dedicated to cohomology of arithmetic groups of lower ranks (e.g., Bianchi groups), their associated geometric models (mainly from hyperbolic geometry)
Paul GUNNELLS - Cohomology of arithmetic groups and number theory: geometric, asymptotic and comput…
In this lecture series, the first part will be dedicated to cohomology of arithmetic groups of lower ranks (e.g., Bianchi groups), their associated geometric models (mainly from hyperbolic geometry)
Paul GUNNELLS - Cohomology of arithmetic groups and number theory: geometric, asymptotic and comput…
In this lecture series, the first part will be dedicated to cohomology of arithmetic groups of lower ranks (e.g., Bianchi groups), their associated geometric models (mainly from hyperbolic geometry)
Paul GUNNELLS - Cohomology of arithmetic groups and number theory: geometric, asymptotic and comput…
In this lecture series, the first part will be dedicated to cohomology of arithmetic groups of lower ranks (e.g., Bianchi groups), their associated geometric models (mainly from hyperbolic geometry)
Paul GUNNELLS - Cohomology of arithmetic groups and number theory: geometric, asymptotic and comput…
In this lecture series, the first part will be dedicated to cohomology of arithmetic groups of lower ranks (e.g., Bianchi groups), their associated geometric models (mainly from hyperbolic geometry)
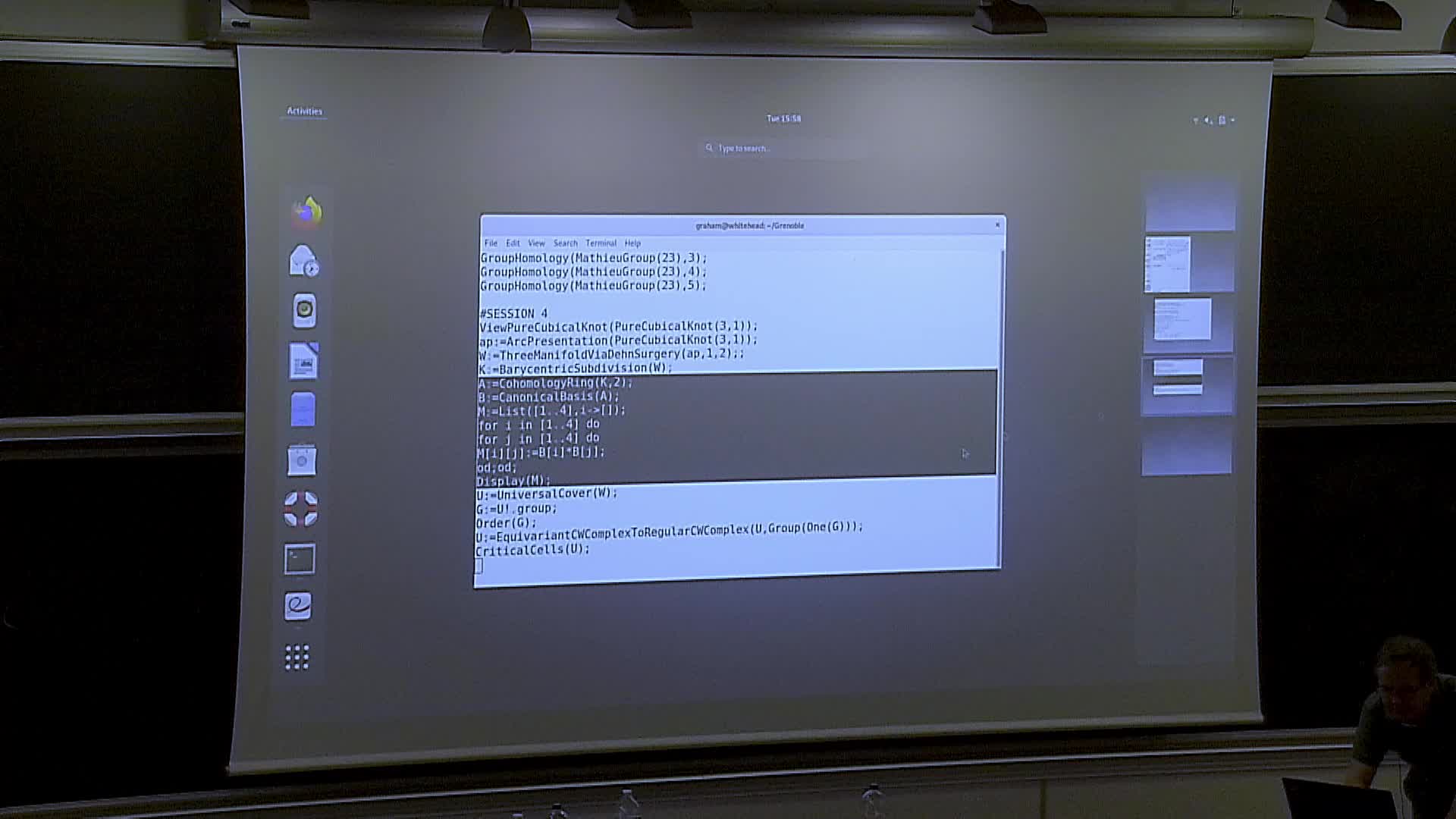
Graham ELLIS - Computational group theory, cohomology of groups and topological methods 3
The lecture series will give an introduction to the computer algebra system GAP, focussing on calculations involving cohomology. We will describe the mathematics underlying the algorithms, and how to
Philippe ELBAZ - Cohomology of arithmetic groups and number theory: geometric, asymptotic and comp…
In this lecture series, the first part will be dedicated to cohomology of arithmetic groups of lower ranks (e.g., Bianchi groups), their associated geometric models (mainly from hyperbolic geometry)
Graham ELLIS - Computational group theory, cohomology of groups and topological methods 1
The lecture series will give an introduction to the computer algebra system GAP, focussing on calculations involving cohomology. We will describe the mathematics underlying the algorithms, and how to
Philippe ELBAZ - Cohomology of arithmetic groups and number theory: geometric, asymptotic and compu…
In this lecture series, the first part will be dedicated to cohomology of arithmetic groups of lower ranks (e.g., Bianchi groups), their associated geometric models (mainly from hyperbolic geometry)
Graham ELLIS - Computational group theory, cohomology of groups and topological methods 2
The lecture series will give an introduction to the computer algebra system GAP, focussing on calculations involving cohomology. We will describe the mathematics underlying the algorithms, and how to
Bettina EICK - Computational group theory, cohomology of groups and topological methods 4
The lecture series will give an introduction to the computer algebra system GAP, focussing on calculations involving cohomology. We will describe the mathematics underlying the algorithms, and how to
Bettina EICK - Computational group theory, cohomology of groups and topological methods 3
The lecture series will give an introduction to the computer algebra system GAP, focussing on calculations involving cohomology. We will describe the mathematics underlying the algorithms, and how to
Bettina EICK - Computational group theory, cohomology of groups and topological methods 5
The lecture series will give an introduction to the computer algebra system GAP, focussing on calculations involving cohomology. We will describe the mathematics underlying the algorithms, and how to
Renaud COULANGEON - Lattices, Perfects lattices, Voronoi reduction theory, modular forms, ... 2
The talks of Coulangeon will introduce the notion of perfect, eutactic and extreme lattices and the Voronoi's algorithm to enumerate perfect lattices (both Eulcidean and Hermitian). The talk of Nebe
Bettina EICK - Computational group theory, cohomology of groups and topological methods 1
The lecture series will give an introduction to the computer algebra system GAP, focussing on calculations involving cohomology. We will describe the mathematics underlying the algorithms, and how to
Angelica Babei - A family of $\phi$-congruence subgroups of the modular group
A family of $\phi$-congruence subgroups of the modular group
Calista Bernard - Applications of twisted homology operations for E_n-algebras
Applications of twisted homology operations for E_n-algebras
A. Lytchak - Convex subsets in generic manifolds
In the talk I would like to discuss some statements and questions about convex subsets and convex hulls in generic Riemannian manifolds of dimension at least 3. The statements, obtained jointly
C. Sormani - Intrinsic Flat and Gromov-Hausdorff Convergence 3
We introduce various notions of convergence of Riemannian manifolds and metric spaces. We then survey results and open questions concerning the limits of sequences of Riemannian manifolds with
C. Sormani - Intrinsic Flat and Gromov-Hausdorff Convergence 2
We introduce various notions of convergence of Riemannian manifolds and metric spaces. We then survey results and open questions concerning the limits of sequences of Riemannian manifolds with
C. Sormani - Intrinsic Flat and Gromov-Hausdorff Convergence 4
We introduce various notions of convergence of Riemannian manifolds and metric spaces. We then survey results and open questions concerning the limits of sequences of Riemannian manifolds with
C. Sormani - Intrinsic Flat and Gromov-Hausdorff Convergence 1
We introduce various notions of convergence of Riemannian manifolds and metric spaces. We then survey results and open questions concerning the limits of sequences of Riemannian manifolds with