2: McEliece Cryptosystem

Descriptif
Tables of contents
2.1. Formal Definition
2.2. Security-Reduction Proof
2.3. McEliece Assumptions
2.4. Notions of Security
2.5. Critical Attacks - Semantic Secure Conversions
2.6. Reducing the Key Size
2.7. Reducing the Key Size - LDPC codes
2.8. Reducing the Key Size - MDPC codes
2.9. Implementation
Vidéos
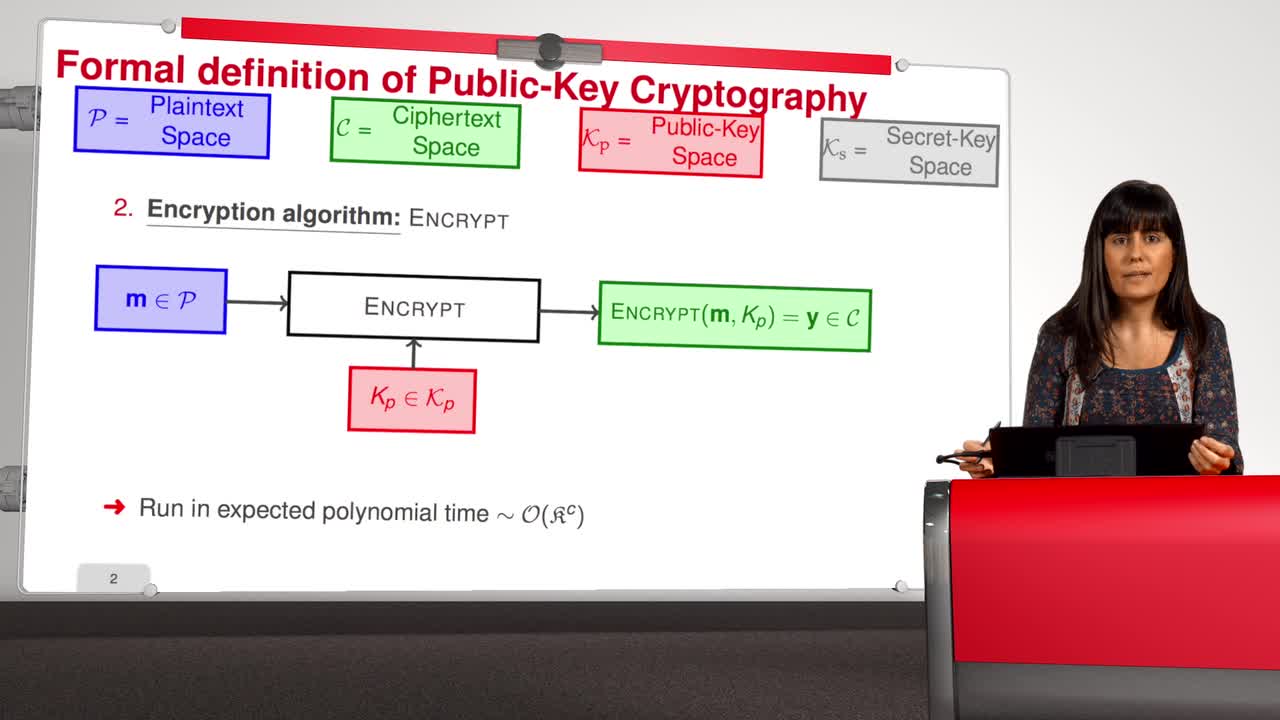
2.1. Formal Definition
Welcome to the second week of this MOOC entitled Code-Based Cryptography. This week, we will talk in detail about the McEliece cryptosystem. First, in this session, we will describe formally the
2.2. Security-Reduction Proof
Welcome to the second session. We will talk about the security-reduction proof. The security of a given cryptographic algorithm is reduced to the security of a known hard problem. To prove that a
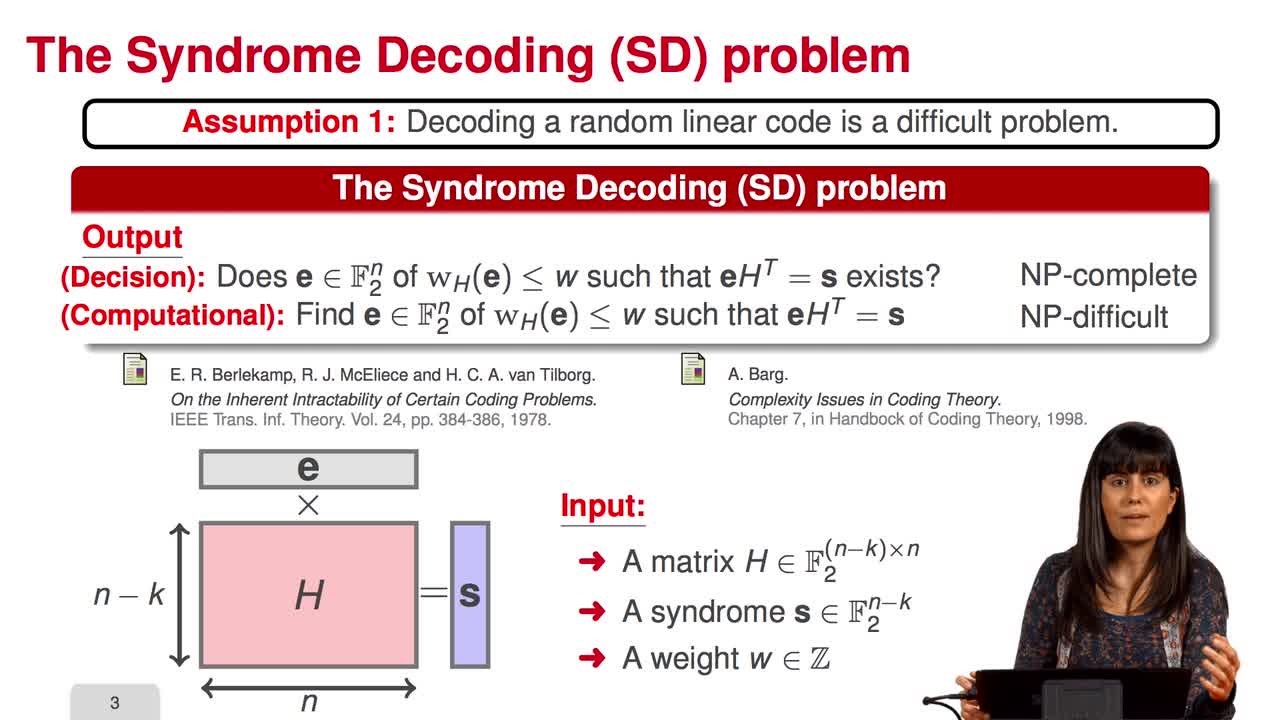
2.3. McEliece Assumptions
In this session, we will talk about McEliece assumptions. The security of the McEliece scheme is based on two assumptions as we have already seen: the hardness of decoding a random linear code and
2.4. Notions of Security
In this session, we will study the notion of security of public-key scheme. A public-key scheme is one-way if the probability of success of any adversary running in polynomial time is negligible.
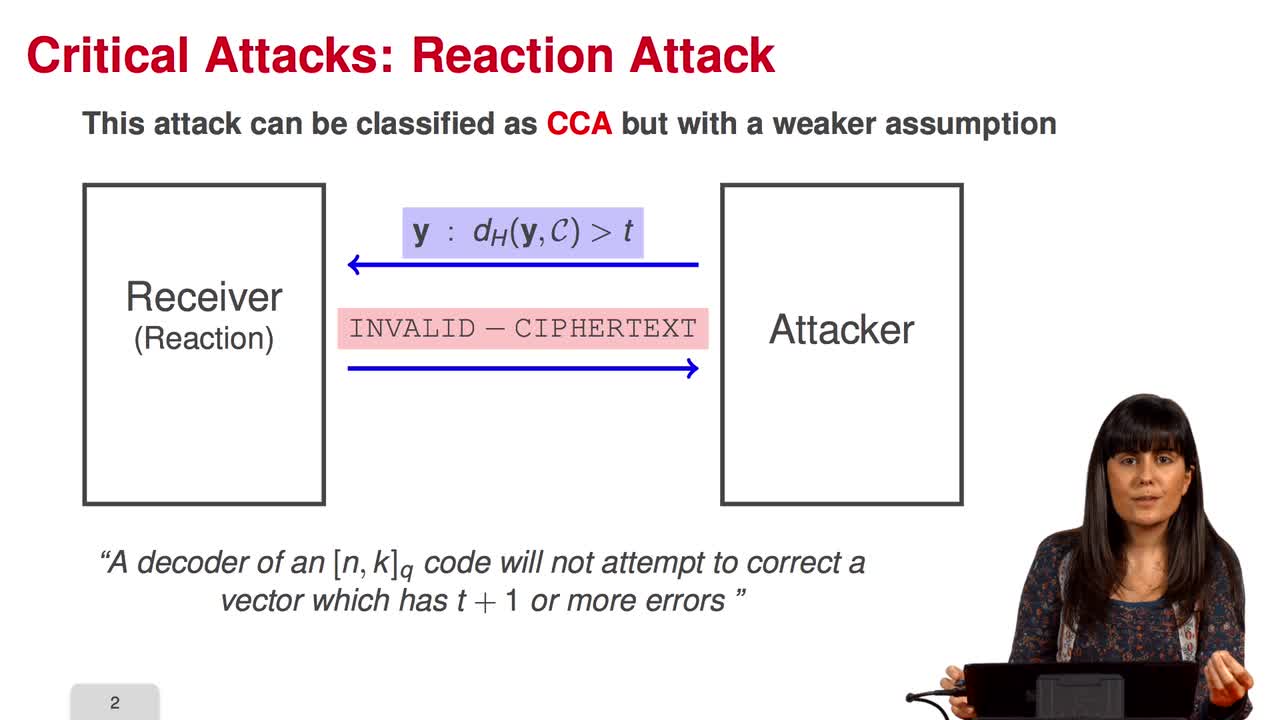
2.5. Critical Attacks - Semantic Secure Conversions
In this session, we will study critical attacks against the public-key cryptosystem. The partial knowledge on the plaintext reduces drastically the computational cost of the attack to the McEliece
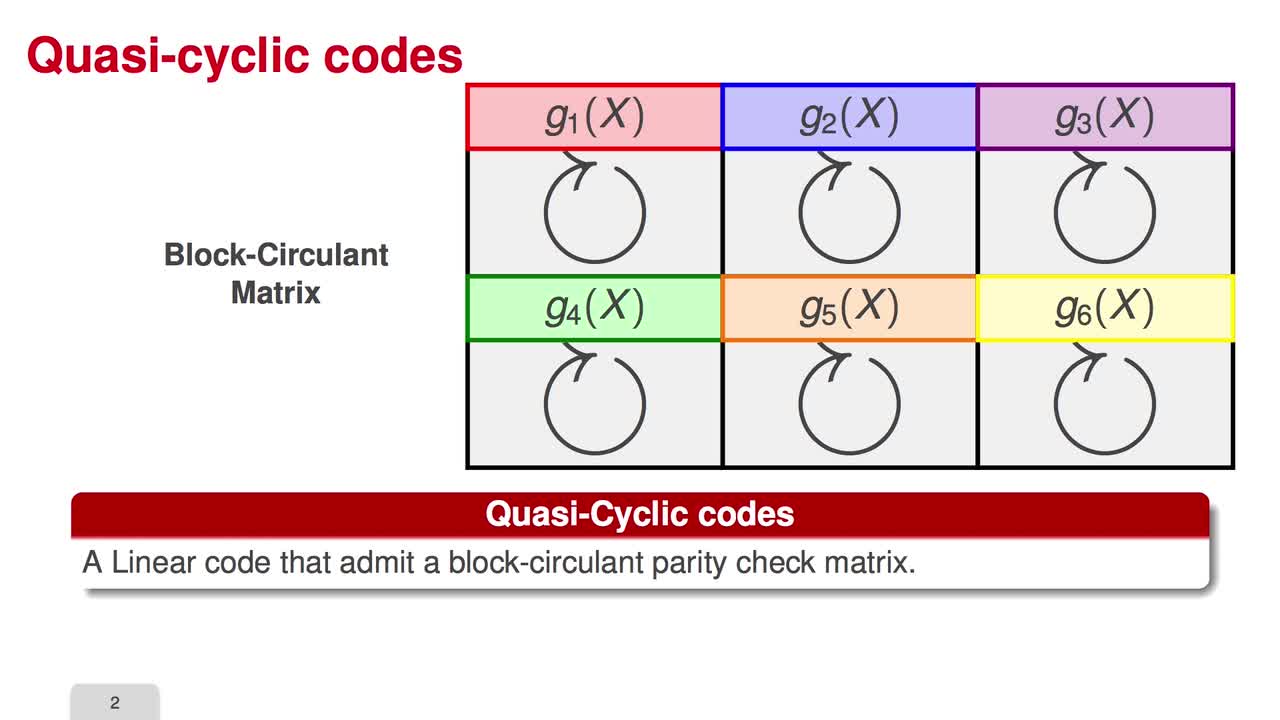
2.6. Reducing the Key Size
In the next three sessions, I will explain how to reduce the key size of code-based cryptosystem. Circulant matrices are the central point in many attempts to reduce the key size of code-based
2.7. Reducing the Key Size - LDPC codes
LDPC codes have an interesting feature: they are free of algebraic structure. We will study in detail this proposal for the McEliece cryptosystem in this session. LDPC codes were originally
2.8. Reducing the Key Size - MDPC codes
This is the last session where we will talk about reducing the key size. Here we will introduce the MDPC codes. In 2012, the MDPC codes were proposed for the McEliece schemes. An MDPC code is a
2.9. Implementation
This is the last session of the second week. The cryptography community has different options for using public key cryptosystems, among others, they have RSA or DSA. But … McEliece has the same
Intervenants et intervenantes
Auteur d'une thèse en mathématiques et informatique à l'Ecole polytechnique de Paris
Chercheuse à la faculté des sciences de l'université de La Laguna. Spécialités : code, cryptograhie et algèbre informatique (2015)
Enseignant chercheur en informatique à l'INRIA. Thèmes de recherche : Codes correcteurs d'erreurs et Cryptographie.