Sendrier, Nicolas (19..-....)
- Analyse numérique
- Cryptographie
- Mathématiques
- Théorie de l'information
- Algorithmes
- données dans les systèmes informatiques
- cryptographie
- algèbre linéaire
- chiffrement à clé publique
- cryptage des données
- données dans les systèmes informatiques
- cryptographie
- algèbre linéaire
- chiffrement à clé publique
- cryptage des données
Vidéos
4.5. Error-Correcting Pairs
We present in this session a general decoding method for linear codes. And we will see it in an example. Let C be a generalized Reed-Solomon code of dimension k associated to the pair (c, d). Then,
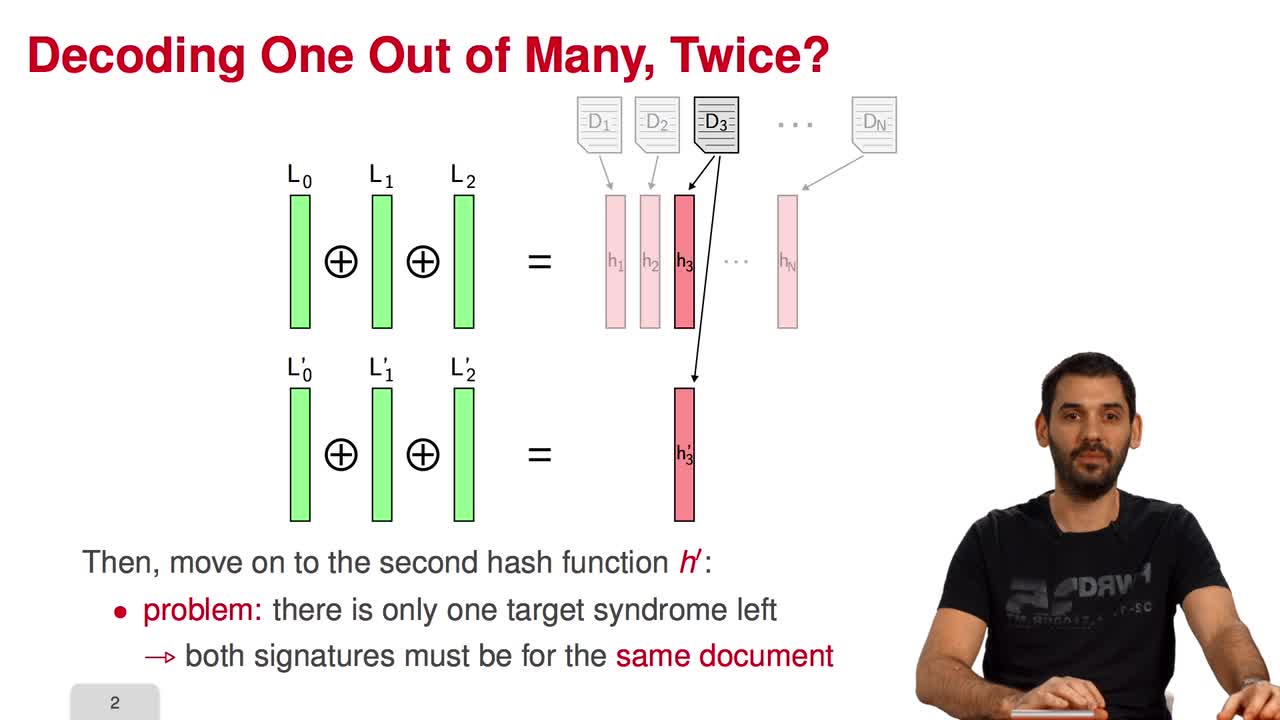
5.4. Parallel-CFS
In this session, I will present a variant of the CFS signature scheme called parallel-CFS. We start from a simple question: what happens if you try to use two different hash functions and compute
4.8. Attack against Algebraic Geometry codes
In this session, we will present an attack against Algebraic Geometry codes (AG codes). Algebraic Geometry codes is determined by a triple. First of all, an algebraic curve of genus g, then a n
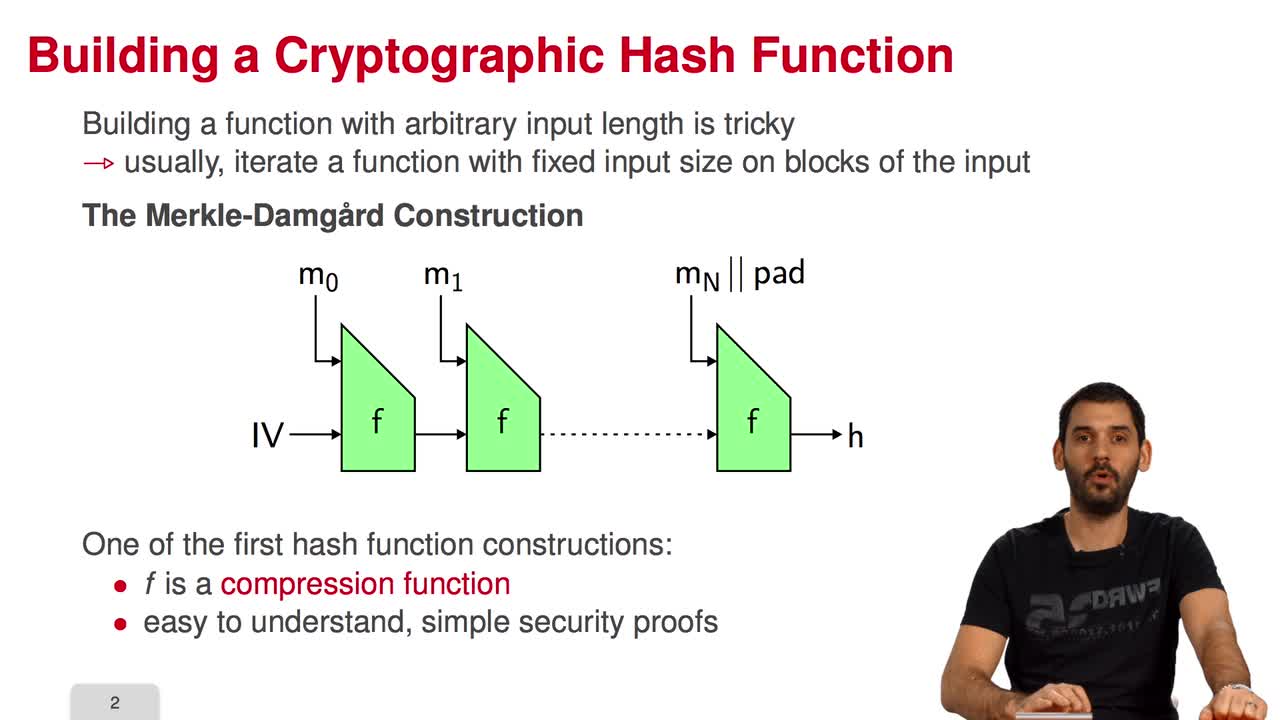
5.7. The Fast Syndrome-Based (FSB) Hash Function
In the last session of this week, we will have a look at the FSB Hash Function which is built using the one-way function we saw in the previous session. What are the requirements for a
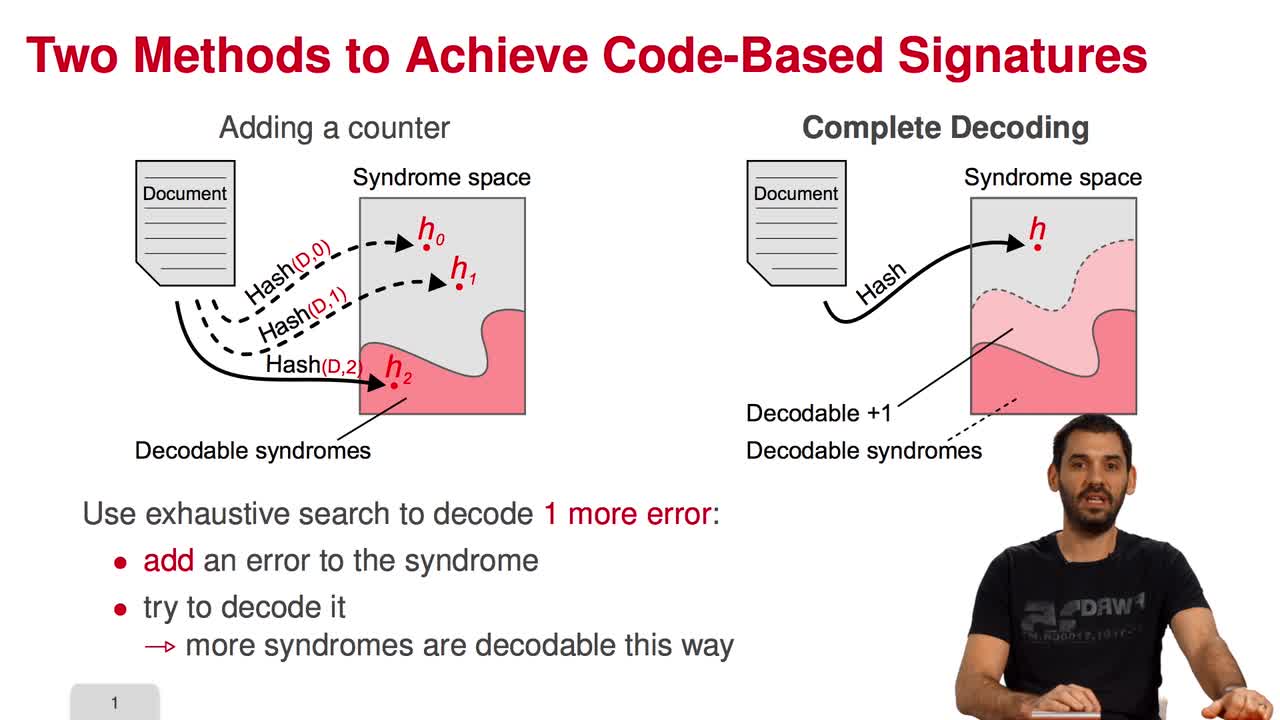
5.2. The Courtois-Finiasz-Sendrier (CFS) Construction
In this session, I am going to present the Courtois-Finiasz-Sendrier Construction of a code-based digital signature. In the previous session, we have seen that it is impossible to hash a document
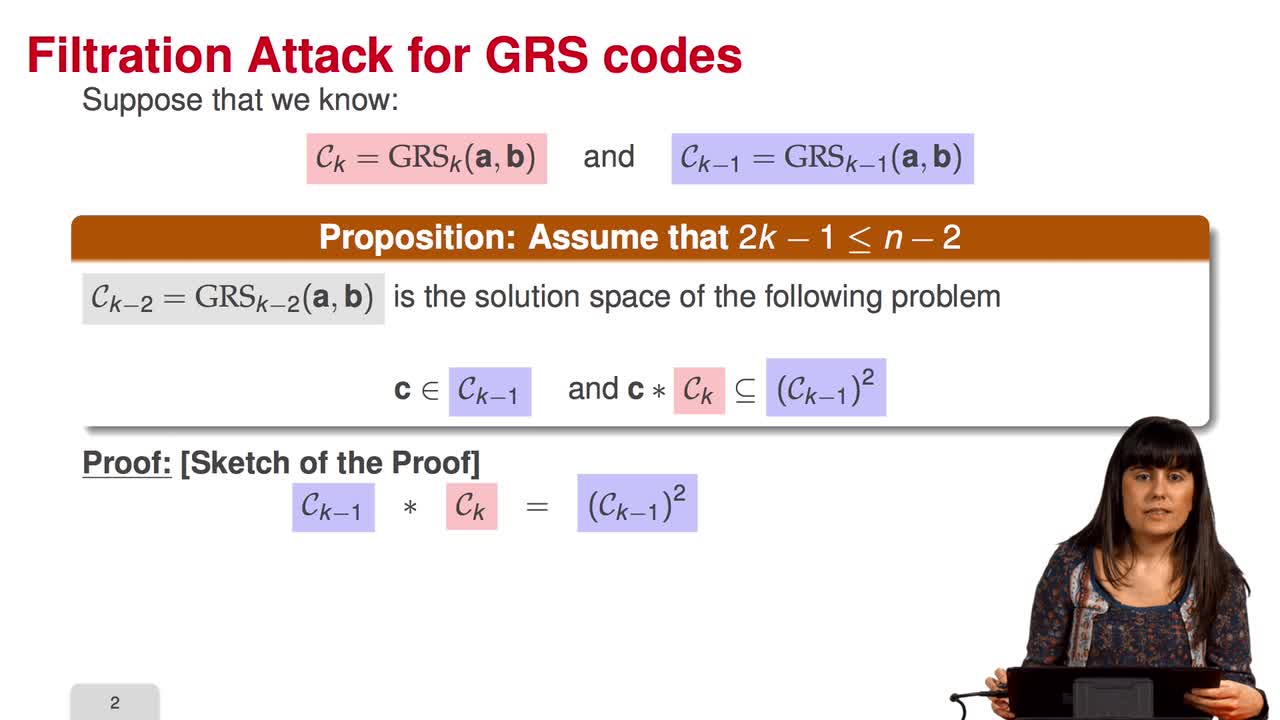
4.6. Attack against GRS codes
In this session we will discuss the proposal of using generalized Reed-Solomon codes for the McEliece cryptosystem. As we have already said, generalized Reed-Solomon codes were proposed in 1986 by
5.5. Stern’s Zero-Knowledge Identification Scheme
In this session, we are going to have a look at Stern’s Zero-Knowledge Identification Scheme. So, what is a Zero-Knowledge Identification Scheme? An identification scheme allows a prover to prove
4.9. Goppa codes still resist
All the results that we have seen this week doesn't mean that code based cryptography is broken. So in this session we will see that Goppa code still resists to all these attacks. So recall that
4.4. Attack against subcodes of GRS codes
In this session, we will talk about using subcodes of a Generalized Reed–Solomon code for the McEliece Cryptosystem. Recall that to avoid the attack of Sidelnikov and Shestakov, Berger and
5.3. Attacks against the CFS Scheme
In this session, we will have a look at the attacks against the CFS signature scheme. As for public-key encryption, there are two kinds of attacks against signature schemes. First kind of attack is
4.7. Attack against Reed-Muller codes
In this session, we will introduce an attack against binary Reed-Muller codes. Reed-Muller codes were introduced by Muller in 1954 and, later, Reed provided the first efficient decoding algorithm
5.6. An Efficient Provably Secure One-Way Function
In this session, we are going to see how to build an efficient provably secure one-way function from coding theory. As you know, a one-way function is a function which is simple to evaluate and