3: Message Attacks (ISD)

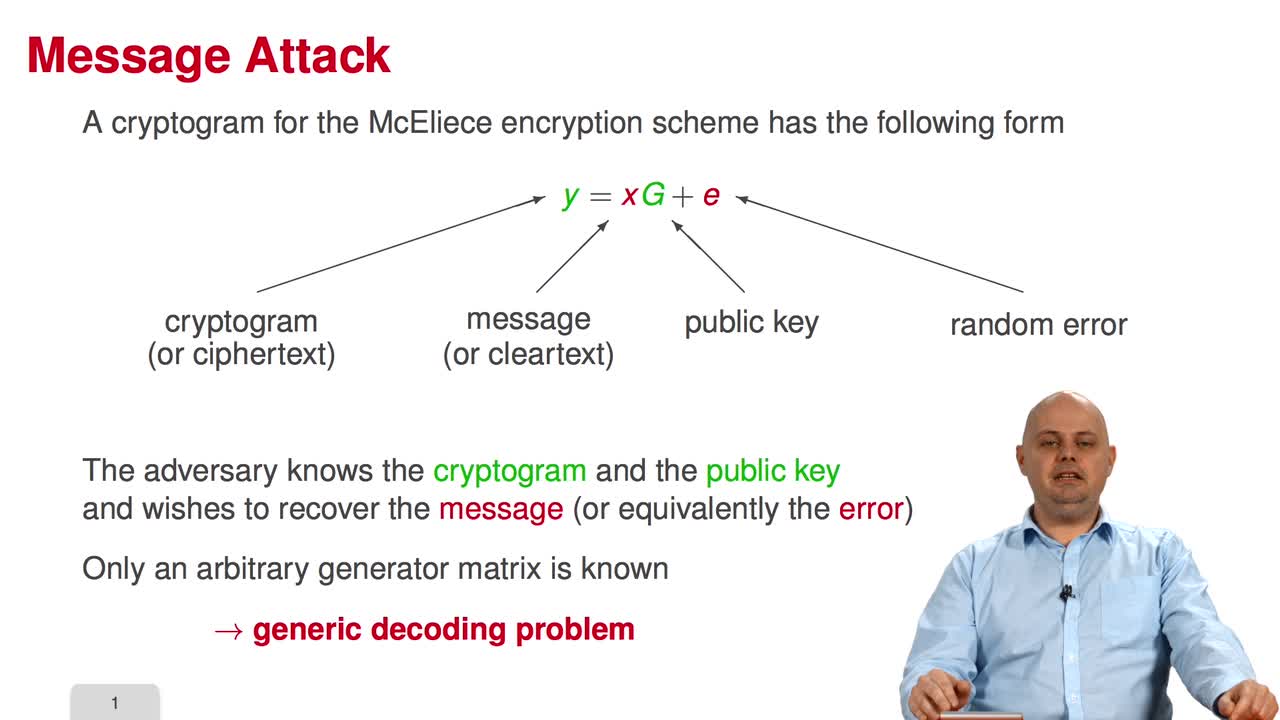
Welcome to the third week of the MOOC on code-based cryptography. This week, we will learn about message attacks. Among the ten sessions of this week, the first six will present the most essential

In this session, I will detail two combinatorial solutions to the decoding problem. The first one is the Exhaustive Search. To find our w columns, we will simply enumerate all the tuples j1 to jw

In this third session, we will present the most important concept of the week: Information Set Decoding. The problem of decoding is not only a combinatorial problem. Because we are dealing with

In this session, I will present the main technique to make the analysis of the various algorithms presented in this course. So, Information Set Decoding refers to a family of algorithms which is

In this fifth session, we will study a variant of information set decoding proposed by Lee and Brickell. So, the main idea consists in relaxing the Prange algorithm to amortize the cost of the

In this session, we will present the Stern algorithm for decoding. In fact, the idea is to combine two algorithms that we have seen before, the Lee and Brickell algorithm and the Birthday Decoding.

So, with the session 7 we are entering the most advanced part of that course. The idea of what I called the  Improved Birthday Decoding is to use the so-called "representation technique" introduced

Now in session 8, we will present yet another evolution of information set decoding. Before presenting this improvement, we will first improve the Birthday Decoding algorithm what I call a Further

The session nine is devoted to the application of the Generalized Birthday Algorithm to decoding. The Generalized Birthday Algorithm was presented by David Wagner in 2002, in a more general

The final session of this week is devoted to Decoding One Out of Many. Decoding One Out of Many is interested in solving the following variant of Syndrome Decoding. In this variant, the only