Notice
Supercritical percolation on finite transitive graphs
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
In Bernoulli bond percolation, each edge of some graph are chosen to be either deleted or retained independently at random with retention probability p. For many large finite graphs, there is a phase transition such that if p is sufficiently large then there exists a giant cluster whose volume is proportional to that of the graph with high probability. We prove that in this phase the giant cluster must be unique with high probability: this was previously known only for tori and expander graphs via methods specific to those cases. Joint work with Philip Easo.
Intervention / Responsable scientifique
Thème
Dans la même collection
-
Rotational invariance of planar percolation
OulamaraMendesWe prove the asymptotic rotational invariance of the critical FK-percolation model on the square lattice with any cluster-weight between 1 and 4.
-
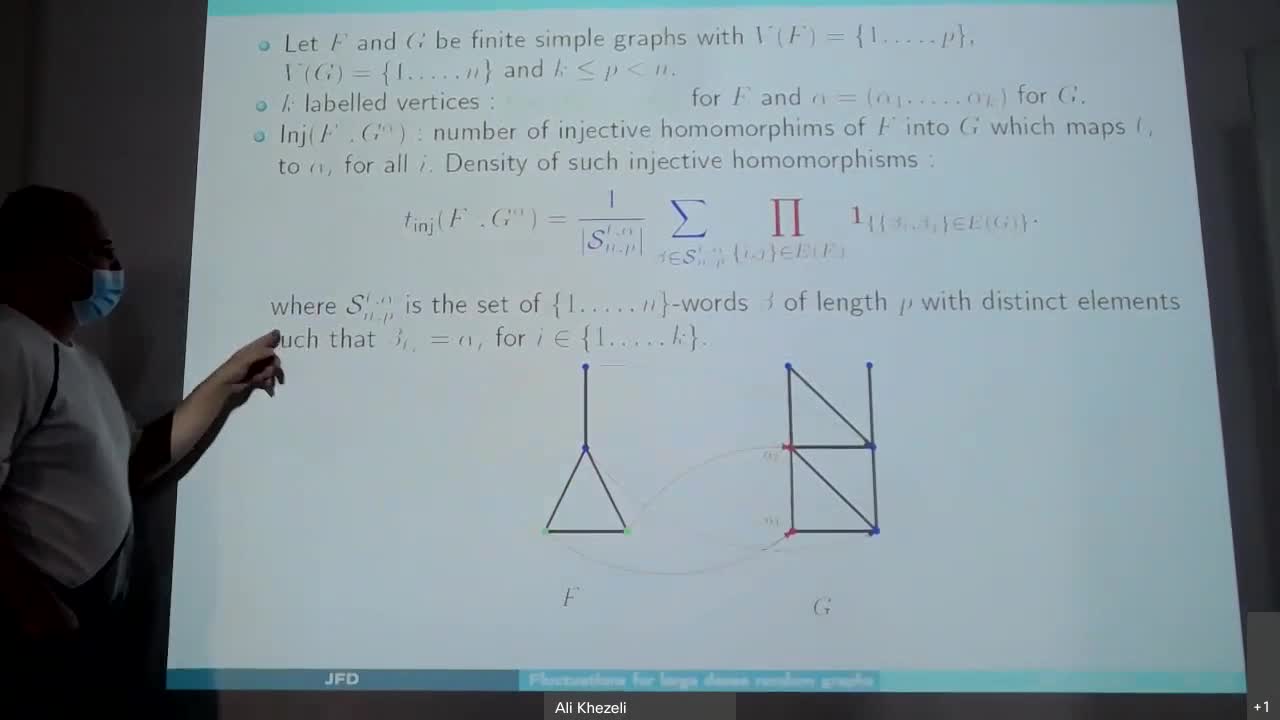
Asymptotic for the cumulative distribution function of the degrees and homomorphism densities for r…
DelmasJean-FrançoisWe shall first recall the limits of large dense random networks, also called graphon, as well as the construction of (random) graphs sampled from graphon.
Sur le même thème
-
Bruit, erreur, anomalie et incertitude dans les données-PUDD
RossiFabriceLes données collectées sont systématiquement soumises à des perturbations de diverses natures, depuis le bruit de mesure de capteurs jusqu’aux erreurs de saisie.
-
Combinatorial maps in high genus
LoufBaptisteCombinatorial maps are a model of discrete geometry: they are surfaces made by gluing polygons along their sides, or equivalently, graphs drawn on surfaces. In this talk, I'll focus on the study of
-
Do there exist expanders with non-negative curvature ?
SalezJustinIn this talk I will briefly recall the framework of local weak limits of finite graphs introduced by I. Benjamini and O. Schramm
-
Tail bounds for detection times in mobile hyperbolic graphs
MitscheDieterMotivated by Krioukov et al.'s model of random hyperbolic graphs for real-world networks, and inspired by the analysis of a dynamic model of graphs in Euclidean space by Peres et al., we introduce a
-
Sofic entropy of processes on infinite random trees
BordenaveCharlesThis is a joint work with Agnes Backhausz et Balasz Szegedy. We define a natural notion of micro-state entropy...
-
Online matching for the multiclass Stochastic Block Model
SOPRANO LOTONahuelA matching in a graph is a set of edges that do not share endpoints. Developing algorithms that find large matchings is an important problem. An algorithm is said to be online if it has to construct
-
Critical cluster cascades
KirchnerMatthiasWe consider a sequence of Poisson cluster point processes...
-
Point processes on higher rank symmetric spaces and their cost
MellickSamuelCost is a natural invariant associated to group actions and invariant point processes on symmetric spaces (such as Euclidean space and hyperbolic space). Informally, it measures how difficult it is to
-
Parallel server systems in extended heavy traffic
CastielEyalThe standard setting for studying parallel server systems (PSS) at the diffusion scale is based on the heavy traffic condition (HTC)...
-
The Maximal Agreement Subtree problem for random trees
BudzinskiThomasConsider two binary trees whose leaves are labelled from 1 to n.
-
An Improved Lower Bound on the Largest Common Subtree of Random Leaf-Labeled Binary Trees
KhezeliAliIt is known that the size of the largest common subtree...
-
Reversible Markov decision processes
AnantharamVenkatA Markov decision process is called reversible if for every stationary Markov control strategy the resulting Markov chain is reversible.