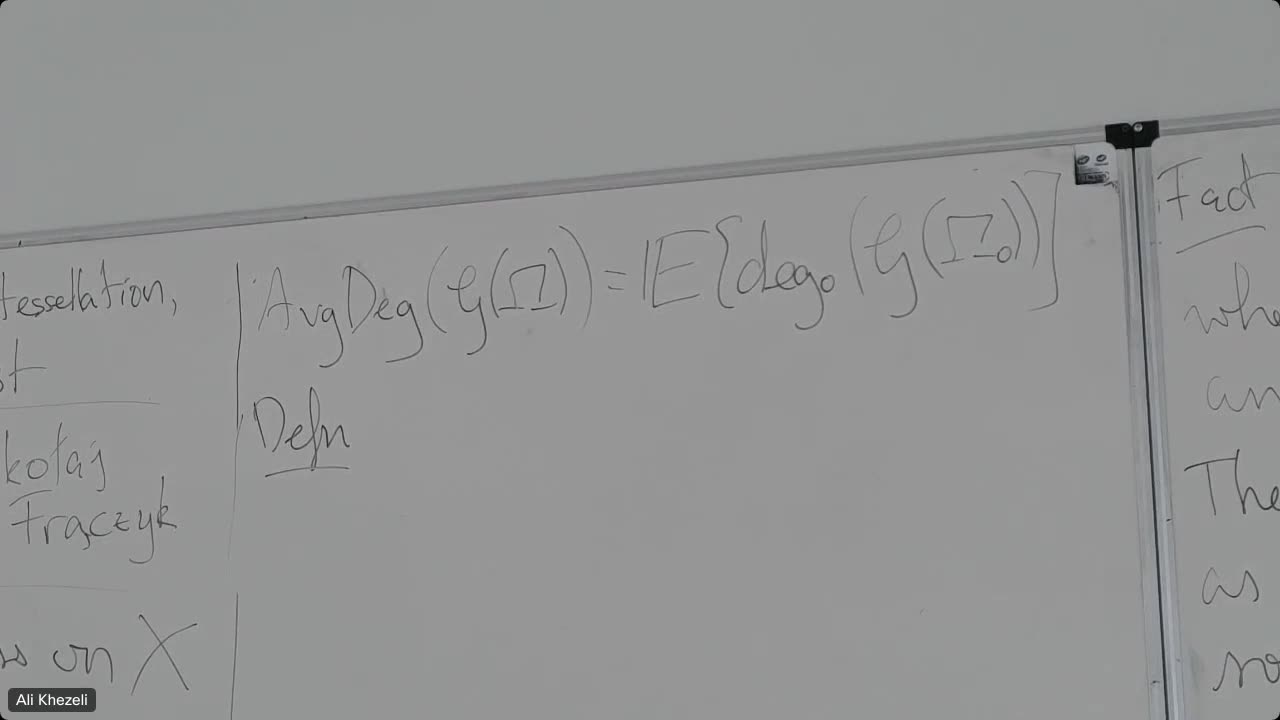Notice
Tail bounds for detection times in mobile hyperbolic graphs
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
Tail bounds for detection times in mobile hyperbolic graphs
Abstract: Motivated by Krioukov et al.'s model of random hyperbolic graphs for real-world networks, and inspired by the analysis of a dynamic model of graphs in Euclidean space by Peres et al., we introduce a dynamic model of hyperbolic graphs in which vertices are allowed to move according to a Brownian motion maintaining the distribution of vertices in hyperbolic space invariant. For different parameters of the speed of angular and radial motion, we analyze tail bounds for detection times of a fixed target and obtain a complete picture, for very different regimes, of how and when the target is detected: as a function of the time passed, we characterize the subset of the hyperbolic space where particles typically detecting the target are initially located.
We overcome several substantial technical difficulties not present in Euclidean space, and provide a complete picture on tail bounds. On the way, we obtain also new results for the time more general continuous processes with drift and reflecting barrier spent in certain regions, and we also obtain improved bounds for independent sums of Pareto random variables.
Joint work with Marcos Kiwi and Amitai Linker.
Intervention / Responsable scientifique
Thème
Dans la même collection
-
Combinatorial maps in high genus
LoufBaptisteCombinatorial maps are a model of discrete geometry: they are surfaces made by gluing polygons along their sides, or equivalently, graphs drawn on surfaces. In this talk, I'll focus on the study of
-
Do there exist expanders with non-negative curvature ?
SalezJustinIn this talk I will briefly recall the framework of local weak limits of finite graphs introduced by I. Benjamini and O. Schramm
-
Online matching for the multiclass Stochastic Block Model
SOPRANO LOTONahuelA matching in a graph is a set of edges that do not share endpoints. Developing algorithms that find large matchings is an important problem. An algorithm is said to be online if it has to construct
-
Critical cluster cascades
KirchnerMatthiasWe consider a sequence of Poisson cluster point processes...
-
Point processes on higher rank symmetric spaces and their cost
MellickSamuelCost is a natural invariant associated to group actions and invariant point processes on symmetric spaces (such as Euclidean space and hyperbolic space). Informally, it measures how difficult it is to
-
Parallel server systems in extended heavy traffic
CastielEyalThe standard setting for studying parallel server systems (PSS) at the diffusion scale is based on the heavy traffic condition (HTC)...
-
The Maximal Agreement Subtree problem for random trees
BudzinskiThomasConsider two binary trees whose leaves are labelled from 1 to n.
-
An Improved Lower Bound on the Largest Common Subtree of Random Leaf-Labeled Binary Trees
KhezeliAliIt is known that the size of the largest common subtree...
-
Reversible Markov decision processes
AnantharamVenkatA Markov decision process is called reversible if for every stationary Markov control strategy the resulting Markov chain is reversible.
-
The question of connectedness in the Free Uniform Spanning Forest
TimárÁdám DávidThe uniform measure on the set of all spanning trees of a finite graph is a classical object in probability.
-
Optimal Convex and Nonconvex Regularizers for a Data Source
O'ReillyElizaRegularization is a widespread technique used in statistical estimation problems that helps to capture low dimensional structure in the data and improve signal recovery.
-
Tropical convexity: application to linear programming and mean payoff games
GaubertStéphaneLinear programming, and more generally convex semialgebraic programming, makes sense...
Sur le même thème
-
Bruit, erreur, anomalie et incertitude dans les données-PUDD
RossiFabriceLes données collectées sont systématiquement soumises à des perturbations de diverses natures, depuis le bruit de mesure de capteurs jusqu’aux erreurs de saisie.
-
Combinatorial maps in high genus
LoufBaptisteCombinatorial maps are a model of discrete geometry: they are surfaces made by gluing polygons along their sides, or equivalently, graphs drawn on surfaces. In this talk, I'll focus on the study of
-
Do there exist expanders with non-negative curvature ?
SalezJustinIn this talk I will briefly recall the framework of local weak limits of finite graphs introduced by I. Benjamini and O. Schramm
-
Sofic entropy of processes on infinite random trees
BordenaveCharlesThis is a joint work with Agnes Backhausz et Balasz Szegedy. We define a natural notion of micro-state entropy...
-
Online matching for the multiclass Stochastic Block Model
SOPRANO LOTONahuelA matching in a graph is a set of edges that do not share endpoints. Developing algorithms that find large matchings is an important problem. An algorithm is said to be online if it has to construct
-
Critical cluster cascades
KirchnerMatthiasWe consider a sequence of Poisson cluster point processes...
-
Point processes on higher rank symmetric spaces and their cost
MellickSamuelCost is a natural invariant associated to group actions and invariant point processes on symmetric spaces (such as Euclidean space and hyperbolic space). Informally, it measures how difficult it is to
-
Parallel server systems in extended heavy traffic
CastielEyalThe standard setting for studying parallel server systems (PSS) at the diffusion scale is based on the heavy traffic condition (HTC)...
-
The Maximal Agreement Subtree problem for random trees
BudzinskiThomasConsider two binary trees whose leaves are labelled from 1 to n.
-
An Improved Lower Bound on the Largest Common Subtree of Random Leaf-Labeled Binary Trees
KhezeliAliIt is known that the size of the largest common subtree...
-
Reversible Markov decision processes
AnantharamVenkatA Markov decision process is called reversible if for every stationary Markov control strategy the resulting Markov chain is reversible.
-
The question of connectedness in the Free Uniform Spanning Forest
TimárÁdám DávidThe uniform measure on the set of all spanning trees of a finite graph is a classical object in probability.