Notice
Fluctuations of random convex interfaces
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
We consider the convex hull of a point set constituted with independent and uniformly distributed points in a smooth convex body K of R^d. We show that the rescaled maximal radial fluctuation as well as maximal facet area follow asymptotically a Gumbel extreme value distribution as the size of the input goes to infinity. These results rely in particular on the study of a so-called typical facet of the random polytope. In particular, the rates of convergence are similar to those observed for a large variety of random interfaces in probability theory (random cluster models, oriented random walks…). This is joint work with J. E. Yukich.
Intervention / Responsable scientifique
Thème
Dans la même collection
-
Sofic entropy of processes on infinite random trees
BordenaveCharlesThis is a joint work with Agnes Backhausz et Balasz Szegedy. We define a natural notion of micro-state entropy...
-
The bias of fluid approximation: Poisson equation, averaging methods and two-timescale processes
GastNicolasFluid approximation often provide a good tool to study a stochastic process.
-
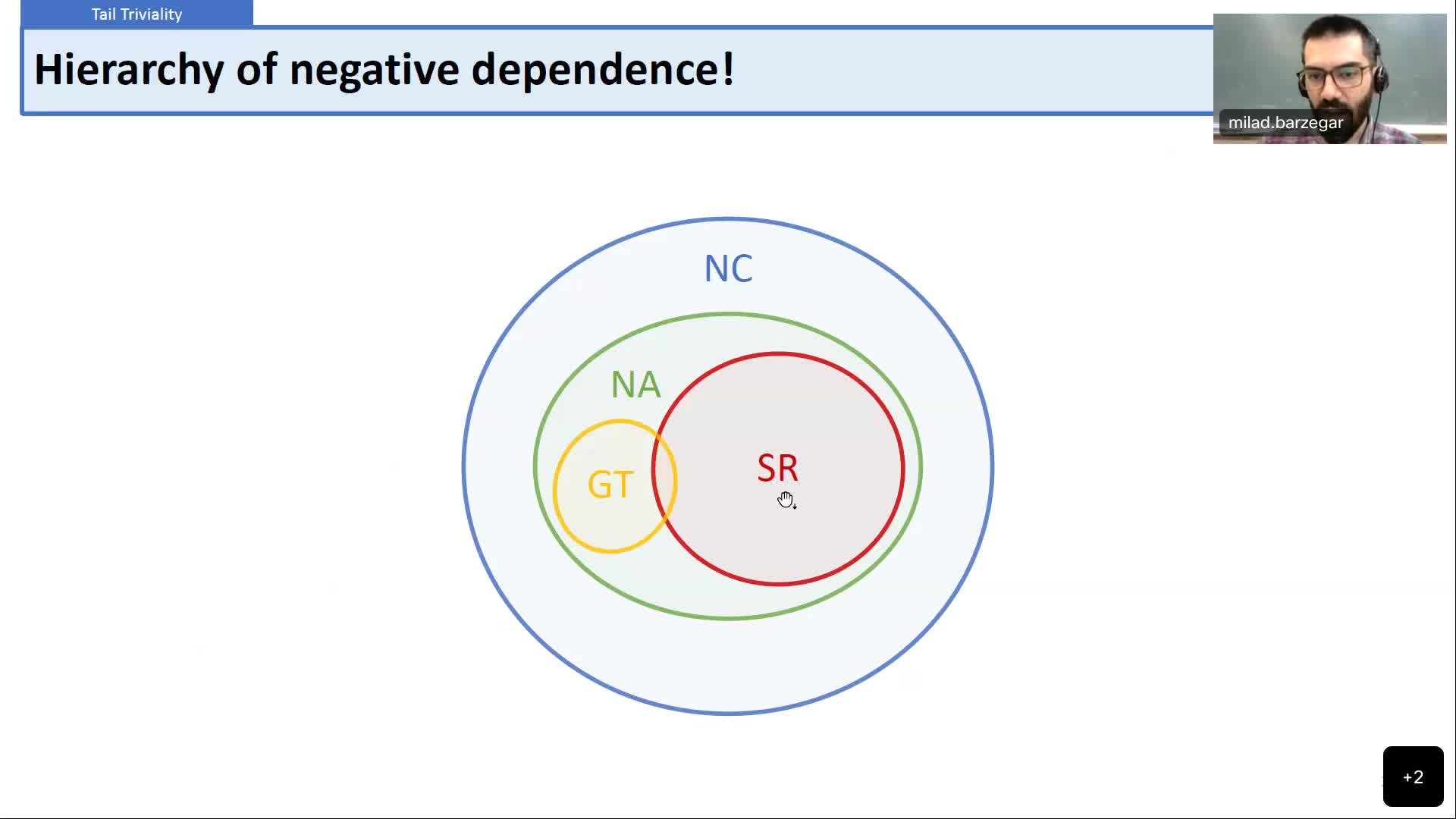
On the dependence structure of negatively dependent measures
Barzegar TouchaniMiladA major breakthrough in the theory of negatively dependent – i.e., repulsive – probability measure...
-
A Notion of Entropy for Sparse Marked Graphs and its Applications in Graphical Data Compression
DelgoshaPayamMany modern data sources arising from social networks, biological data, etc. are best viewed...
-
Propagation of chaos and Poisson Hypothesis for replica mean-field models of intensity-based neural…
DavydovMichelNeural computations arising from myriads of interactions between spiking neurons can be modeled as network dynamics with punctuate interactions.
-
Random Tessellation Forests
O'ReillyElizaRandom forests are a popular class of algorithms used for regression and classification.
-
Back and forth between the beta distribution and edge stochastic domination in ERAPs
D'AchilleMatteoI will survey recent and less recent results on the phase diagram of Euclidean Random Assignment Problems (ERAPs)...
-
The unreasonable effectiveness of determinantal processes
GhoshSubhroshekharIn 1960, Wigner published an article famously titled “The Unreasonable Effectiveness of Mathematics in the Natural Sciences.
-
Structural properties of a conditioned random walk on the integer lattice with local constraints
FossSergueiWe consider a random walk on a one/multidimensional integer lattice with random bounds on local times, conditioned on the event that it hits a high level before its death.
-
Forward and backward limits
ThorissonHermannWe start by considering irreducible aperiodic positive recurrent Markov chains, and the proof of the main limit theorem...
-
-
Perfect simulation of interacting point processes with infinite interaction range
LöcherbachEvaI will present a (partly) new method for perfectly sampling from the stationary regime of point processes having an infinite number of interacting components.
Sur le même thème
-
Bruit, erreur, anomalie et incertitude dans les données-PUDD
RossiFabriceLes données collectées sont systématiquement soumises à des perturbations de diverses natures, depuis le bruit de mesure de capteurs jusqu’aux erreurs de saisie.
-
Combinatorial maps in high genus
LoufBaptisteCombinatorial maps are a model of discrete geometry: they are surfaces made by gluing polygons along their sides, or equivalently, graphs drawn on surfaces. In this talk, I'll focus on the study of
-
Do there exist expanders with non-negative curvature ?
SalezJustinIn this talk I will briefly recall the framework of local weak limits of finite graphs introduced by I. Benjamini and O. Schramm
-
Tail bounds for detection times in mobile hyperbolic graphs
MitscheDieterMotivated by Krioukov et al.'s model of random hyperbolic graphs for real-world networks, and inspired by the analysis of a dynamic model of graphs in Euclidean space by Peres et al., we introduce a
-
Sofic entropy of processes on infinite random trees
BordenaveCharlesThis is a joint work with Agnes Backhausz et Balasz Szegedy. We define a natural notion of micro-state entropy...
-
Online matching for the multiclass Stochastic Block Model
SOPRANO LOTONahuelA matching in a graph is a set of edges that do not share endpoints. Developing algorithms that find large matchings is an important problem. An algorithm is said to be online if it has to construct
-
Critical cluster cascades
KirchnerMatthiasWe consider a sequence of Poisson cluster point processes...
-
Point processes on higher rank symmetric spaces and their cost
MellickSamuelCost is a natural invariant associated to group actions and invariant point processes on symmetric spaces (such as Euclidean space and hyperbolic space). Informally, it measures how difficult it is to
-
Parallel server systems in extended heavy traffic
CastielEyalThe standard setting for studying parallel server systems (PSS) at the diffusion scale is based on the heavy traffic condition (HTC)...
-
The Maximal Agreement Subtree problem for random trees
BudzinskiThomasConsider two binary trees whose leaves are labelled from 1 to n.
-
An Improved Lower Bound on the Largest Common Subtree of Random Leaf-Labeled Binary Trees
KhezeliAliIt is known that the size of the largest common subtree...
-
Reversible Markov decision processes
AnantharamVenkatA Markov decision process is called reversible if for every stationary Markov control strategy the resulting Markov chain is reversible.