Notice
Petit jeu de physique sur un billard, réaction du support
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
Au centre d’un cercle d’environ 10cm de diamètre plaçons une bille de Billard sur laquelle en pose en équilibre une pièce de monnaie. Livrons nous maintenant à un petit jeu : Choquons la bille avec une autre bille et tentons de faire sortir la pièce du cercle. Facile me direz vous : un conseil ne pariez rien sur cette évidence car vous seriez souvent perdant même en changeant votre façon de choquer la bille. Imaginez donc une solution qui s’appuie sur un principe de physique : la réaction du support !!
Intervention
Thème
Documentation
Documents pédagogiques
Ce clip vidéo illustre l'une des 300 fiches constituant le site "Physique à main levée" basé sur des expériences de physique réalisables avec du matériel courant de la vie de tous les jours et engendrant une réflexion pédagogique sur les concepts physiques nécessaires à leur compréhension. Les domaines couverts en physique sont les suivants: mécanique, chaleur, acoustique, électricité, magnétisme, thermodynamique, etc…
Ces expériences illustrent les programmes de physique de L1, L2 avec des recoupements sur les programmes de 1ère et terminale; elles visent à redonner le goût de la physique aux étudiants grâce à des manipulations simples et démonstratives.
Chaque fiche présentée dans le site est ainsi
découpée: objectifs, illustration permettant de comprendre du premier
coup d'oeil de quoi il s'agit, liste des appareils et du matériel
nécessaire, description du montage, explications des notions physiques
intervenant dans l'expérience, conseils pédagogiques et méthode,
remarques, historique et/ou informations complémentaires, références
bibliographiques.
Consultez le site http://phymain.unisicel.fr
Dans la même collection
-
Une bobine qui remonte la pente
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Une bobine de magnétoscope sur laquelle il reste un bout de bande magnétique suffit pour réaliser cette expérience. Placée sur un plan incliné, la bobine contre toute attente reste immobile ; et
-
Période d'un pendule simple
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Cette expérience montre que la période d’oscillation d’un pendule simple ne dépend pas de la masse accrochée au fil, mais varie comme la racine carrée de sa longueur. http://phymain.unisciel.fr
-
Centre de gravité d'un balai
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
On montre ici comment trouver avec ses mains le centre de gravité d’un balai. http://phymain.unisciel.fr/centre-de-gravite-dun-balai/
-
La boîte qui remonte les pentes
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Un cylindre capable de remonter une pente montre que le moment du poids par rapport à la génératrice en contact avec la pente peut modifier le mouvement. http://phymain.unisciel.fr/la-boite-qui
-
Trajectoire d’une bille de billard, effets de l’effet
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Quand une bille de Billard est choquée autrement que sur son axe principal horizontal (passant par son centre), on dit qu’on l’anime d’un effet latéral. Cette bille de billard acquiert alors un
-
Pression avec un crayon
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Tout le monde sait qu'on peut se piquer un doigt avec la pointe d'un crayon bien taillé, mais beaucoup pensent que c'est parce que la force qui apparaît quand on appuie sur le crayon est plus
-
Rotation stable d'un stylo
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Un stylo est fixé au bout d’une ficelle tenue dans la main. Faisons-le tourner sur lui-même en décrivant des cercles avec la main. Lorsque la vitesse de rotation est suffisante, le stylo se met à
-
Le carton enchanté
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Un carton dont le centre d’inertie a été déplacé a un comportement surprenant. http://phymain.unisciel.fr/le-carton-enchante/
-
Choc entre 2 billes de billard par demi-bille, partage d’énergie et direction des billes
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Une bille (N°1) en choque une autre (N°2) par demi-bille. Que veut dire ce terme demi-bille ? Pour aider le joueur de Billard, pouvez- vous imaginer comment se partage l’énergie initialement
-
Pendule accroché à un ressort
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Deux boules d’acier accrochées par des fils à l’extrémité d’un ressort, claquent l’une sur l’autre à des intervalles réguliers lorsqu’on maintient leur point d’accrochage. Mais si on allonge le
-
Une bougie à bascule
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Une bougie mobile autour d’un axe horizontal et qui brûle par les deux bouts se met à basculer, illustrant ainsi l’influence de la position du centre de gravité dans le moment du poids. http:/
-
L'œuf culbuto
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Un œuf a été vidé puis partiellement rempli avec un peu de sable. Ainsi lesté, il se redresse toujours lorsqu’on essaie de le coucher sur la table.
Avec les mêmes intervenants et intervenantes
-
Le sablier amnésique
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Un sablier de cuisine, convenablement lesté, est plongé dans un récipient contenant de l’eau. Si on le place dans le récipient alors que tout le sable est en bas, le sablier coule immédiatement.
-
Tombera ? Tombera pas ?
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Voici cinq expériences prouvant que la position du centre de gravité d'une personne est primordiale pour assurer son équilibre. Toutes sont faciles à faire, mais attention : certaines ne sont pas
-
Le pendule de Galilée
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Un pendule de Galilée est un pendule simple dont on peut modifier la longueur grâce à une tige placée sur son parcours. La période est modifiée, mais le pendule s’immobilise à des hauteurs
-
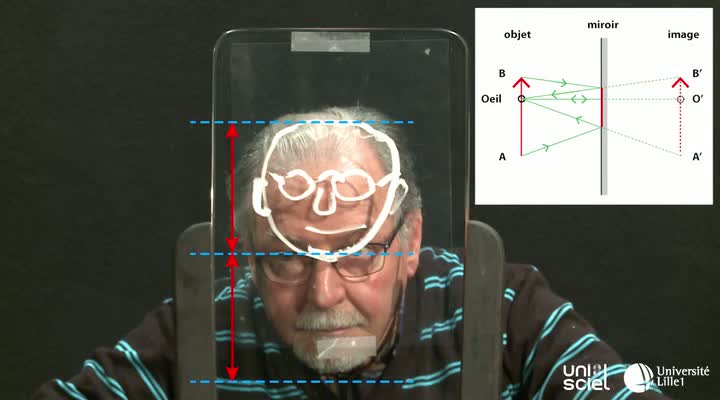
Le paradoxe des lentilles
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Une lentille à bords minces, convergente lorsqu’elle se trouve dans l’air, peut devenir divergente lorsqu’elle est plongée dans l’eau. Les propriétés d’une lentille ne dépendent donc pas
-
Une bulle d'air argentée
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Voici un dispositif très simple et que tout le monde peut fabriquer chez soi : un élastique coincé entre deux lames de verre ! Il permet pourtant d’illustrer de façon spectaculaire le phénomène de
-
Plus noir que noir
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Depuis un sketch dû à un humoriste maintenant disparu, « moins blanc que blanc » on sait ce que c’est. Mais « plus noir que noir » ? Mais si, ça existe aussi ! Venez voir. http://phymain.unisciel
-
Choc entre 2 billes de billard par demi-bille, partage d’énergie et direction des billes
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Une bille (N°1) en choque une autre (N°2) par demi-bille. Que veut dire ce terme demi-bille ? Pour aider le joueur de Billard, pouvez- vous imaginer comment se partage l’énergie initialement
-
Acrobaties autour du centre de gravité
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
On peut rendre stable un assemblage de divers objets en disposant astucieusement son centre de gravité. http://phymain.unisciel.fr/acrobaties-autour-du-centre-de-gravite/
-
Figures avec un bouton
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
On illustre que le moment cinétique est proportionnel au produit du moment d’inertie par la vitesse angulaire en faisant tourner un bouton sur un fil. http://phymain.unisciel.fr/figures-avec-un
-
Oscillations couplées de pinces à linge
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
On peut fabriquer des oscillateurs couplés avec deux pinces à linge et un élastique. http://phymain.unisciel.fr/oscillations-couplees-de-pinces-a-linge/
-
Comment courber un rayon lumineux ?
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
On peut visualiser les courants de convection au-dessus d’une flamme car l’indice de réfraction de l’air varie avec la température. http://phymain.unisciel.fr/comment-courber-un-rayon-lumineux/
-
Le faisceau lumineux captif
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Les lois de Snell-Descartes sur la réfraction sont ici illustrées avec un ballon sphérique éclairé par un rayon laser. Une barrette de plexiglas permet également de visualiser le phénomène de
Sur le même thème
-
Évaluation des courses : théorie
CHOLLET Didier
Sont abordés les aspects historiques, les données mesurées et la justification des paramètres utilisés, comme la vistesse, la fréquence, la distance par cycle et l'indice de nage.
-
Remédiation (capsule n°3) : L'oscillateur harmonique: équation du mouvment
CAPSULE n°3 (résumé) Pour la résolution de l’équation du mouvement de l’oscillateur harmonique M, nous admettons que les conditions initiales (position et vitesse à l'instant initial)
-
Remédiation (capsule n°4) : L'oscillateur harmonique: notion d'énergie mécanique
CAPSULE n°4 (résumé) Nous donnons une introduction heuristique à la notion d'énergie en essayant de montrer les difficultés de définition qui sont sous-jacentes. Nous définissons une énergie comme
-
Remédiation (capsule n°1) : L'oscillateur harmonique: du PFD à l'équation du mouvement
CAPSULE n°1 (résumé) Nous introduisons rapidement le principe fondamental de la dynamique : soit M un mobile de masse (inerte) m se déplaçant sur une droite et repéré par son abscisse q(t)
-
Remédiation (capsule n°5) : L'oscillateur harmonique: conservation de l'énergie mécanique
CAPSULE n°5 (résumé) Nous vérifions la loi de conservation de l'énergie mécanique pour l'oscillateur harmonique de deux manières différentes.
-
Remédiation (capsule n°2) : L'oscillateur harmonique: notion de dimension, homogénéité des formules
CAPSULE n°2 Afin d’obtenir une interprétation physique de la pulsation nous introduisons des notions sur le calcul des dimensions physiques et nous abordons la question de l’homogénéité des
-
Remédiation (capsule n°6) : L'oscillateur harmonique: exercice sur le rapport entre deux fréquences…
CAPSULE n°6 (résumé) Nous proposons une présentation et une résolution complète d'un exercice sur l'oscillateur harmonique. A partir de deux mesures f_1 et f_2 de la fréquence d'un oscillateur
-
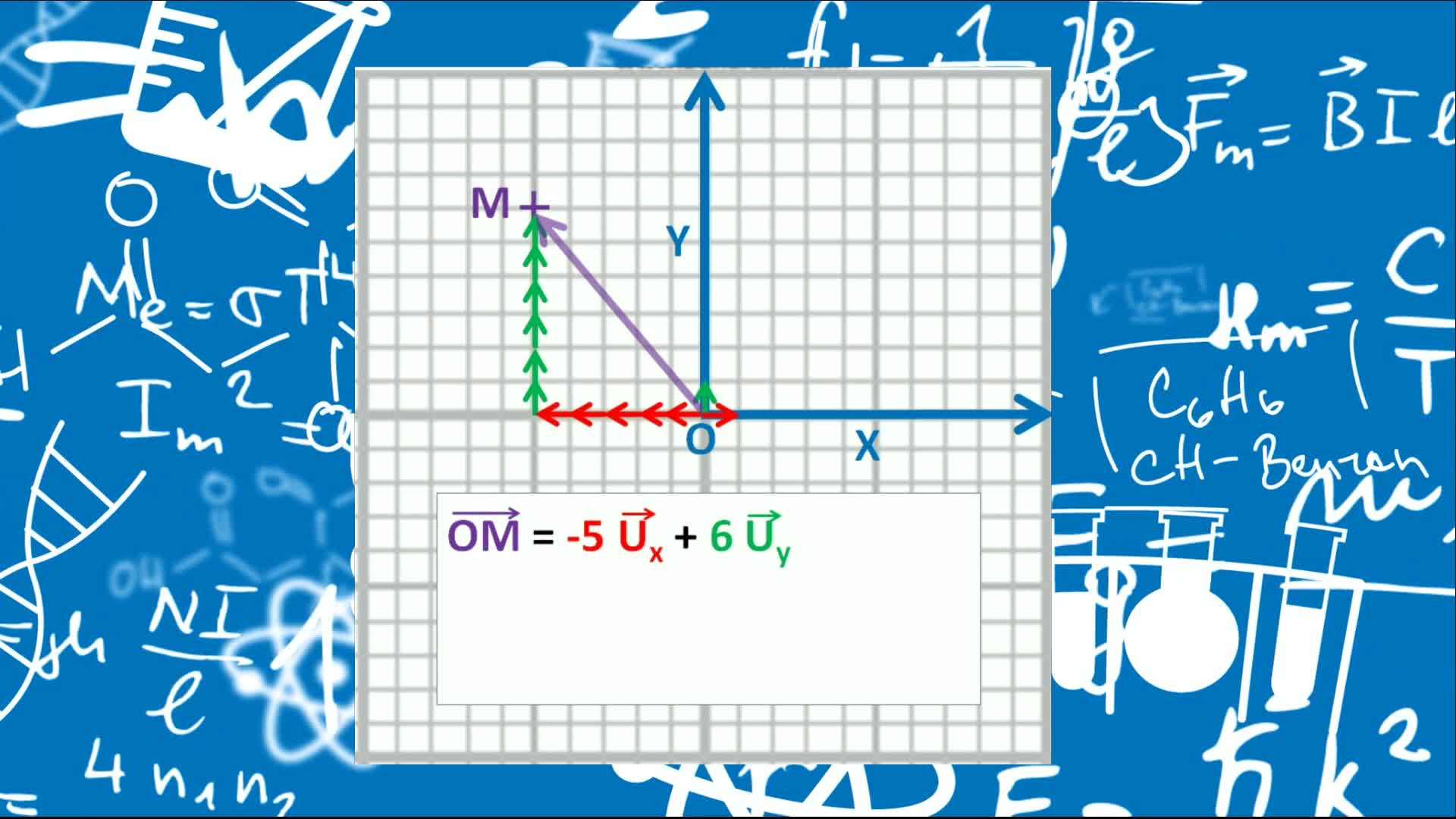
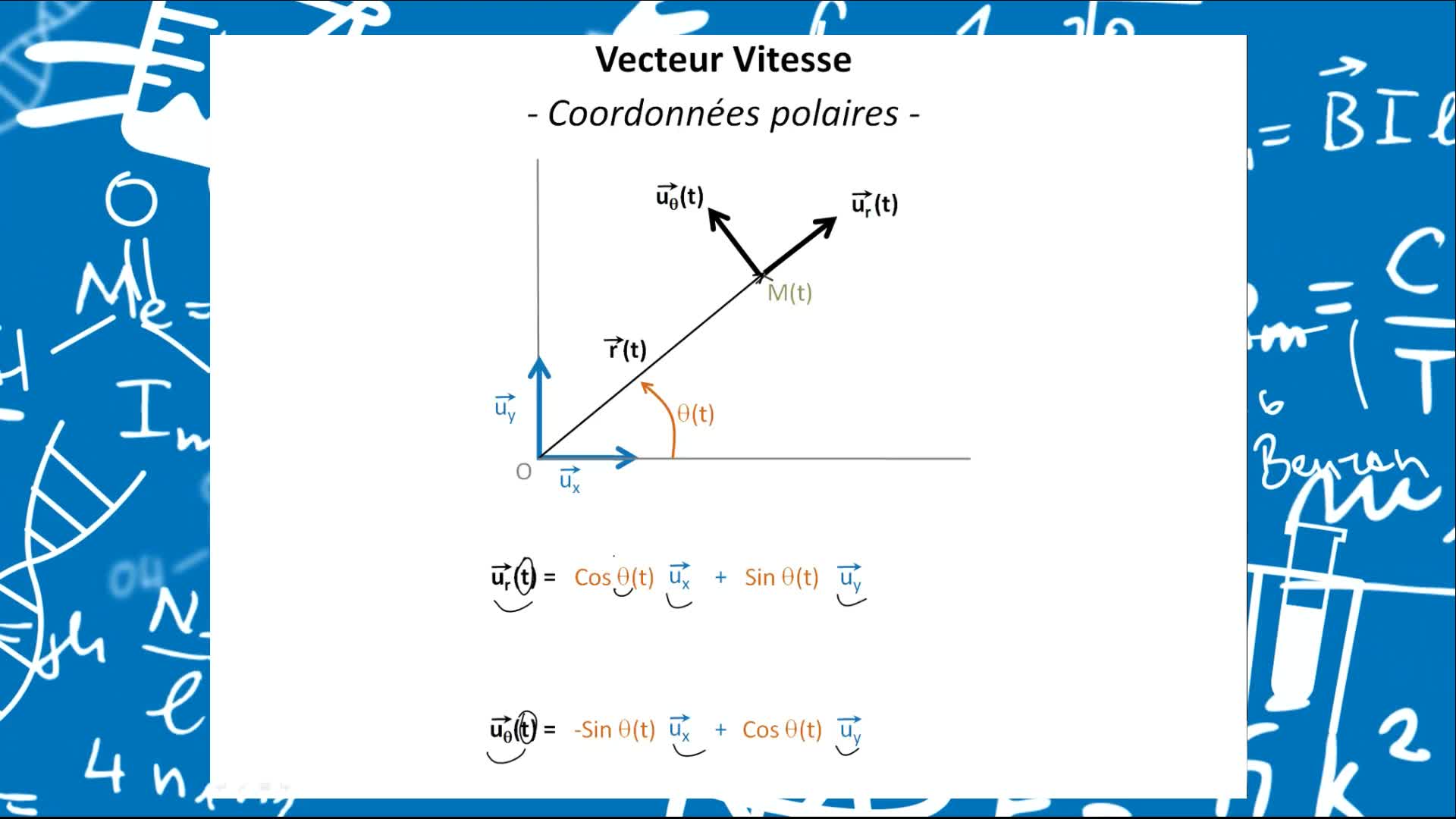
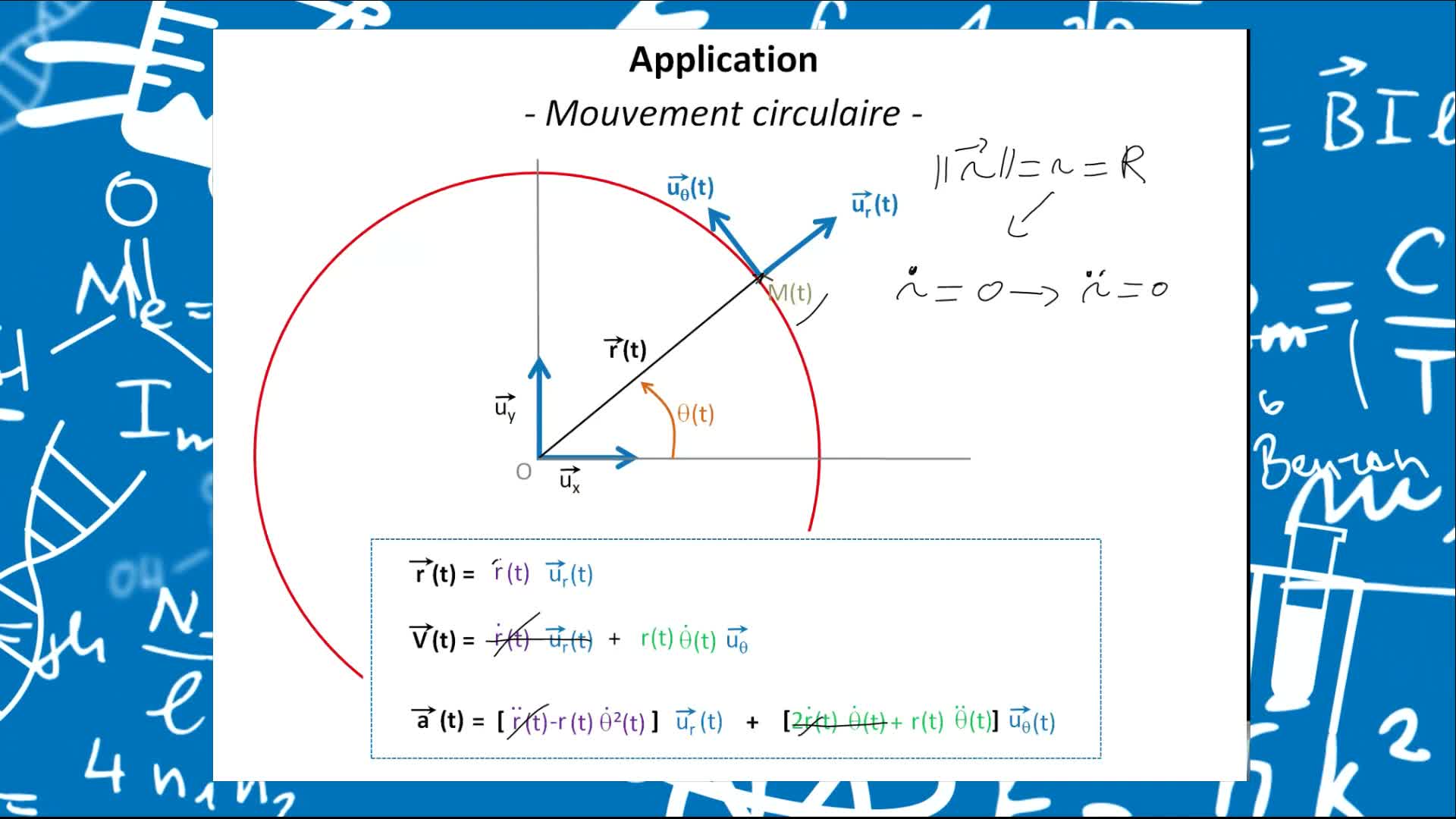
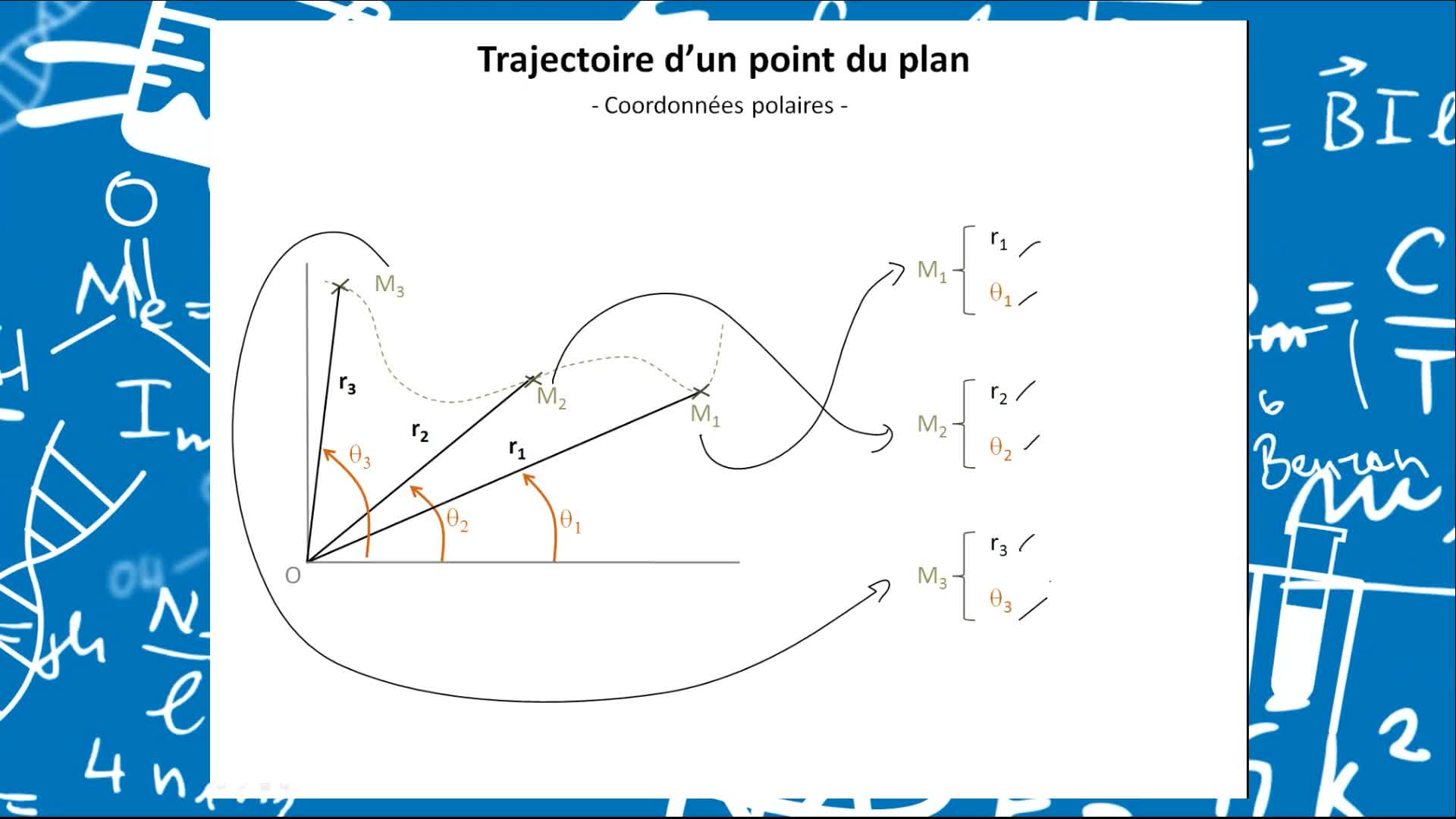
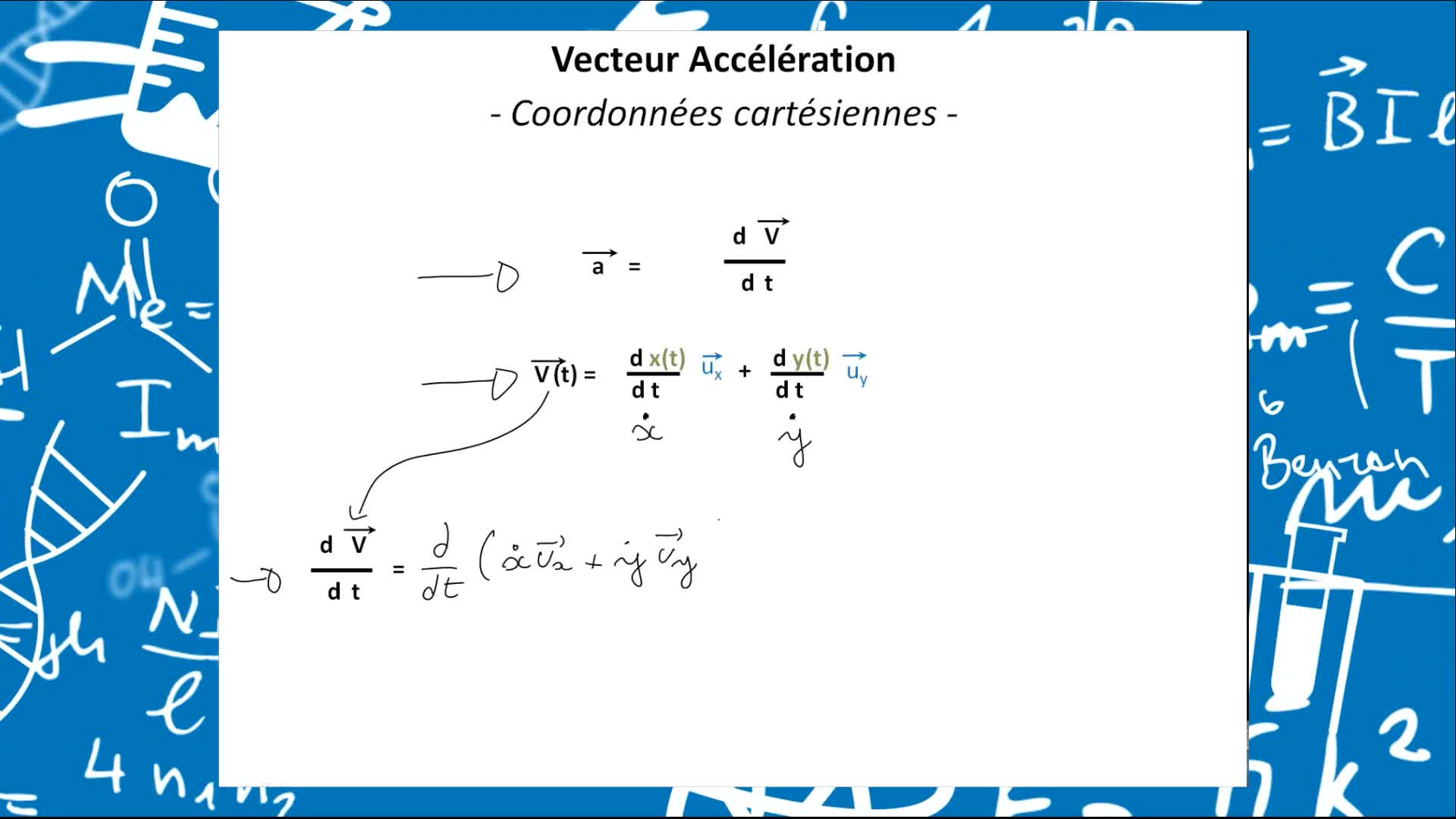
Remediation - Vecteurs position, vitesses et accélérations décrits en coordonnées cartésiennes et p…
PARDANAUD Cédric
L'objectif premier de cet élément de remédiation est de faire prendre conscience que les vecteurs vitesses et accélérations sont bien des vecteurs, et que cela n'est pas sans conséquences sur la
-
Remediation - Vecteurs position, vitesses et accélérations décrits en coordonnées cartésiennes et p…
PARDANAUD Cédric
L'objectif premier de cet élément de remédiation est de faire prendre conscience que les vecteurs vitesses et accélérations sont bien des vecteurs, et que cela n'est pas sans conséquences sur la
-
Remediation - Vecteurs position, vitesses et accélérations décrits en coordonnées cartésiennes et p…
PARDANAUD Cédric
L'objectif premier de cet élément de remédiation est de faire prendre conscience que les vecteurs vitesses et accélérations sont bien des vecteurs, et que cela n'est pas sans conséquences sur la
-
Remediation - Vecteurs position, vitesses et accélérations décrits en coordonnées cartésiennes et p…
PARDANAUD Cédric
L'objectif premier de cet élément de remédiation est de faire prendre conscience que les vecteurs vitesses et accélérations sont bien des vecteurs, et que cela n'est pas sans conséquences sur la
-
Remediation - Vecteurs position, vitesses et accélérations décrits en coordonnées cartésiennes et p…
PARDANAUD Cédric
L'objectif premier de cet élément de remédiation est de faire prendre conscience que les vecteurs vitesses et accélérations sont bien des vecteurs, et que cela n'est pas sans conséquences sur la
