Notice
Sur quelle trajectoire le mouvement est-il le plus rapide ? (Expérience du brachistochrone)
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
Cette expérience contredit l'idée reçue que le chemin le plus rapide pour aller d'un point à un autre est forcément la ligne droite qui joint ces deux points. Deux billes identiques partent d'un même point A pour arriver au même point B, mais en suivant deux trajectoires d'inégale longueur. Sauriez-vous prévoir quelle est celle qui arrivera la première ?
Intervention
Thème
Documentation
Documents pédagogiques
Ce clip vidéo illustre l'une des 300 fiches constituant le site "Physique à main levée" basé sur des expériences de physique réalisables avec du matériel courant de la vie de tous les jours et engendrant une réflexion pédagogique sur les concepts physiques nécessaires à leur compréhension. Les domaines couverts en physique sont les suivants: mécanique, chaleur, acoustique, électricité, magnétisme, thermodynamique, etc…
Ces expériences illustrent les programmes de physique de L1, L2 avec des recoupements sur les programmes de 1ère et terminale; elles visent à redonner le goût de la physique aux étudiants grâce à des manipulations simples et démonstratives.
Chaque fiche présentée dans le site est ainsi
découpée: objectifs, illustration permettant de comprendre du premier
coup d'oeil de quoi il s'agit, liste des appareils et du matériel
nécessaire, description du montage, explications des notions physiques
intervenant dans l'expérience, conseils pédagogiques et méthode,
remarques, historique et/ou informations complémentaires, références
bibliographiques.
Consultez le site http://phymain.unisicel.fr
Dans la même collection
-
Choc frontal entre 2 billes de billard, partage des énergies et direction des billes
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Carreau, Coulé, Rétro : 3 termes utilisés couramment par le joueur de Billard. Mais au fait comment réalise-t-on ces 3 coups ? Imaginez 2 billes qui se choquent « en plein ». Pouvez- vous imaginer
-
Le pendule de Galilée
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Un pendule de Galilée est un pendule simple dont on peut modifier la longueur grâce à une tige placée sur son parcours. La période est modifiée, mais le pendule s’immobilise à des hauteurs
-
Tombera ? Tombera pas ?
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Voici cinq expériences prouvant que la position du centre de gravité d'une personne est primordiale pour assurer son équilibre. Toutes sont faciles à faire, mais attention : certaines ne sont pas
-
Le sablier amnésique
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Un sablier de cuisine, convenablement lesté, est plongé dans un récipient contenant de l’eau. Si on le place dans le récipient alors que tout le sable est en bas, le sablier coule immédiatement.
-
Petit jeu de physique sur un billard, réaction du support
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Au centre d’un cercle d’environ 10cm de diamètre plaçons une bille de Billard sur laquelle en pose en équilibre une pièce de monnaie. Livrons nous maintenant à un petit jeu : Choquons la bille
-
Un ballon increvable
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Un ballon de baudruche piqué d’un trou d’épingle n’explose pas si l’on a pris la peine de le « préparer » avec un morceau de ruban adhésif. http://phymain.unisciel.fr/un-ballon-increvable/
-
Pile ou face ?
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
On utilise des pièces pour montrer la « loi de Murphy » ou « loi de la tartine beurrée ». http://phymain.unisciel.fr/pile-ou-face/
-
Un manège avec une assiette
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Un assemblage constitué d’une assiette, deux bouchons et quatre fourchettes est placé en équilibre stable sur la pointe d’une aiguille. http://phymain.unisciel.fr/un-manege-avec-une-assiette/
-
Choc entre 2 billes de billard par finesse, partage d’énergie et direction des billes
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Une bille (N°1) en choque une autre (N°2) par « finesse ». Que veut dire ce terme « finesse » ? Pour aider le joueur de Billard, pouvez- vous imaginer comment se partage l’énergie initialement
-
Un pendule de longueur variable (2)
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Voici une expérience très simple pour montrer que la période d’oscillation d’un pendule dépend de sa longueur. Le fil du pendule est passé sur un doigt de l’opérateur, et de l’autre main celui-ci
-
Quelle tige tombe le plus vite ?
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Des tiges sur lesquelles les masses sont réparties différemment ne tombent pas de la même façon. Ceci permet de montrer comment le moment de la force exercée et le moment d’inertie dépendent de la
-
Un chef d'œuvre d'équilibre
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
On peut disposer sur un verre un assemblage de deux fourchettes et d’une pièce de monnaie de façon à créer un équilibre stable. http://phymain.unisciel.fr/loeuf-culbuto/
Avec les mêmes intervenants et intervenantes
-
Le carton enchanté
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Un carton dont le centre d’inertie a été déplacé a un comportement surprenant. http://phymain.unisciel.fr/le-carton-enchante/
-
Rotation stable d'un stylo
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Un stylo est fixé au bout d’une ficelle tenue dans la main. Faisons-le tourner sur lui-même en décrivant des cercles avec la main. Lorsque la vitesse de rotation est suffisante, le stylo se met à
-
Pression avec un crayon
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Tout le monde sait qu'on peut se piquer un doigt avec la pointe d'un crayon bien taillé, mais beaucoup pensent que c'est parce que la force qui apparaît quand on appuie sur le crayon est plus
-
Images par réflexion sur une cuillère
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Qui aurait cru qu’une simple cuillère à café peut servir à illustrer les propriétés des miroirs sphériques ? Voici une expérience très instructive, et qui demande peu de matériel. http://phymain
-
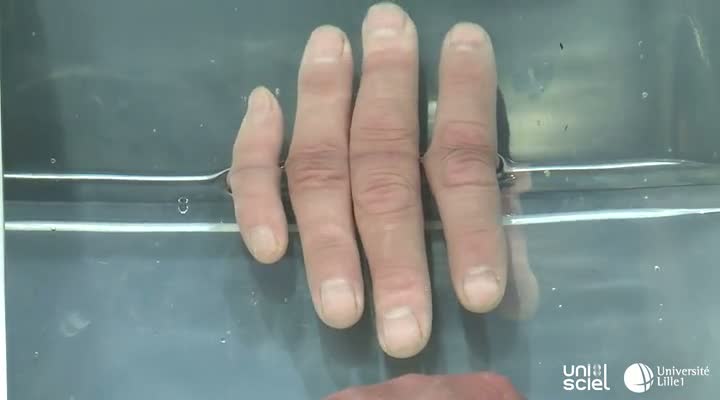
Les doigts doubles
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Réalisée avec une cuve à eau et un simple miroir, voici une expérience étonnante qui semble multiplier par deux les doigts d’une main. Une application originale et ludique du phénomène de
-
Le nez de Pinocchio
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
L'ombre du nez d'un personnage éclairé par une puissante lampe semble s'allonger lorsqu'on approche une feuille de papier dans le faisceau lumineux. Avec cette expérience spectaculaire, tout le
-
Petit jeu de physique sur un billard, réaction du support
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Au centre d’un cercle d’environ 10cm de diamètre plaçons une bille de Billard sur laquelle en pose en équilibre une pièce de monnaie. Livrons nous maintenant à un petit jeu : Choquons la bille
-
La boîte qui remonte les pentes
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Un cylindre capable de remonter une pente montre que le moment du poids par rapport à la génératrice en contact avec la pente peut modifier le mouvement. http://phymain.unisciel.fr/la-boite-qui
-
Centre de gravité d'un balai
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
On montre ici comment trouver avec ses mains le centre de gravité d’un balai. http://phymain.unisciel.fr/centre-de-gravite-dun-balai/
-
Période d'un pendule simple
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Cette expérience montre que la période d’oscillation d’un pendule simple ne dépend pas de la masse accrochée au fil, mais varie comme la racine carrée de sa longueur. http://phymain.unisciel.fr
-
La baguette qui disparaît derrière un verre d’eau
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Une baguette de bois passée derrière un verre ou tout récipient cylindrique n'apparaît que si elle est placée près de l'axe du récipient. Si on l'approche des parois latérales, elle n'est plus
-
Réflexion sur deux miroirs plans
BLONDEAU Jean-Marie
BONNEL Bernard
MIKOLAJCZAK Bernard
DESTRUN Gérard
Cette vidéo montre les propriétés optiques de deux, puis trois miroirs plans perpendiculaires. Avec trois miroirs, tout rayon revient vers la source en restant rigoureusement parallèle au rayon
Sur le même thème
-
Évaluation des courses : théorie
CHOLLET Didier
Sont abordés les aspects historiques, les données mesurées et la justification des paramètres utilisés, comme la vistesse, la fréquence, la distance par cycle et l'indice de nage.
-
Remédiation (capsule n°3) : L'oscillateur harmonique: équation du mouvment
CAPSULE n°3 (résumé) Pour la résolution de l’équation du mouvement de l’oscillateur harmonique M, nous admettons que les conditions initiales (position et vitesse à l'instant initial)
-
Remédiation (capsule n°4) : L'oscillateur harmonique: notion d'énergie mécanique
CAPSULE n°4 (résumé) Nous donnons une introduction heuristique à la notion d'énergie en essayant de montrer les difficultés de définition qui sont sous-jacentes. Nous définissons une énergie comme
-
Remédiation (capsule n°1) : L'oscillateur harmonique: du PFD à l'équation du mouvement
CAPSULE n°1 (résumé) Nous introduisons rapidement le principe fondamental de la dynamique : soit M un mobile de masse (inerte) m se déplaçant sur une droite et repéré par son abscisse q(t)
-
Remédiation (capsule n°5) : L'oscillateur harmonique: conservation de l'énergie mécanique
CAPSULE n°5 (résumé) Nous vérifions la loi de conservation de l'énergie mécanique pour l'oscillateur harmonique de deux manières différentes.
-
Remédiation (capsule n°2) : L'oscillateur harmonique: notion de dimension, homogénéité des formules
CAPSULE n°2 Afin d’obtenir une interprétation physique de la pulsation nous introduisons des notions sur le calcul des dimensions physiques et nous abordons la question de l’homogénéité des
-
Remédiation (capsule n°6) : L'oscillateur harmonique: exercice sur le rapport entre deux fréquences…
CAPSULE n°6 (résumé) Nous proposons une présentation et une résolution complète d'un exercice sur l'oscillateur harmonique. A partir de deux mesures f_1 et f_2 de la fréquence d'un oscillateur
-
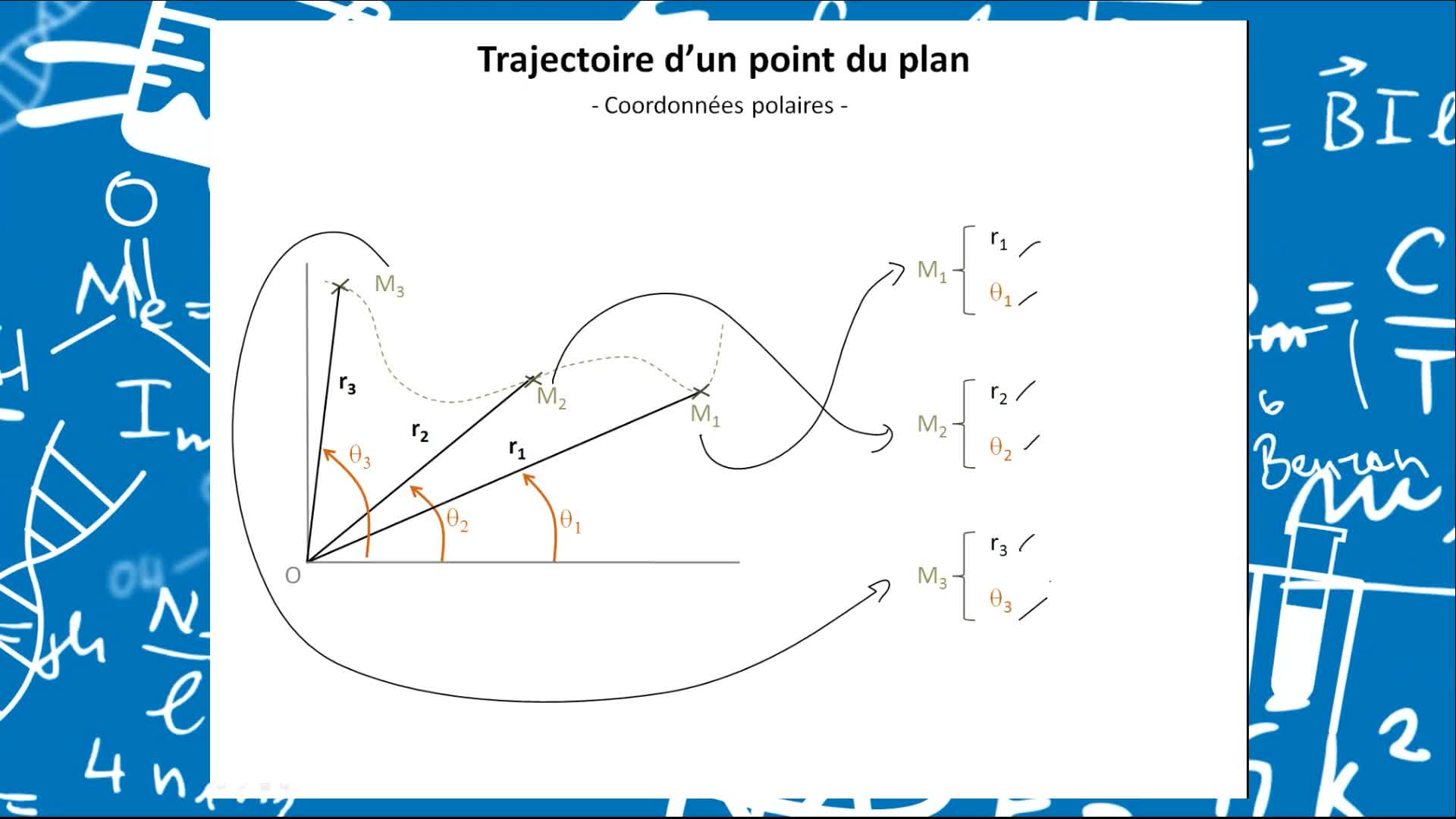
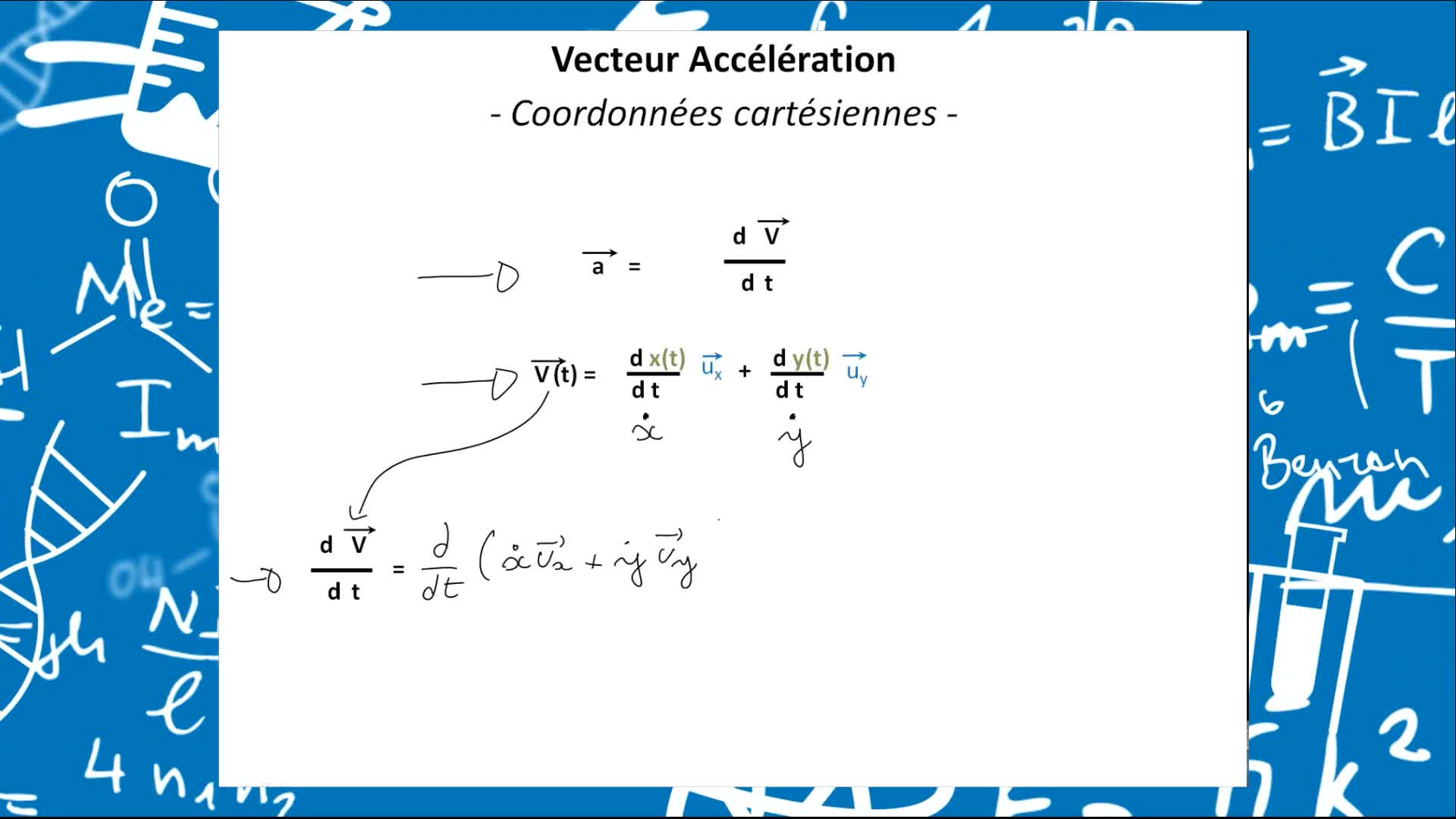
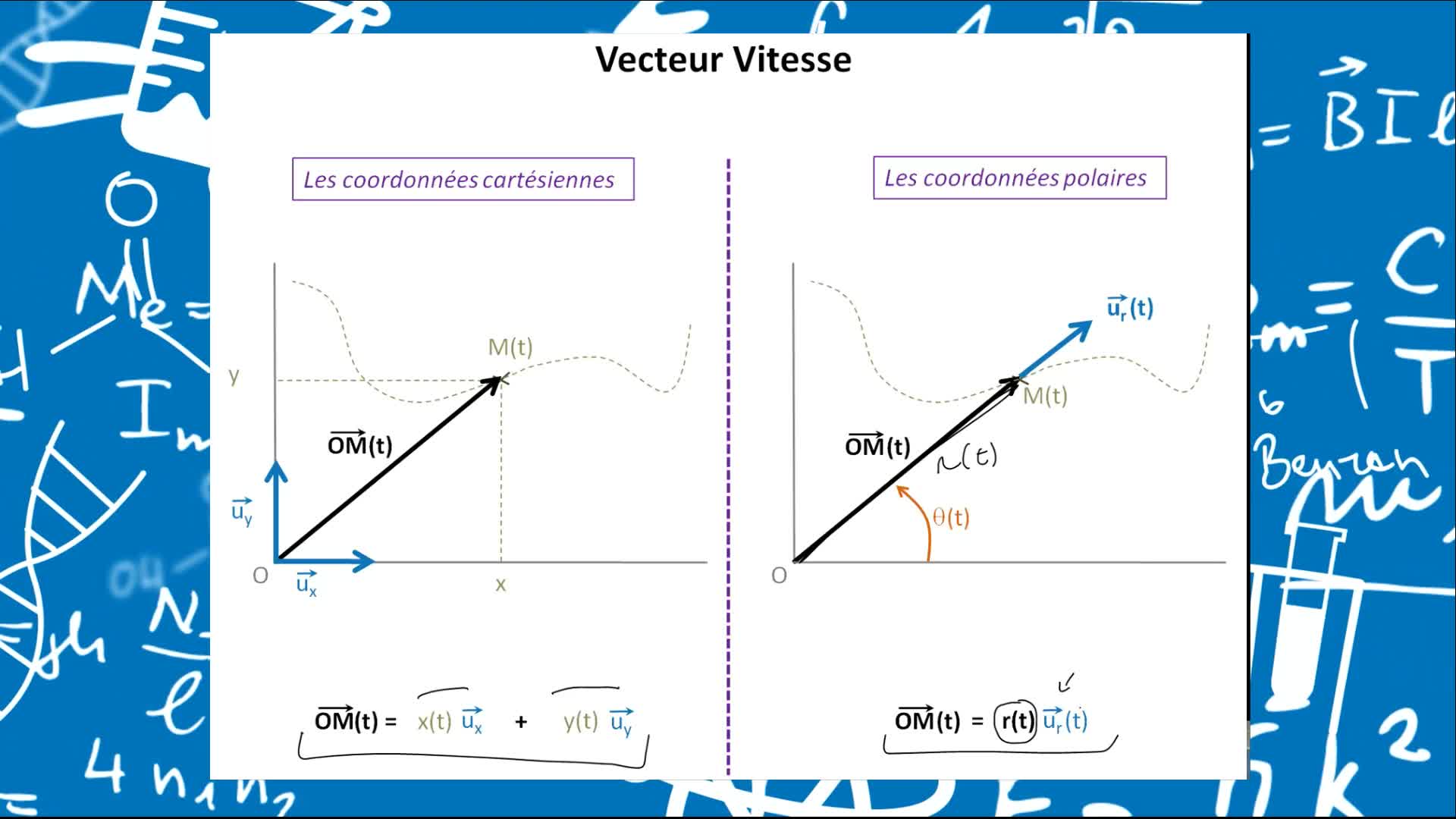
Remediation - Vecteurs position, vitesses et accélérations décrits en coordonnées cartésiennes et p…
PARDANAUD Cédric
L'objectif premier de cet élément de remédiation est de faire prendre conscience que les vecteurs vitesses et accélérations sont bien des vecteurs, et que cela n'est pas sans conséquences sur la
-
Remediation - Vecteurs position, vitesses et accélérations décrits en coordonnées cartésiennes et p…
PARDANAUD Cédric
L'objectif premier de cet élément de remédiation est de faire prendre conscience que les vecteurs vitesses et accélérations sont bien des vecteurs, et que cela n'est pas sans conséquences sur la
-
Remediation - Vecteurs position, vitesses et accélérations décrits en coordonnées cartésiennes et p…
PARDANAUD Cédric
L'objectif premier de cet élément de remédiation est de faire prendre conscience que les vecteurs vitesses et accélérations sont bien des vecteurs, et que cela n'est pas sans conséquences sur la
-
Remediation - Vecteurs position, vitesses et accélérations décrits en coordonnées cartésiennes et p…
PARDANAUD Cédric
L'objectif premier de cet élément de remédiation est de faire prendre conscience que les vecteurs vitesses et accélérations sont bien des vecteurs, et que cela n'est pas sans conséquences sur la
-
Remediation - Vecteurs position, vitesses et accélérations décrits en coordonnées cartésiennes et p…
PARDANAUD Cédric
L'objectif premier de cet élément de remédiation est de faire prendre conscience que les vecteurs vitesses et accélérations sont bien des vecteurs, et que cela n'est pas sans conséquences sur la
