Notice
Enigma, ou comment les mathématiciens ont gagné la guerre 1939-45. (Partie 3)
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
Dans cet exposé, à la fois historique et technique, nous expliquerons
tout d'abord comment les machines à chiffrer Enigma ont pu être
cryptanalysées durant la deuxième guerre mondiale. Nous nous
efforcerons ensuite de dégager les grands principes qui sont à
l'oeuvre aussi bien dans l'analyse des machines à rotors historiques
que dans le chiffrement par blocs moderne. Dans les deux cas il
s'agit de constructions à base de combinaisons (non-commutatives!) de
permutations et il existe un certain nombre de stratégies qui
permettent de déjouer leur apparente complexité. Nous expliquerons le
rôle majeur joué par certaines propriétés et théorèmes clés sur les
permutations, qui concernent, notamment, les involutions, les cycles
courts et les points fixes.
Intervention / Responsable scientifique
Avec les mêmes intervenants et intervenantes
-
Enigma, ou comment les mathématiciens ont gagné la guerre 1939-45. (Partie 5)
CourtoisNicolas T.Dans cet exposé, à la fois historique et technique, nous expliquerons tout d'abord comment les machines à chiffrer Enigma ont pu être cryptanalysées durant la deuxième guerre mondiale. Nous nous
-
Enigma, ou comment les mathématiciens ont gagné la guerre 1939-45. (Partie 1)
CourtoisNicolas T.Dans cet exposé, à la fois historique et technique, nous expliquerons tout d'abord comment les machines à chiffrer Enigma ont pu être cryptanalysées durant la deuxième guerre mondiale. Nous nous
-
Enigma, ou comment les mathématiciens ont gagné la guerre 1939-45. (Partie 4)
CourtoisNicolas T.Dans cet exposé, à la fois historique et technique, nous expliquerons tout d'abord comment les machines à chiffrer Enigma ont pu être cryptanalysées durant la deuxième guerre mondiale. Nous nous
Sur le même thème
-
Quand la BD reveille l'Antiquité
LonniMarieGallegoJulieDans ce neuvième épisode, Marie Lonni a pu échanger avec Julie Gallego.
-
Les transformations contemporaines des cabanes de pêcheurs de l'île Sainte-Marguerite.
Rosati-MarzettiChloéProjet soutenu par la MSHS Sud-Est, il émane plus particulièrement de l’axe 1 du LAPCOS « Territoires et environnements : approches plurivoques de l'habiter ». Dans le cadre de l'axe 4 de la MSHS Sud
-
Quel est le prix à payer pour la sécurité de nos données ?
MinaudBriceÀ l'ère du tout connecté, la question de la sécurité de nos données personnelles est devenue primordiale. Comment faire pour garder le contrôle de nos données ? Comment déjouer les pièges de plus en
-
Des systèmes de numération pour le calcul modulaire
BajardJean-ClaudeLe calcul modulaire est utilisé dans de nombreuses applications des mathématiques...
-
Inauguration de l'exposition - Vanessa Vitse : Nombres de Sophie Germain et codes secrets
VitseVanessaExposé de Vanessa Vitse (Institut Fourier) : Nombres de Sophie Germain et codes secrets
-
Interview d'Aleksandr Musin dans le cadre du Programme PAUSE
MusinAleksandr EvgenʹevičLe CRAHAM accueille depuis le début du mois de mars 2023 Aleksandr Musin, dans le cadre d'un programme d’accueil de chercheurs en exil piloté par le Collège de France. A. Musin présentera ses
-
-
Usages et interprétations du dessin d’enfant en histoire (Manon Pignot)
PignotManonUsages et interprétations du dessin d’enfant en histoire (Manon Pignot)
-
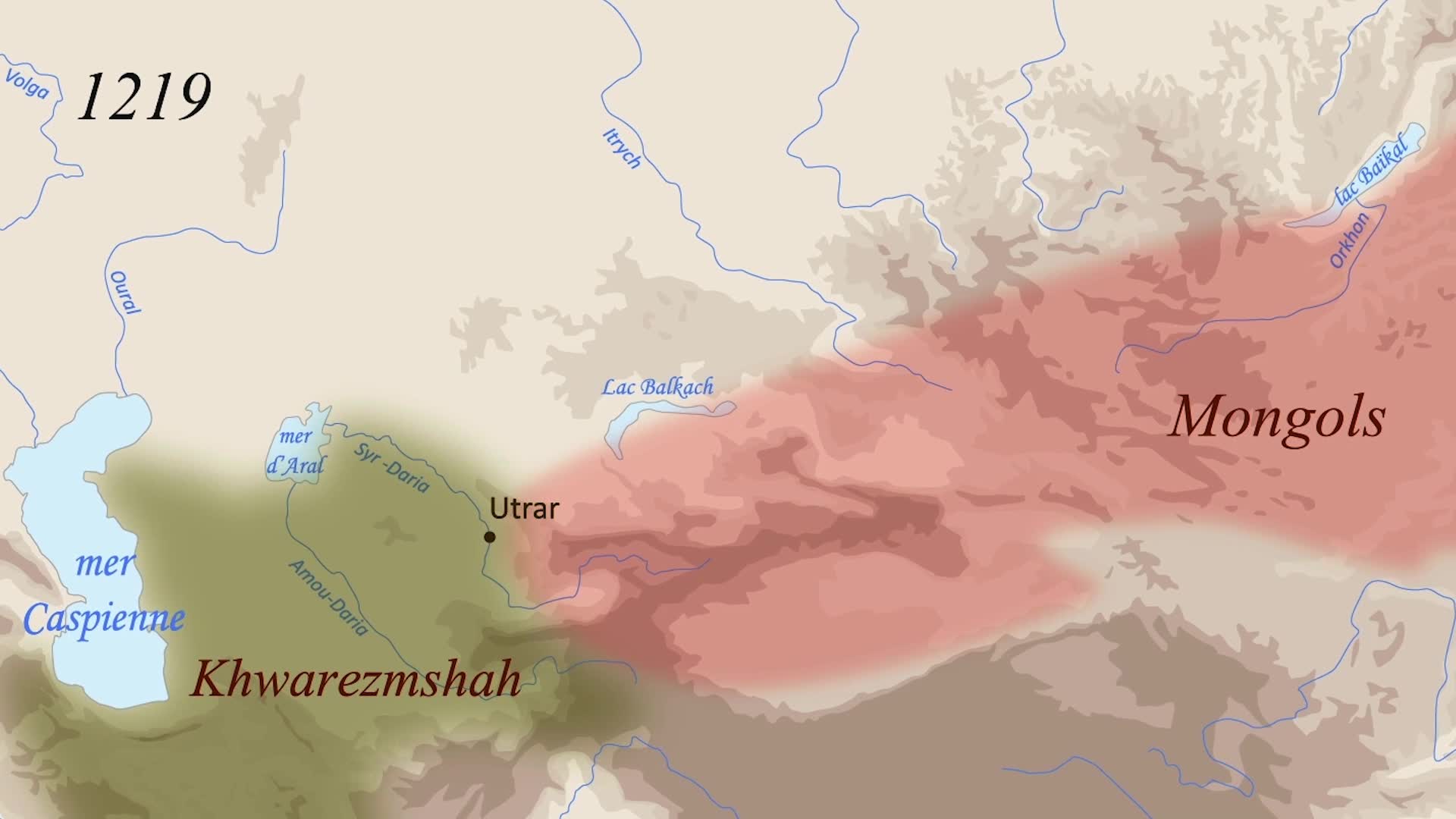
Empire mongol 3/3 : les campagnes de Gengis Khan (1206-1227)
FavereauMarieLa construction de l'empire mongol du XIIIe siècle reliant la Chine à l'Europe sous l'égide de Gengis Khan. Cette vidéo développe un des thèmes abordé dans l'ouvrage "Atlas des mondes musulmans
-
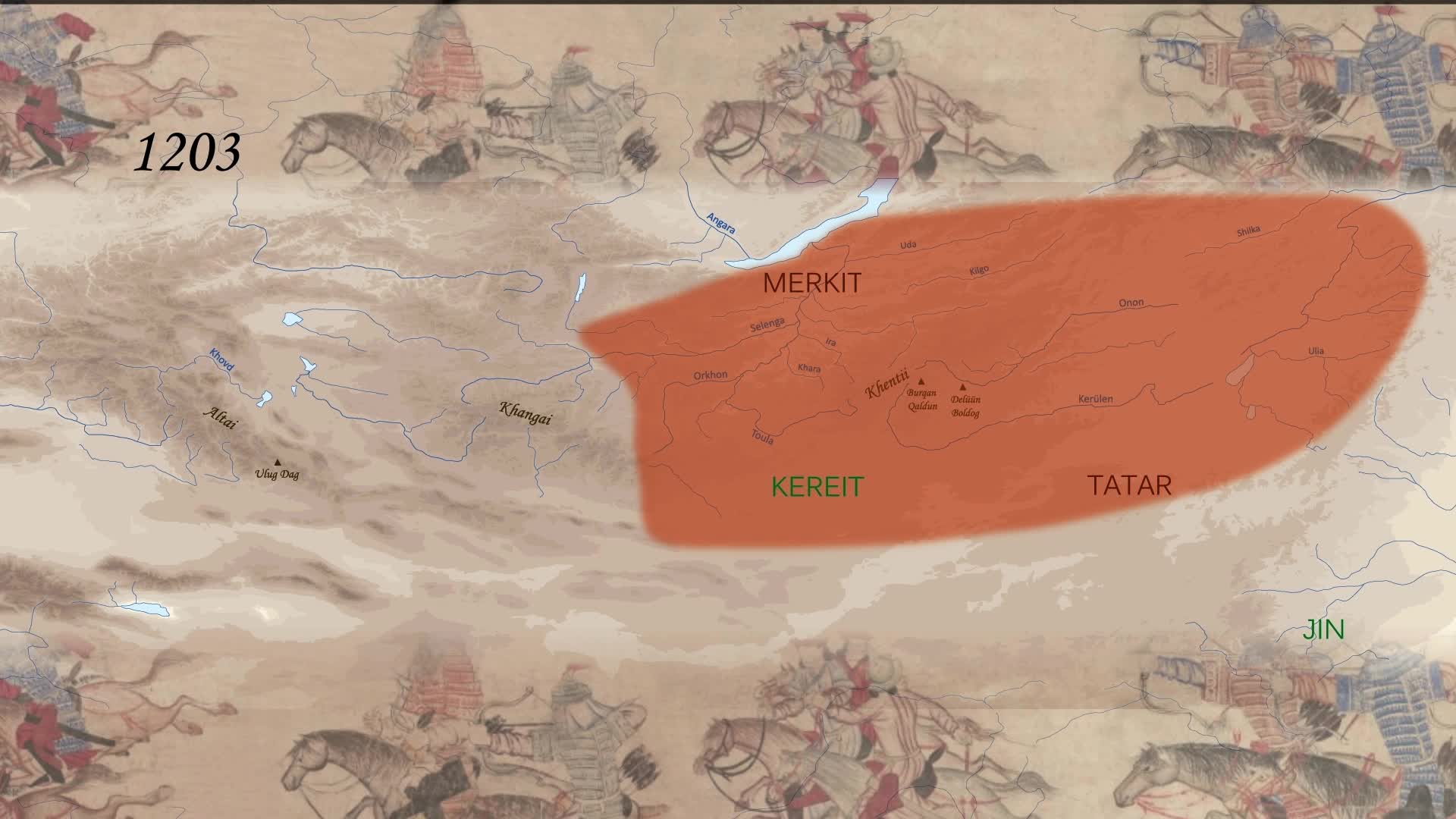
Empire mongol 2/3 : l'unification des nomades de la steppe
FavereauMarieL'histoire de l'unification des tribus mongols de la grande steppe par Gengis Khan. Prémices de l'empire mongol du XIIIe siècle. Cette vidéo développe un des thèmes abordé dans l'ouvrage "Atlas des
-
Empire mongol 1/3 : la grande steppe
FavereauMarieVidéo présentant la grande steppe berceau de l'Empire mongol. Elle approfondit un des thèmes abordé dans l'ouvrage "Atlas des mondes musulmans médiévaux" , Denoix, S. et Renel H. (éds.), Paris, Cnrs
-
Séminaire HN Lab 1 : Le HTR appliqué à l’histoire de l’Art : présentation du travail de Léa Marone…
Le HN Lab propose un séminaire de recherche qui prend la forme d’une présentation de problématiques théoriques ou pratiques, de présentations de réalisations (achevées ou en cours) d’une durée de 30