Notice
Des systèmes de numération pour le calcul modulaire
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
Le calcul modulaire est utilisé dans de nombreuses applications des mathématiques, telles que la cryptographie. La réduction modulaire dans un contexte très général est coûteuse, car elle nécessite principalement une division. Dans la pratique, cependant, le modulo est souvent fi xe, par exemple lorsqu’on calcule sur un corps fi ni, et il est donc possible de mettre en oeuvre des stratégies pour réduire le coût de la réduction. Les premières approches consistent, si l’on a le choix, à travailler avec des modulo particuliers, comme les nombres premiers de Mersenne ou les pseudo-premiers de Mersenne, voire des généralisations de ces formes. D’autres approches consistent à faire des réductions modulaires sans division avec des modules qui n’ont pas de particularités, comme les algorithmes de Montgomery ou de Barrett. Un autre type de stratégies revient à travailler sur les systèmes de numération pour améliorer le calcul ou la réduction.
C’est le cas des systèmes de nombres résiduels basés sur le théorème du reste chinois, où le gain se fait sur la multiplication et l’addition, et avec lesquels la réduction de Montgomery est adaptable. Nous pouvons également construire des systèmes modulo-dépendants qui prennent une forme similaire à celle du pseudo-Mersenne. Les réductions ici sont similaires à la recherche du vecteur le plus proche dans un réseau euclidien. Enfi n, le produit modulaire peut être considéré comme un changement de représentation vers une base d’Ostrowski sur les entiers.
Thème
Sur le même thème
-
Quel est le prix à payer pour la sécurité de nos données ?
MinaudBriceÀ l'ère du tout connecté, la question de la sécurité de nos données personnelles est devenue primordiale. Comment faire pour garder le contrôle de nos données ? Comment déjouer les pièges de plus en
-
Inauguration de l'exposition - Vanessa Vitse : Nombres de Sophie Germain et codes secrets
VitseVanessaExposé de Vanessa Vitse (Institut Fourier) : Nombres de Sophie Germain et codes secrets
-
Information Structures for Privacy and Fairness
PalamidessiCatusciaInformation Structures for Privacy and Fairness
-
AI and Human Decision-Making: An Interdisciplinary Perspective
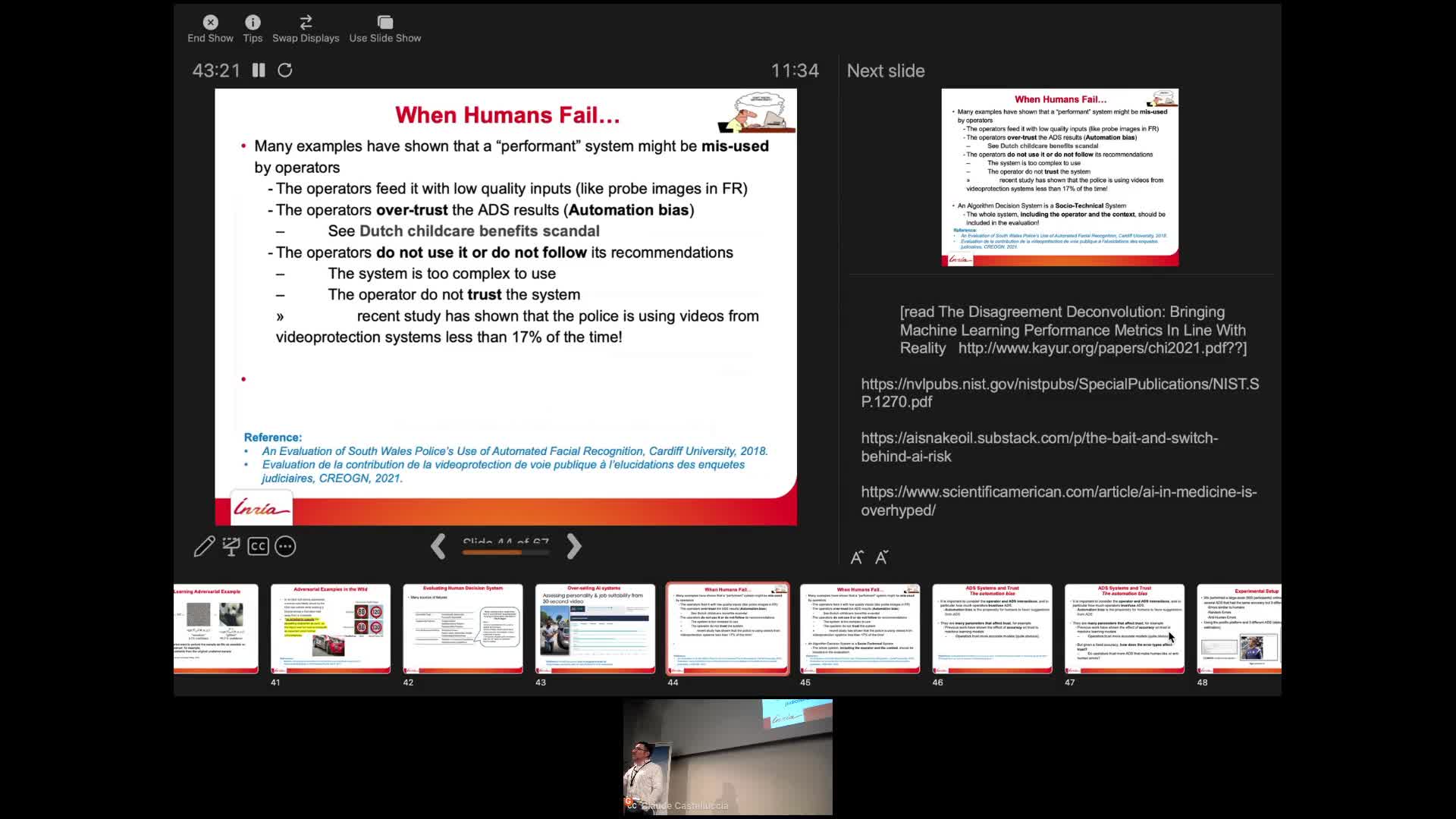
CastellucciaClaudeThis seminar will talk about some of the privacy risks of these systems and will describe some recent attacks. It will also discuss why they sometimes fail to deliver. Finally, we will also show that
-
4.5. Error-Correcting Pairs
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuWe present in this session a general decoding method for linear codes. And we will see it in an example. Let C be a generalized Reed-Solomon code of dimension k associated to the pair (c, d). Then,
-
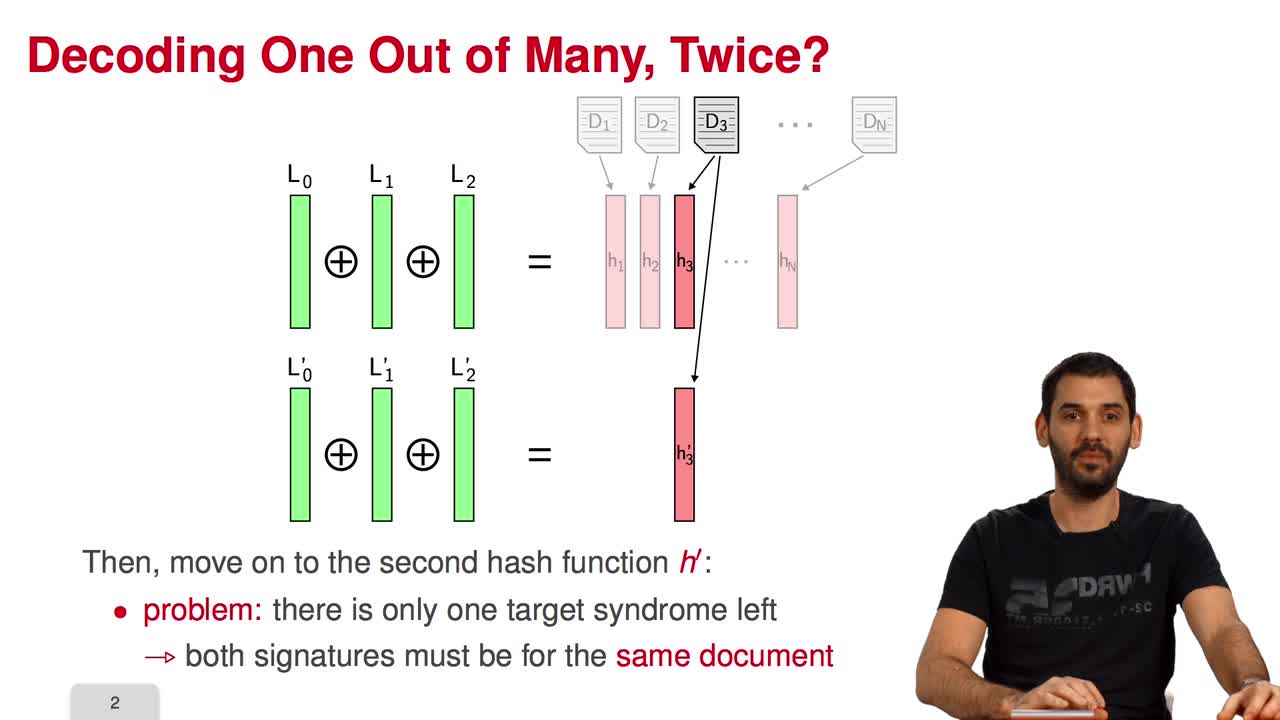
5.4. Parallel-CFS
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session, I will present a variant of the CFS signature scheme called parallel-CFS. We start from a simple question: what happens if you try to use two different hash functions and compute
-
4.8. Attack against Algebraic Geometry codes
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session, we will present an attack against Algebraic Geometry codes (AG codes). Algebraic Geometry codes is determined by a triple. First of all, an algebraic curve of genus g, then a n
-
5.7. The Fast Syndrome-Based (FSB) Hash Function
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn the last session of this week, we will have a look at the FSB Hash Function which is built using the one-way function we saw in the previous session. What are the requirements for a
-
5.2. The Courtois-Finiasz-Sendrier (CFS) Construction
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session, I am going to present the Courtois-Finiasz-Sendrier Construction of a code-based digital signature. In the previous session, we have seen that it is impossible to hash a document
-
4.6. Attack against GRS codes
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session we will discuss the proposal of using generalized Reed-Solomon codes for the McEliece cryptosystem. As we have already said, generalized Reed-Solomon codes were proposed in 1986 by
-
5.5. Stern’s Zero-Knowledge Identification Scheme
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuIn this session, we are going to have a look at Stern’s Zero-Knowledge Identification Scheme. So, what is a Zero-Knowledge Identification Scheme? An identification scheme allows a prover to prove
-
4.9. Goppa codes still resist
Marquez-CorbellaIreneSendrierNicolasFiniaszMatthieuAll the results that we have seen this week doesn't mean that code based cryptography is broken. So in this session we will see that Goppa code still resists to all these attacks. So recall that
