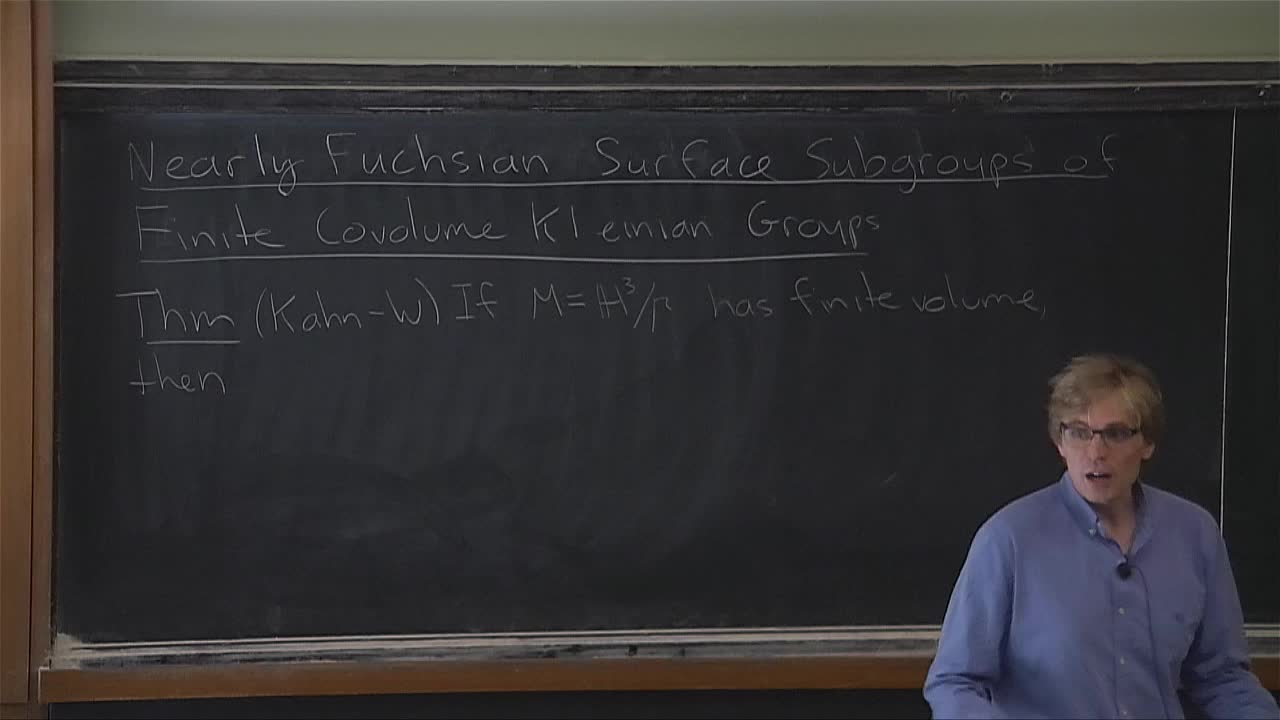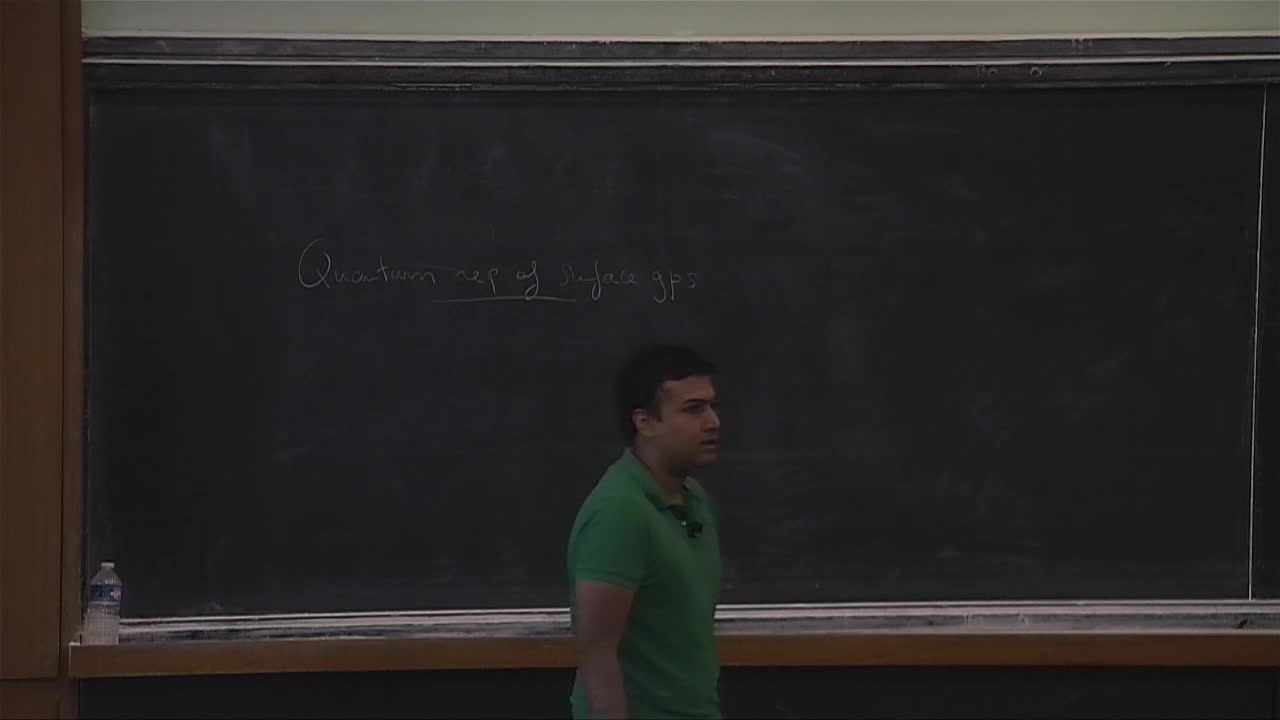2018

Vidéos
A. Zorich - Counting simple closed geodesics and volumes of moduli spaces (Part 3)
In the first two lectures I will try to tell (or, rather, to give an idea) of how Maryam Mirzakhani has counted simple closed geodesics on hyperbolic surfaces. I plan to briefly mention her
A. Zorich - Counting simple closed geodesics and volumes of moduli spaces (Part 1)
In the first two lectures I will try to tell (or, rather, to give an idea) of how Maryam Mirzakhani has counted simple closed geodesics on hyperbolic surfaces. I plan to briefly mention her
Ö. Yurttas - Algorithms for multicurves with Dynnikov coordinates
Multicurves have played a fundamental role in the study of mapping class groups of surfaces since the work of Dehn. A beautiful method of describing such systems on the n-punctured disk is given by
A. Wright - Mirzakhani's work on Earthquakes (Part 3)
We will give the proof of Mirzakhani's theorem that the earthquake flow and Teichmuller unipotent flow are measurably isomorphic. We will assume some familiarity with quadratic differentials, but no
A. Wright - Mirzakhani's work on Earthquakes (Part 2)
We will give the proof of Mirzakhani's theorem that the earthquake flow and Teichmuller unipotent flow are measurably isomorphic. We will assume some familiarity with quadratic differentials, but no
A. Wright - Mirzakhani's work on Earthquakes (Part 1)
We will give the proof of Mirzakhani's theorem that the earthquake flow and Teichmuller unipotent flow are measurably isomorphic. We will assume some familiarity with quadratic differentials, but no
J. Smillie - Horocycle dynamics (Part 2)
A major challenge in dynamics on moduli spaces is to understand the behavior of the horocycle flow. We will motivate this problem and discuss what is known and what is not known about it, focusing on
S. Skripchenko - Rauzy gasket, Arnoux-Yoccoz interval exchange map, Novikov's problem (Part 2)
1. Symbolic dynamics: Arnoux - Rauzy words and Rauzy gasket 2. Topology: Arnoux - Yoccoz example and its generalization 3. Novikov’s problem: how dynamics meets topology and together they help to
S.Schleimer - An introduction to veering triangulations
Singular euclidean structures on surfaces are a key tool in the study of the mapping class group, of Teichmüller space, and of kleinian three-manifolds. François Guéritaud, while studying work of Ian
C. Matheus - Square tiled surfaces (Part 2)
a) basic definitions and examples b) strata and genus c) reduced and primitive origamis, SL(2,R) action, Veech groups d) automorphisms and affine homeomorphisms e) homology of origamis f) Kontsevich
L. Liechti - Minimal dilatations on nonorientable surfaces
We discuss the problem of finding the minimal dilatation among pseudo-Anosov mapping classes on a fixed closed surface. In particular, for every nonorientable closed surface of even genus, we consider
C. Leininger - Teichmüller spaces and pseudo-Anosov homeomorphism (Part 3)
I will start by describing the Teichmuller space of a surface of finite type from the perspective of both hyperbolic and complex structures and the action of the mapping class group on it.
P. Hubert - Rauzy gasket, Arnoux-Yoccoz interval exchange map, Novikov's problem (Part 2)
1. Symbolic dynamics: Arnoux - Rauzy words and Rauzy gasket 2. Topology: Arnoux - Yoccoz example and its generalization 3. Novikov’s problem: how dynamics meets topology and together they help to
V. Gadre - Effective convergence of ergodic averages and cusp excursions of geodesics
Effective convergence of ergodic averages and cusp excursions of geodesics on moduli spaces We survey some applications of effective convergence of ergodic averages to the analysis of cusp ex
C.Fougeron - Diffusion rate for windtree models
Recent results on windtree models with polygonal obstacles have linked their diffusion rate with Lyapunov exponents in stata of quadratic differentials. The proves of these theorems follow from the
G. Forni - Cohomological equation and Ruelle resonnences (Part 2)
In these lectures we summarized results on the cohomological equation for translation flows on translation surfaces (myself, Marmi, Moussa and Yoccoz, Marmi and Yoccoz) and apply these results to the
S. Filip - K3 surfaces and Dynamics (Part 1)
K3 surfaces provide a meeting ground for geometry (algebraic, differential), arithmetic, and dynamics. I hope to discuss: Basic definitions and examples - Geometry (algebraic, differential, etc.) of
B. Deroin - Monodromy of algebraic families of curves (Part 2)
The mini-course will focus on the properties of the monodromies of algebraic families of curves defined over the complex numbers. One of the goal will be to prove the irreducibility of those
D. Davis - Periodic paths on the pentagon
Mathematicians have long understood periodic trajectories on the square billiard table. In the present work, we describe periodic trajectories on the regular pentagon – their geometry, symbolic
J. Aramayona - MCG and infinite MCG (Part 3)
The first part of the course will be devoted to some of the classical results about mapping class groups of finite-type surfaces. Topics may include: generation by twists, Nielsen-Thurston
J. Aramayona - MCG and infinite MCG (Part 2)
The first part of the course will be devoted to some of the classical results about mapping class groups of finite-type surfaces. Topics may include: generation by twists, Nielsen-Thurston
P. Apisa - Marked points in genus two and beyond
In the principal stratum in genus two, McMullen observed that something odd happens - there is only one nonarithmetic Teichmuller curve - the one generated by the decagon. This strange phenomenon
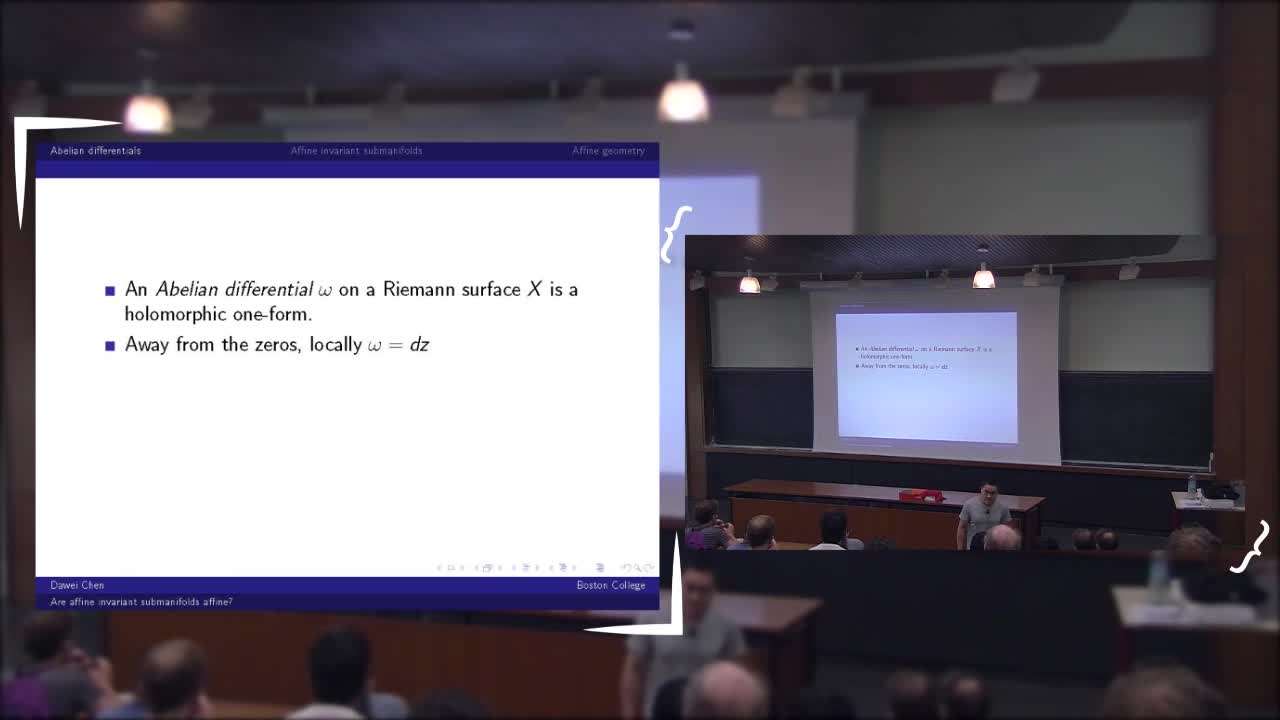
D. Chen - Are affine invariant submanifolds affine
We study the question whether affine invariant submanifolds arising from Teichmueller dynamics are affine varieties in the sense of algebraic geometry.
A. Wright - Nearly Fuchsian surface subgroups of finite covolume Kleinian groups
Multicurves have played a fundamental role in the study of mapping class groups of surfaces since the work of Dehn. A beautiful method of describing such systems on the n-punctured disk is given by
O. Paris-Romaskevich - Triangle tiling billiards
Tiling billiards is a dynamical system in which a billiard ball moves through the tiles of some fixed tiling in a way that its trajectory is a broken line, with breaks admitted only at the boundaries
R. Santharoubane - Quantum representations of surface groups
I will show how we can produce exotic representations of surface groups from the Witten-Reshetikhin-Turaev TQFT. These representations have infinite images and give points on character varieties that
I. Pasquinelli - Deligne-Mostow lattices and cone metrics on the sphere
Finding lattices in PU(n,1) has been one of the major challenges of the last decades. One way of constructing a lattice is to give a fundamental domain for its action on the complex hyperbolic space.
A. Lenzhen - Limit sets of Teichmuller geodesic rays in the Thurston boundary of Teichmuller space
H. Masur showed in the early 80s that almost every Teichmuller ray converges to a unique point in PMF. It is also known since a while that there are rays that have more than one accumulation point in
C. Judge - Systoles in translation surfaces
I will discuss joint work with Hugo Parlier concerning the shortest noncontractible loops—’systoles’—in a translation surface. In particular, we provide estimates (some sharp) on the number of
R. Gutierrez - Quaternionic monodromies of the Kontsevich–Zorich cocycle
The monodromy group of a translation surface M is the Lie group spanned by all symplectic matrices arising from the homological action of closed loops at M (inside its embodying orbit closure). In the
A. Eskin - Counting closed geodesics on translation surfaces
We show that the number of closed geodesics in the flat metric on a translation surface of length at most R is asymptotic to e hR / (hR). This is joint work with Kasra Rafi
A. Zorich - Counting simple closed geodesics and volumes of moduli spaces (Part 2)
In the first two lectures I will try to tell (or, rather, to give an idea) of how Maryam Mirzakhani has counted simple closed geodesics on hyperbolic surfaces. I plan to briefly mention her
B. Weiss - Horocycle dynamics (Part 2)
A major challenge in dynamics on moduli spaces is to understand the behavior of the horocycle flow. We will motivate this problem and discuss what is known and what is not known about it, focusing on
B. Weiss - Horocycle dynamics (Part 1)
A major challenge in dynamics on moduli spaces is to understand the behavior of the horocycle flow. We will motivate this problem and discuss what is known and what is not known about it, focusing on
J. Smillie - Horocycle dynamics (Part 1)
A major challenge in dynamics on moduli spaces is to understand the behavior of the horocycle flow. We will motivate this problem and discuss what is known and what is not known about it, focusing on
S. Skripchenko - Rauzy gasket, Arnoux-Yoccoz interval exchange map, Novikov's problem (Part 1)
1. Symbolic dynamics: Arnoux - Rauzy words and Rauzy gasket 2. Topology: Arnoux - Yoccoz example and its generalization 3. Novikov’s problem: how dynamics meets topology and together they help to
C. Matheus - Square tiled surfaces (Part 3)
a) basic definitions and examples b) strata and genus c) reduced and primitive origamis, SL(2,R) action, Veech groups d) automorphisms and affine homeomorphisms e) homology of origamis f) Kontsevich
C. Matheus - Square tiled surfaces (Part 1)
a) basic definitions and examples b) strata and genus c) reduced and primitive origamis, SL(2,R) action, Veech groups d) automorphisms and affine homeomorphisms e) homology of origamis f) Kontsevich
C. Leininger - Teichmüller spaces and pseudo-Anosov homeomorphism (Part 2)
I will start by describing the Teichmuller space of a surface of finite type from the perspective of both hyperbolic and complex structures and the action of the mapping class group on it. Then I will
C. Leininger - Teichmüller spaces and pseudo-Anosov homeomorphism (Part 1)
I will start by describing the Teichmuller space of a surface of finite type from the perspective of both hyperbolic and complex structures and the action of the mapping class group on it. Then I
P. Hubert - Rauzy gasket, Arnoux-Yoccoz interval exchange map, Novikov's problem (Part 1)
1. Symbolic dynamics: Arnoux - Rauzy words and Rauzy gasket 2. Topology: Arnoux - Yoccoz example and its generalization 3. Novikov’s problem: how dynamics meets topology and together they help to
G. Forni - Cohomological equation and Ruelle resonnences (Part 3)
In these lectures we summarized results on the cohomological equation for translation flows on translation surfaces (myself, Marmi, Moussa and Yoccoz, Marmi and Yoccoz) and apply these results to the
G. Forni - Cohomological equation and Ruelle resonnences (Part 1)
In these lectures we summarized results on the cohomological equation for translation flows on translation surfaces (myself, Marmi, Moussa and Yoccoz, Marmi and Yoccoz) and apply these results to the
S. Filip - K3 surfaces and Dynamics (Part 3)
K3 surfaces provide a meeting ground for geometry (algebraic, differential), arithmetic, and dynamics. I hope to discuss: - Basic definitions and examples - Geometry (algebraic, differential, etc.) of
S. Filip - K3 surfaces and Dynamics (Part 2)
K3 surfaces provide a meeting ground for geometry (algebraic, differential), arithmetic, and dynamics. I hope to discuss: - Basic definitions and examples - Geometry (algebraic, differential, etc.) of
B. Deroin - Monodromy of algebraic families of curves (Part 3)
The mini-course will focus on the properties of the monodromies of algebraic families of curves defined over the complex numbers. One of the goal will be to prove the irreducibility of those
B. Deroin - Monodromy of algebraic families of curves (Part 1)
The mini-course will focus on the properties of the monodromies of algebraic families of curves defined over the complex numbers. One of the goal will be to prove the irreducibility of those
J. Aramayona - MCG and infinite MCG (Part 1)
The first part of the course will be devoted to some of the classical results about mapping class groups of finite-type surfaces. Topics may include: generation by twists, Nielsen-Thurston
Intervenants et intervenantes
Mathématicien. Professeur assistant au département de Mathématiques de l'Université du Wisconsin (2018)
Co-directeur d'une thèse en Mathématiques à Aix-Marseille en 2016. Professeur à l'université autonome de Madrid (Espagne)
Mathématicien. Chercheur au département de mathématiques du Boston College, spécialiste de géométrie algébrique (2018)
Mathématicienne. En poste à Williams College, Williamstown, Mass. (en 2016). Professeure au Swarthmore College, université d'art libéraux (en 2021), Swarthmore, Etats-Unis
Chargé de recherche, Mathématiques - Université Paris Sud (Orsay)
Directeur de recherche à l'université de Cergy-Pontoise (en 2023)
Directeur d'une thèse de : mathématiques, Université Paris-Sud 11, Orsay (en 2011)
Président du jury d'une thèse en Mathématiques à Université Côte d'Azur en 2025
Mathématicien
Department of Mathematics, University of Chicago, IL, USA (en 2020)
Mathématicien
Professeur de mathématiques à l'Université du Maryland (Md.) en 2019
Auteur d'une thèse en Mathématiques à Sorbonne Paris Cité en 2017
Auteur d'une thèse en Mathématiques. Géométrie et dynamique à Sorbonne Paris Cité en 2019
Membre de l'équipe de mathématiques fondamentales du Laboratoire d'Analyse, Topologie et Probabilités. - Professeur HDR à la Faculté des Sciences et Techniques de Saint Jérôme, Université d' Aix Marseille (en 2019). Membre de l'Institut de Mathématiques de Marseille et du CIRM - Centre International de Rencontres Mathématiques (en 2023)
Rapporteur pour une thèse en Mathématiques soutenue à l'Université Grenoble Alpes en 2021
Maître de conférences à l'Université de Rennes 1. Membre de l'Institut de Recherche Mathématique de Rennes (IRMAR - UMR CNRS 6625) en 2019
Enseigne au département de mathématiques de l'université de Fribourg (2018)
Mathématicien. Titulaire d'une thèse en mathématiques obtenue à l'Université de Pise en 2000. En poste au département de mathématiques et informatique de l'Université de Udine, Italie (2000)
Mathématicien. Ater -post doctorat au Collège de France (2009). Directeur de Recherche au CNRS, Ecole Polytechnique en 2019
Auteure d'une thèse de doctorat de Mathématiques, Université de Lyon, 2016. Membre de jury de thèse. Chargée de recherche au CNRS à l'Institut de Mathématiques de Marseille en 2020
Mathématicienne britannique. Post-doctorante à l'Institut de mathématiques de Jussieu (2018)
Titulaire d'un doctorat de Mathématiques obtenu à Paris 7 en 2015
Professeur associé à l'institut de mathématiques de l'université de Warwick (2018)
Professeur de mathématiques, Harvard University en 2019
Enseigne à la faculté de Mathématiques de l'École des hautes études en sciences économiques de Moscou (2018)
Mathématicien. En poste : Departement of Mathematics, Cornell University, Ithaca NY, USA (en 2000)
Rapporteur pour une thèse en Mathématiques soutenue à Grenoble Alpes en 2019
Assistant Professor - Department of Physics, Engineering Physics & Astronomy - Queen’s University - Canada (en 2020)
Mathématicienne. En poste à l'université Dicle à Diyarbakır en Turquie (2018)
Mathématicien
Professeur à l'institut de mathématiques de l'université de Rennes 1 (IRMAR) (en 2003)
Professeur de mathématiques, Institut de Mathématiques de Jussieu - Paris Rive Gauche (IMJ-PRG) en 2019