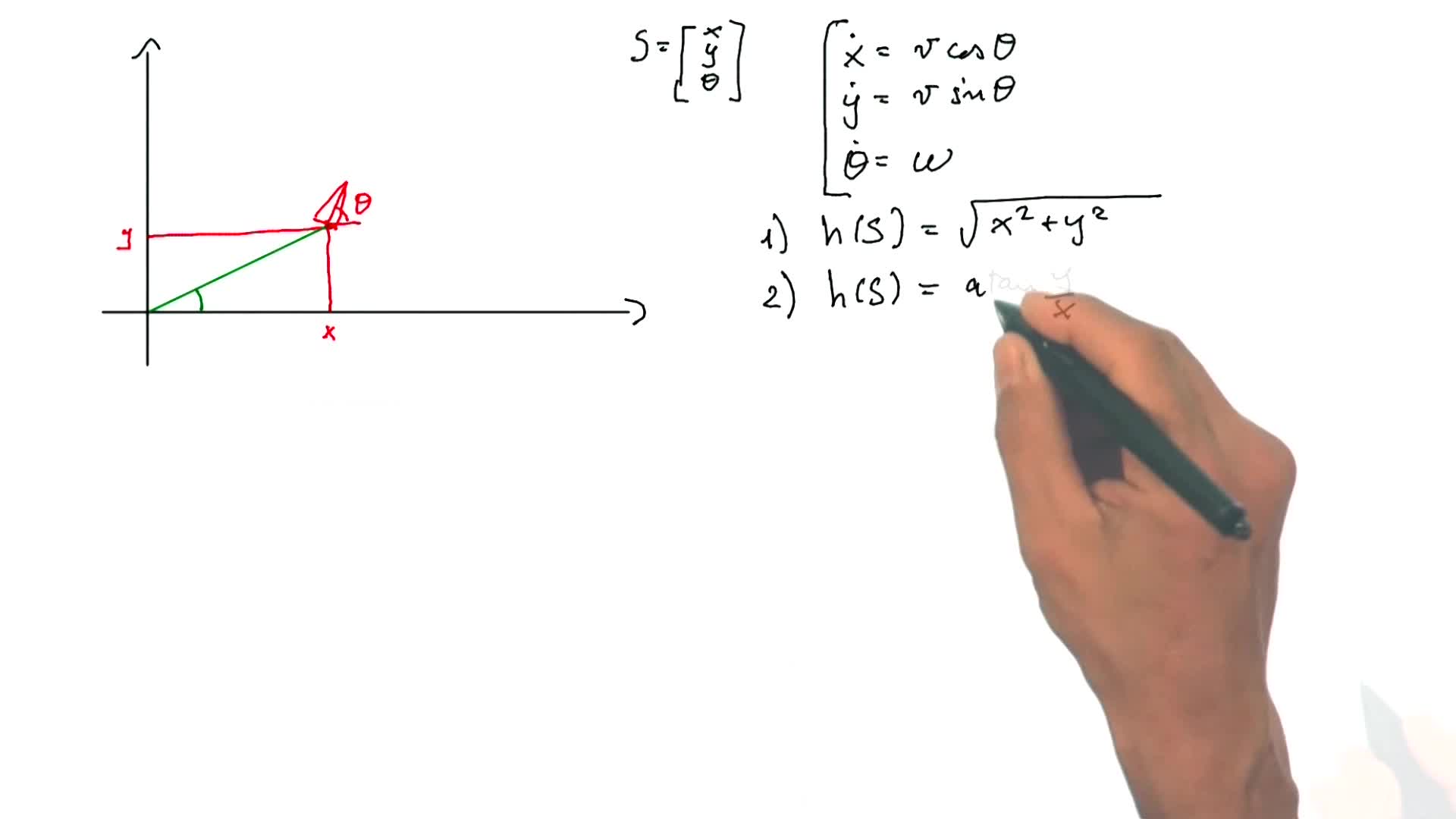Notice
3.2. Examples for the Perception in the EKF
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
In this video we discuss the secondtwo equations of the Kalman filter.
Intervention / Responsable scientifique
Thème
Documentation
Liens
Avec les mêmes intervenants et intervenantes
-
3.8. Applications of the Observability Rank Criterion
MartinelliAgostinoIn this video we want to apply the observability rank criterion to understand the observability properties of the system that we saw in the previous videos.
-
3.6. Observability in robotics
MartinelliAgostinoIn this video we discuss a fundamental issue which arises when we deal with an estimation problem: understanding if the system contains enough information to perform the estimation of the state.
-
3.5. Simultaneous Localization and Mapping (SLAM)
MartinelliAgostinoIn this video, we are discussing the SLAM problem: simultaneous localization and mapping.
-
3.7. Observability Rank Criterion
MartinelliAgostinoIn this video, we discuss an automatic method which is analytical and allows us to answer the question if a state is observable or not: this method is the Observability Rank Criterion which has
-
3.3. The EKF is a weight mean
MartinelliAgostinoIn this video I want to discuss the second two equations of the Kalman filter. And in particular I want to show that these actually perform a kind of weight mean.
-
3.4. The use of the EKF in robotics
MartinelliAgostinoIn this video I want to explain the steps that we have to follow in order to implement an extended Kalman filter in robotics.
-
3.1. Examples for the Action in the EKF
MartinelliAgostinoIn part 2, we have seen the equations of the Bayes filter, which are the general equations which allow us to update the probability distribution, as the data from both proprioceptive sensors and
-
2.1. Localization process in a probabilistic framework: basic concepts
MartinelliAgostinoIn this part, we will talk about localization which is a fundamental problem that a robot has to be able to solve in order to accomplish almost any tasks. In particular, we will start by
-
2.5. Reminds on probability
MartinelliAgostinoIn this sequence I want to remind you a few concepts in the theory of probability and then in the next one we finally derive the equations of the Bayes filter. So the concept that I want to
-
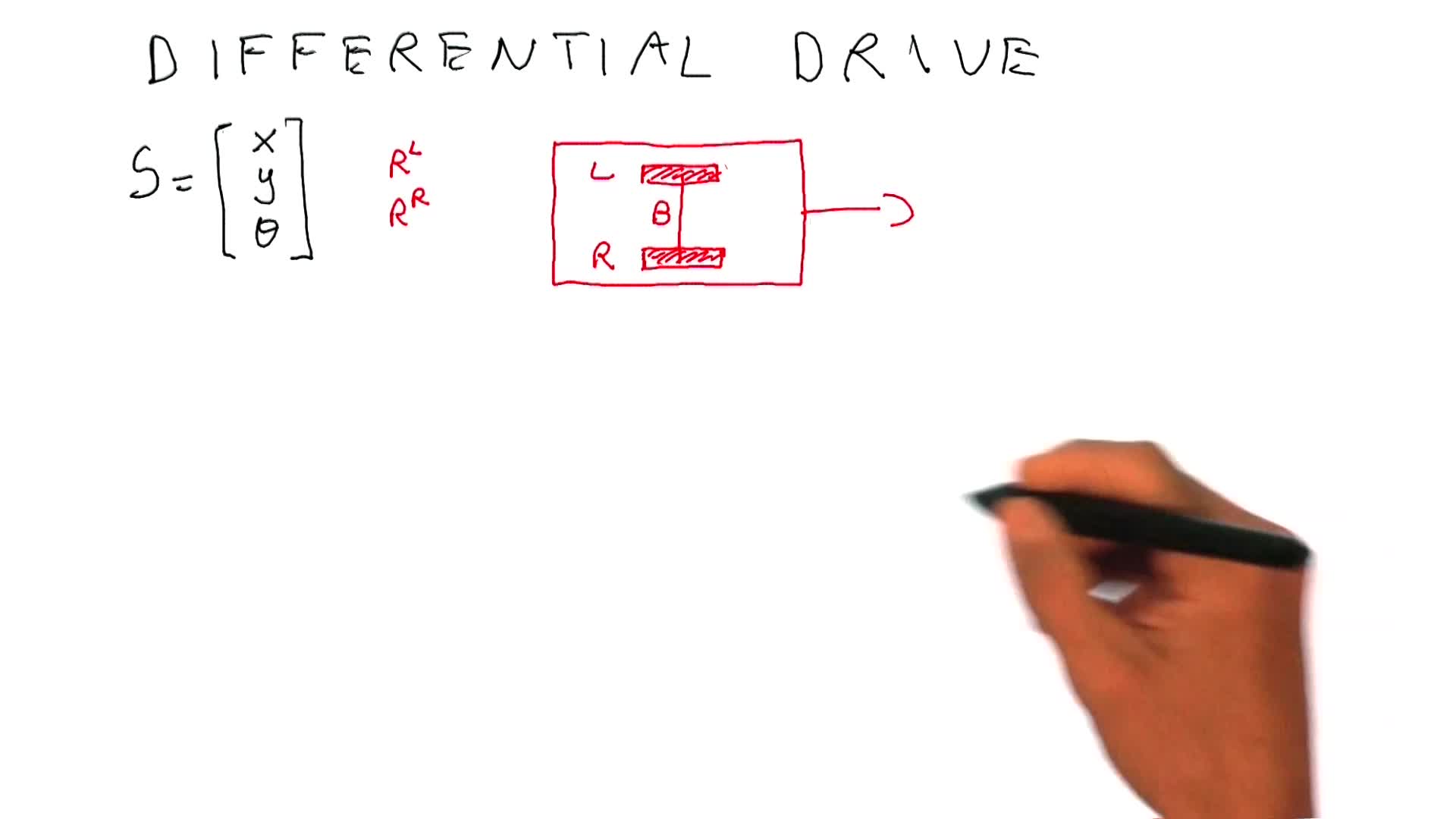
2.3. Wheel encoders for a differential drive vehicle
MartinelliAgostinoIn this video, we want to discuss the case of a wheel encoders in 2D, and in particular the case of a robot equipped with a differential drive which is very popular in mobile robotics.
-
2.8. The Extended Kalman Filter (EKF)
MartinelliAgostinoWe have seen the grid localization, and the advantage of this approach is that we can deal with any kind of probability distribution; in particular we don't need to do a Gaussian assumption. The
-
2.7. Grid Localization: an example in 1D
MartinelliAgostinoNow that we have the equations of the Bayes filter, we need a method in order to implement in real cases these equations. So, in the following, I want to discuss two methods, which are commonly
Sur le même thème
-
Et si l’intelligence artificielle déferlait sur les océans ?
L’évolution des technologies d’observation et de modélisation a joué un rôle central dans l’accroissement des connaissances sur le fonctionnement des océans ou dans le développement des activités
-
La vidéo sous-marine au service de la recherche halieutique
Accessible à de nombreuses applications, tant en biologie ou qu'en technologie des pêches, la vidéo sous-marine est de plus en plus utilisée dans le domaine de la recherche halieutique. Les progrès
-
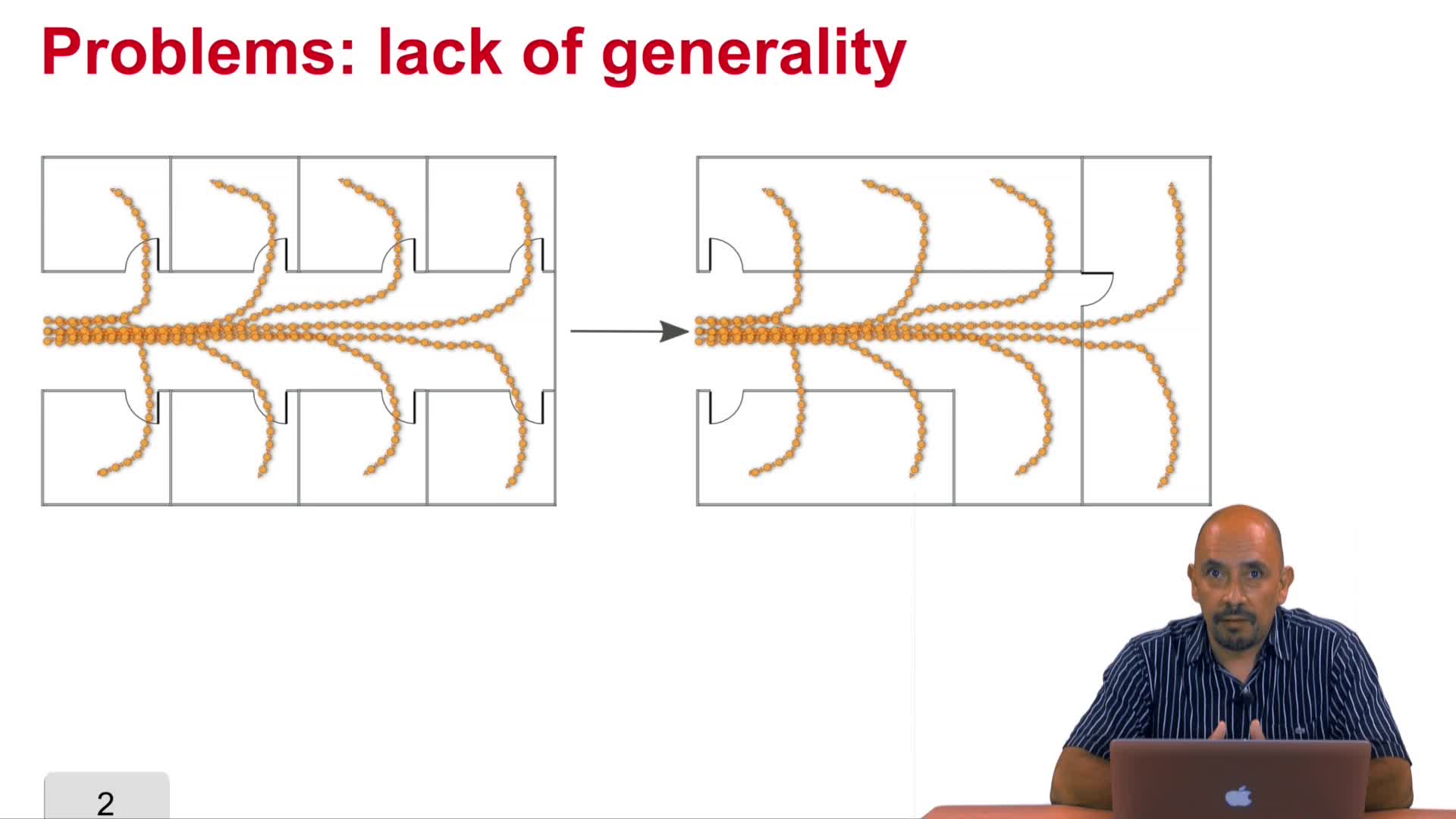
5.7. Typical Trajectories: drawbacks
Vasquez GoveaAlejandro DizanIn previous videos we have discussed how to implement the typical trajectories and motion patterns approach. In this video we are going to discuss what are the drawbacks of such an approach,
-
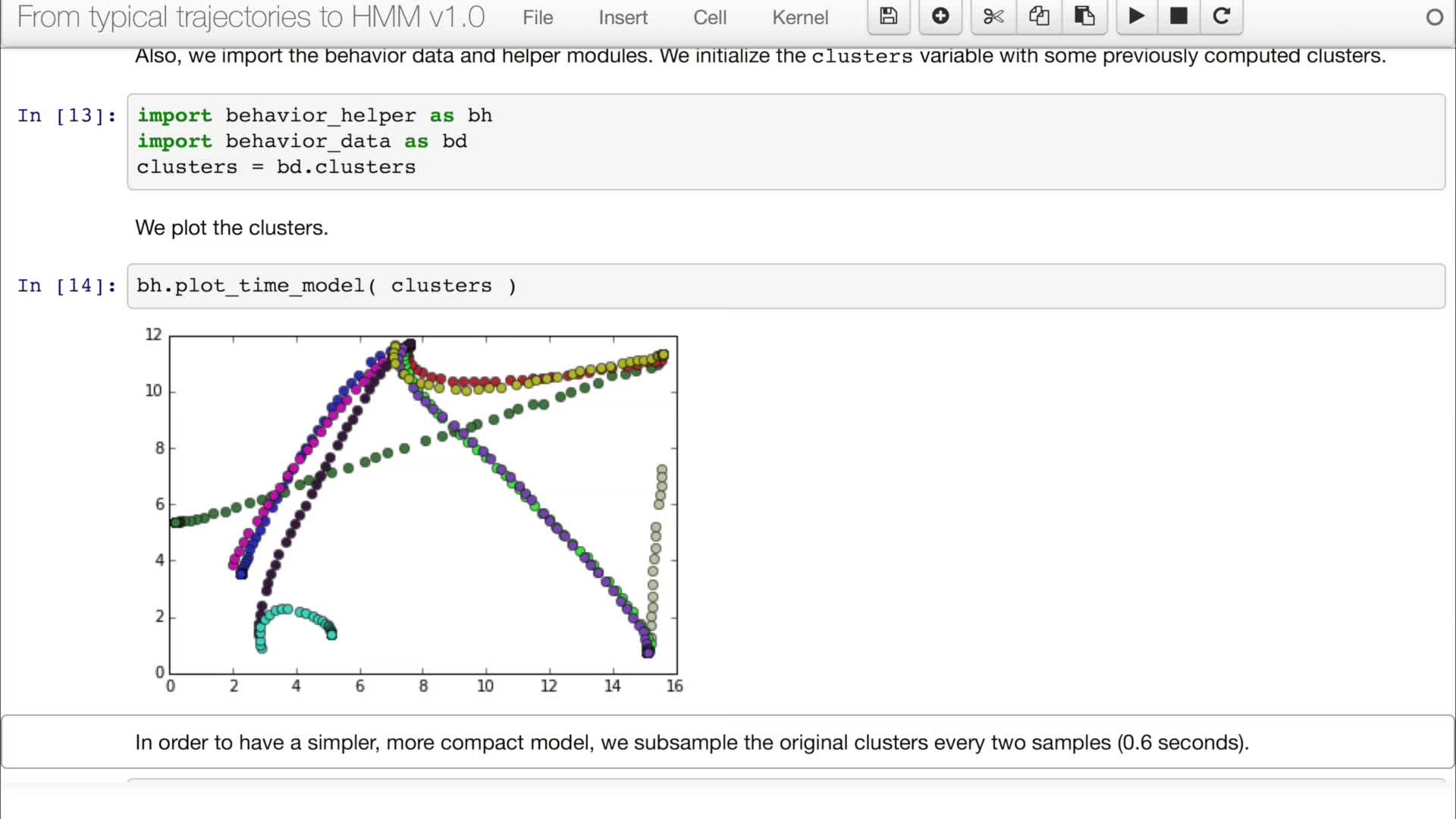
5.5. From trajectories to discrete time-state models
Vasquez GoveaAlejandro DizanIn this video we are going to apply the concepts we have reviewed in the video 5.4 into real trajectories.
-
5.8. Other approaches: Social Forces
Vasquez GoveaAlejandro DizanIn this video we will review one of the alternatives we are proposing to the use of Hidden Markov models and typical trajectories: the Social Force model.
-
5.6. Predicting Human Motion
Vasquez GoveaAlejandro DizanIn video 5.5 we have defined an HMM in Python. In this video we are going to learn how to use it to estimate and predict motion.
-
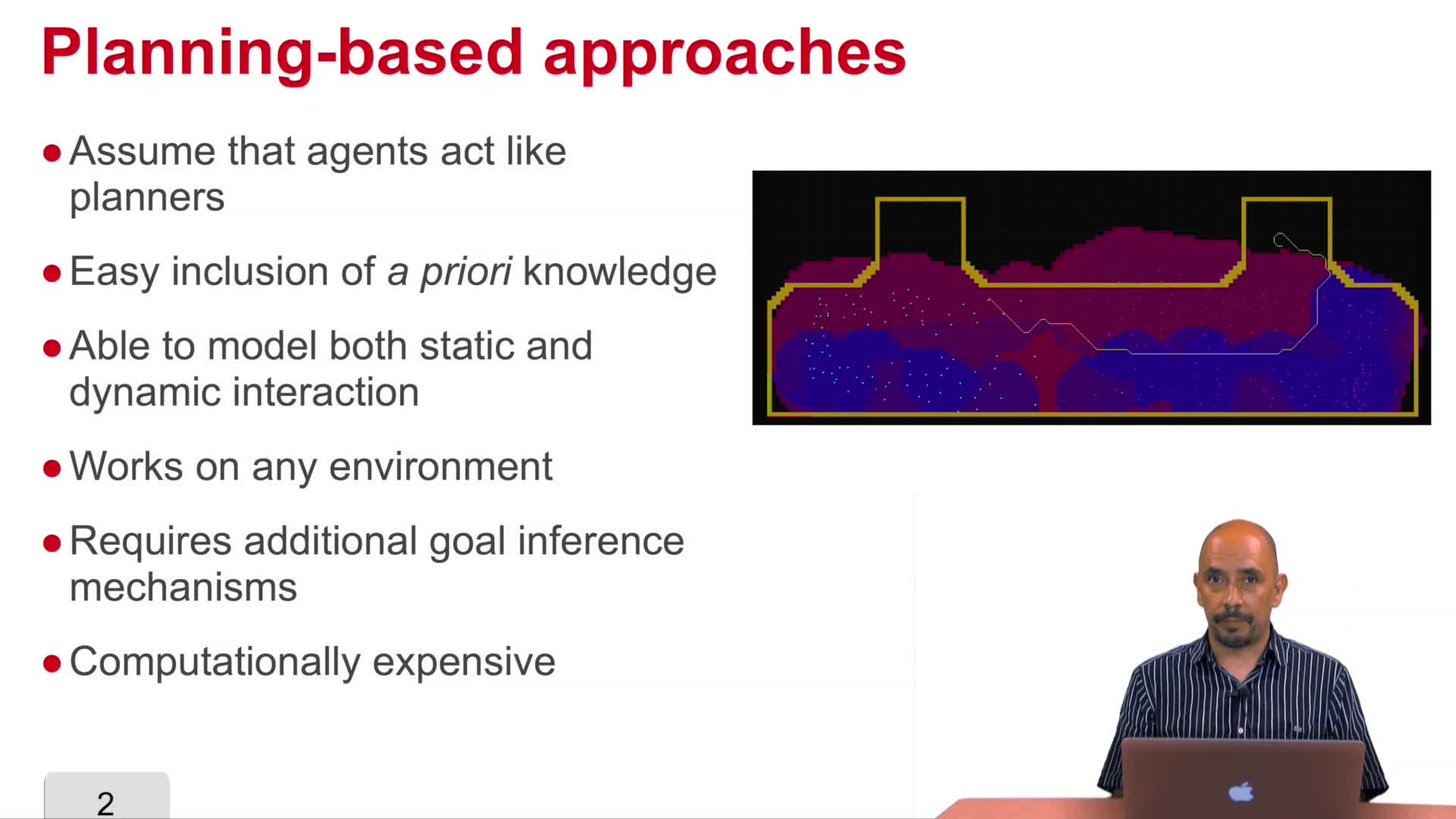
5.9. Other approaches: Planning-based approaches
Vasquez GoveaAlejandro DizanIn this video we are going to study a second, and probably the most promising alternative for motion prediction: planning-based algorithms.
-
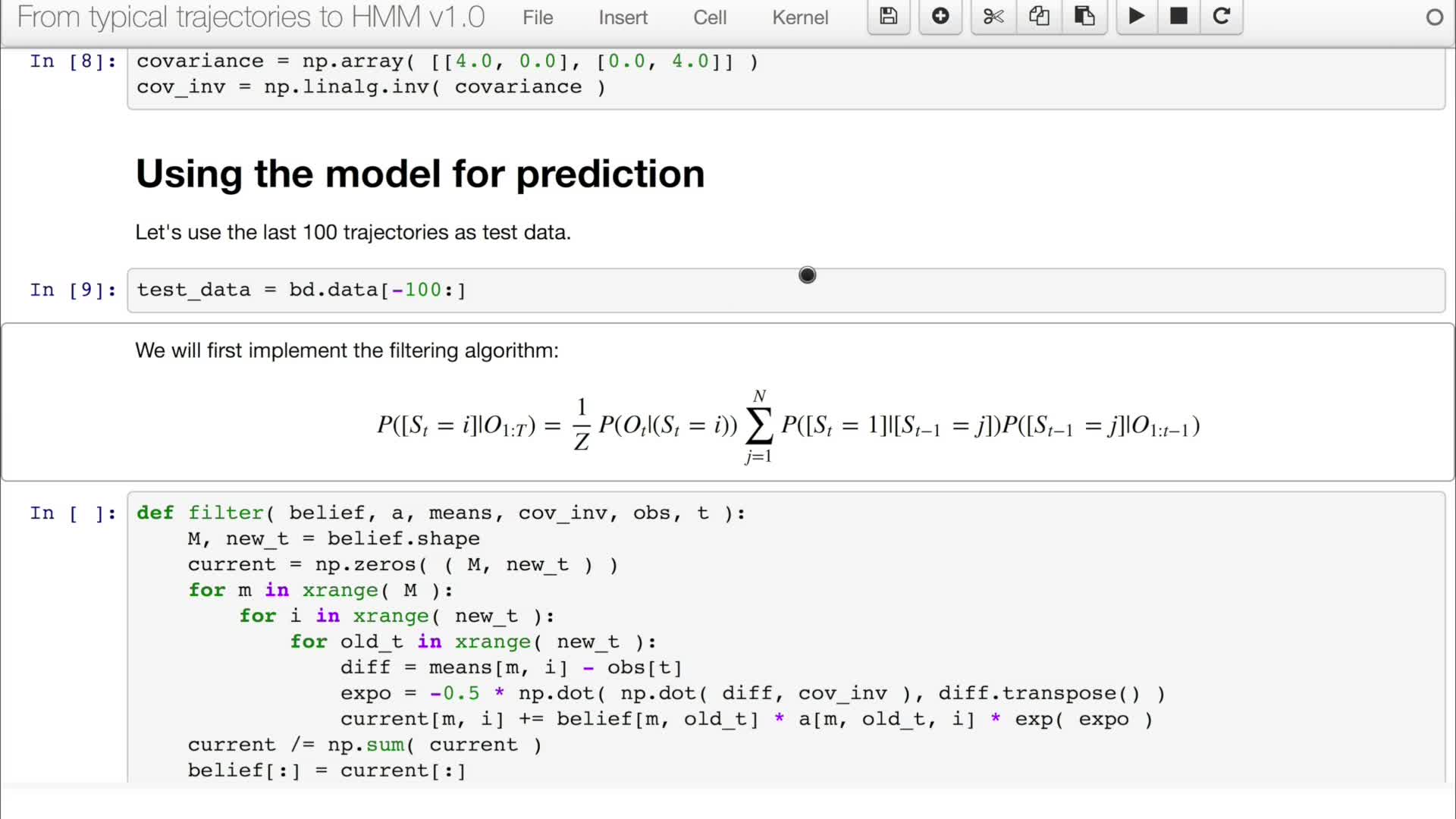
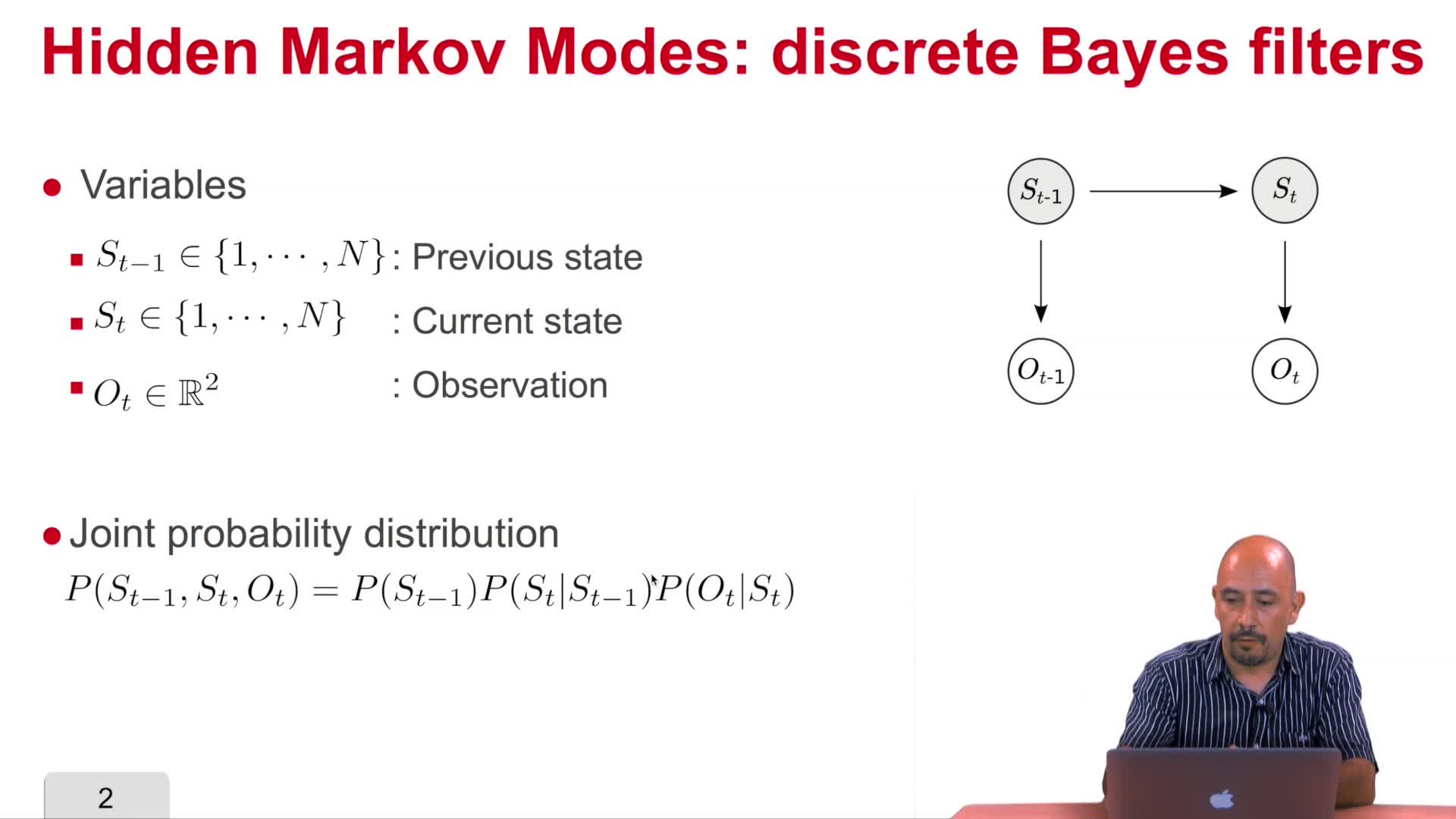
5.4. Bayesian filter inference
Vasquez GoveaAlejandro DizanIn this video we will review the base filter and we will study a particular instance of the Bayesian filter called Hidden Markov models which is a discrete version of a Bayesian filter.
-
4.2. Dynamic Probabilistic Grids – Bayesian Occupancy Filter concept
LaugierChristianThis video will show how to describe Bayesian occupancy filter concept.
-
4.8. Situation Awareness – Problem statement and Motion / Prediction Models
LaugierChristianThis videos addresses the problem of situation awareness and motion prediction models.
-
4.4. Object level Perception functions (SLAM + DATMO)
LaugierChristianThis video is dedicated to the object level perception functions: Simultaneous Localization Mapping (SLAM) and Detection and Tracking surrounding Mobile Objects (DATMO).
-
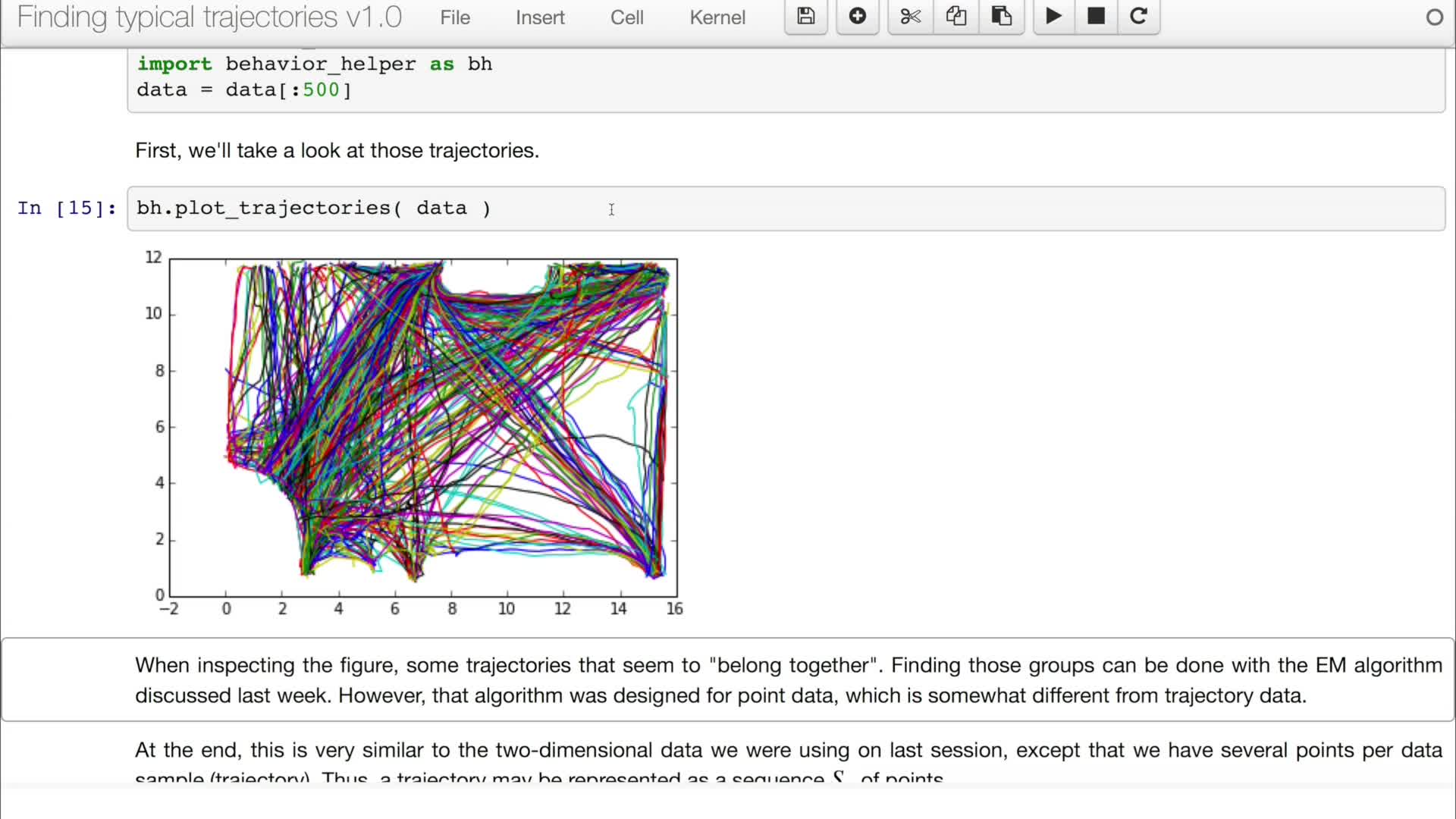
5.3a. Learning typical trajectories 1/2
Vasquez GoveaAlejandro DizanIn video 5.2 we showed how to apply the expectation maximization clustering algorithm to two-dimensional data. In this video we will learn how to apply it to trajectory data. And then we will be