4: Key Attacks

Descriptif
Table of contents
4.1. Introduction
4.2. Support Splitting Algorithm
4.3. Distinguisher for GRS codes
4.4. Attack against subcodes of GRS codes
4.5. Error-Correcting Pairs
4.6. Attack against GRS codes
4.7. Attack against Reed-Muller codes
4.8. Attack against Algebraic Geometry codes
4.9. Goppa codes still resist
Vidéos
4.1. Introduction
Welcome to the fourth week of the MOOC Code-based Cryptography. Recall that we have mainly two ways of cryptanalyzing in the McEliece cryptosystem. We have Message Attacks, which address the problem
4.2. Support Splitting Algorithm
This session will be about the support splitting algorithm. For the q-ary case, there are three different notions of equivalence. The general one: two codes of length n are semi-linear equivalent
4.3. Distinguisher for GRS codes
In this session we will see that generalized Reed-Solomon codes behave differently than random codes with respect to the star operation. Thus we can define a distinguisher for Generalized Reed
4.4. Attack against subcodes of GRS codes
In this session, we will talk about using subcodes of a Generalized Reed–Solomon code for the McEliece Cryptosystem. Recall that to avoid the attack of Sidelnikov and Shestakov, Berger and
4.5. Error-Correcting Pairs
We present in this session a general decoding method for linear codes. And we will see it in an example. Let C be a generalized Reed-Solomon code of dimension k associated to the pair (c, d). Then,
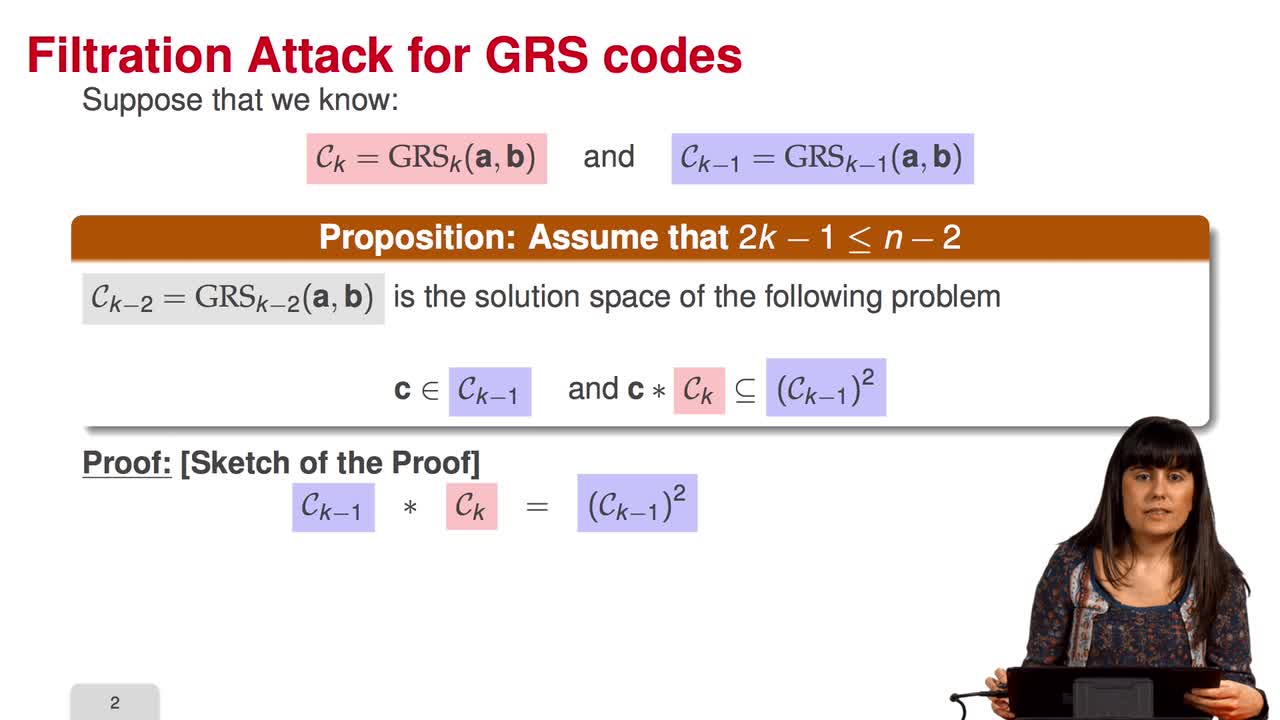
4.6. Attack against GRS codes
In this session we will discuss the proposal of using generalized Reed-Solomon codes for the McEliece cryptosystem. As we have already said, generalized Reed-Solomon codes were proposed in 1986 by
4.7. Attack against Reed-Muller codes
In this session, we will introduce an attack against binary Reed-Muller codes. Reed-Muller codes were introduced by Muller in 1954 and, later, Reed provided the first efficient decoding algorithm
4.9. Goppa codes still resist
All the results that we have seen this week doesn't mean that code based cryptography is broken. So in this session we will see that Goppa code still resists to all these attacks. So recall that
4.8. Attack against Algebraic Geometry codes
In this session, we will present an attack against Algebraic Geometry codes (AG codes). Algebraic Geometry codes is determined by a triple. First of all, an algebraic curve of genus g, then a n
Intervenants et intervenantes
Auteur d'une thèse en mathématiques et informatique à l'Ecole polytechnique de Paris
Chercheuse à la faculté des sciences de l'université de La Laguna. Spécialités : code, cryptograhie et algèbre informatique (2015)
Enseignant chercheur en informatique à l'INRIA. Thèmes de recherche : Codes correcteurs d'erreurs et Cryptographie.