Notice
4.7. Attack against Reed-Muller codes
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
In this session, we willintroduce an attack against binary Reed-Muller codes. Reed-Muller codes wereintroduced by Muller in 1954 and, later, Reed provided thefirst efficient decoding algorithm for these codes. Reed-Muller are just ageneralization of generalized Reed-Solomon codes. Generalized Reed-Solomoncodes are evaluation of univariate polynomials,and Reed-Muller codes are evaluation ofmultivariate polynomials. We will study binary Reed-Muller codes. The binary Reed-Mullerconsists of the set of codewords obtained by evaluating all theBoolean functions of degree r with m variables. Thus, theblock length of this code is 2^m. The dimension is anumber of polynomials of degree r with binary coefficient, andthe minimum distance is 2^m - r. Let us study two examples. The first example is aReed-Muller associated to the evaluation of all monomialsof degree 1 in three variables. The vectors associatedto these monomials are the following ones, which gives agenerator matrix of the code. This code has parameters:length 8, dimension 4, and minimum distance 4, thatis, it detects two errors and correct just one error.Take notice that the matrix of a Reed-Muller code withdegree bound 1 has a particular form. If we remove the firstrow, then we have at the i-th column just the number i-1read as a binary number. And this property willbe the key of the attack. Now, we have another example. We have the binaryReed-Muller code associated to the evaluation of monomialsof degree up to 2 in four variables. The vectorsassociated to this monomial are the following ones, which givea generator matrix of the code. This code has length 16,dimension 11, and minimum distance 4. Let us see someproperties of Reed-Muller code. First of all, we have thefollowing decreasing sequence. The code with the same degreebound as variables is the whole space. And moreover, the dual of aReed-Muller code is again a Reed-Muller code. And the proof is very easy.Just note that the dimension of the sum of these twocodes is 2^n, that is, the whole space. Moreover, the starproduct of these two codes is
- this special code, which isthe code with all even weight vectors.
Intervention
Dans la même collection
-
4.6. Attack against GRS codes
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In this session we will discuss the proposal of using generalized Reed-Solomon codes for the McEliece cryptosystem. As we have already said, generalized Reed-Solomon codes were proposed in 1986 by
-
4.4. Attack against subcodes of GRS codes
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In this session, we will talk about using subcodes of a Generalized Reed–Solomon code for the McEliece Cryptosystem. Recall that to avoid the attack of Sidelnikov and Shestakov, Berger and
-
4.9. Goppa codes still resist
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
All the results that we have seen this week doesn't mean that code based cryptography is broken. So in this session we will see that Goppa code still resists to all these attacks. So recall that
-
4.5. Error-Correcting Pairs
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
We present in this session a general decoding method for linear codes. And we will see it in an example. Let C be a generalized Reed-Solomon code of dimension k associated to the pair (c, d). Then,
-
4.8. Attack against Algebraic Geometry codes
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In this session, we will present an attack against Algebraic Geometry codes (AG codes). Algebraic Geometry codes is determined by a triple. First of all, an algebraic curve of genus g, then a n
-
4.1. Introduction
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
Welcome to the fourth week of the MOOC Code-based Cryptography. Recall that we have mainly two ways of cryptanalyzing in the McEliece cryptosystem. We have Message Attacks, which address the problem
-
4.2. Support Splitting Algorithm
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
This session will be about the support splitting algorithm. For the q-ary case, there are three different notions of equivalence. The general one: two codes of length n are semi-linear equivalent
-
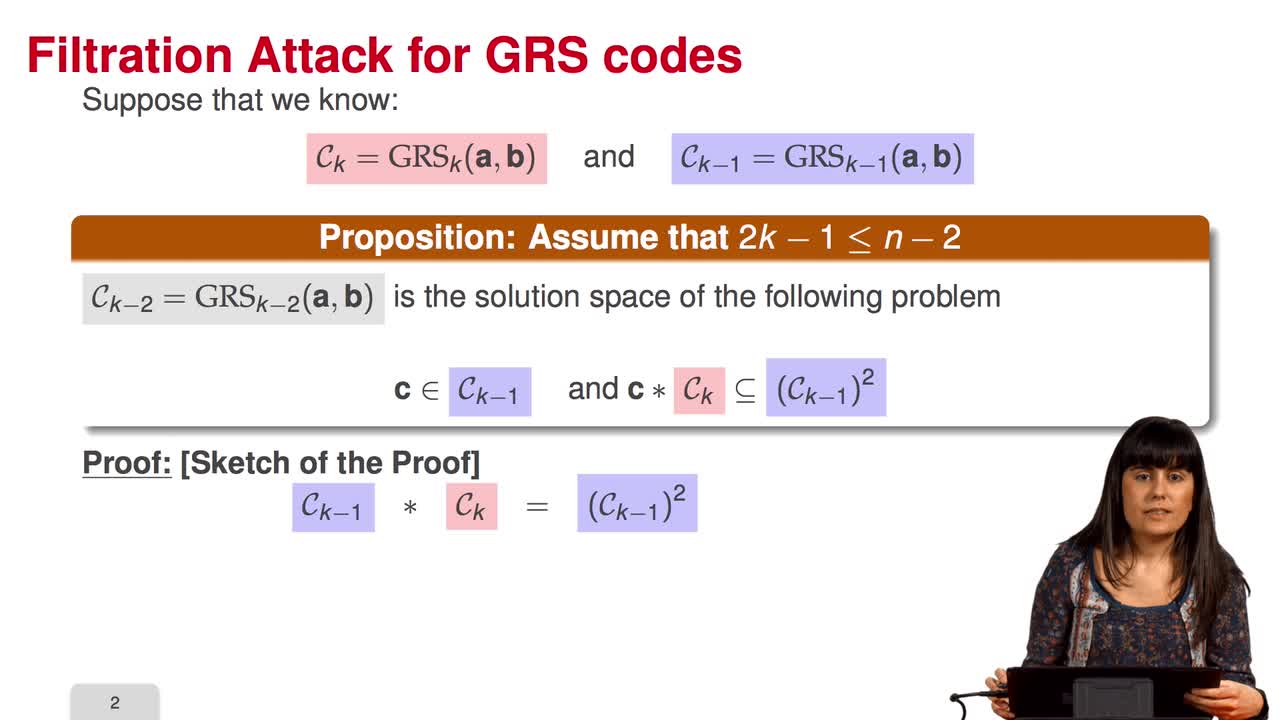
4.3. Distinguisher for GRS codes
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In this session we will see that generalized Reed-Solomon codes behave differently than random codes with respect to the star operation. Thus we can define a distinguisher for Generalized Reed
Avec les mêmes intervenants et intervenantes
-
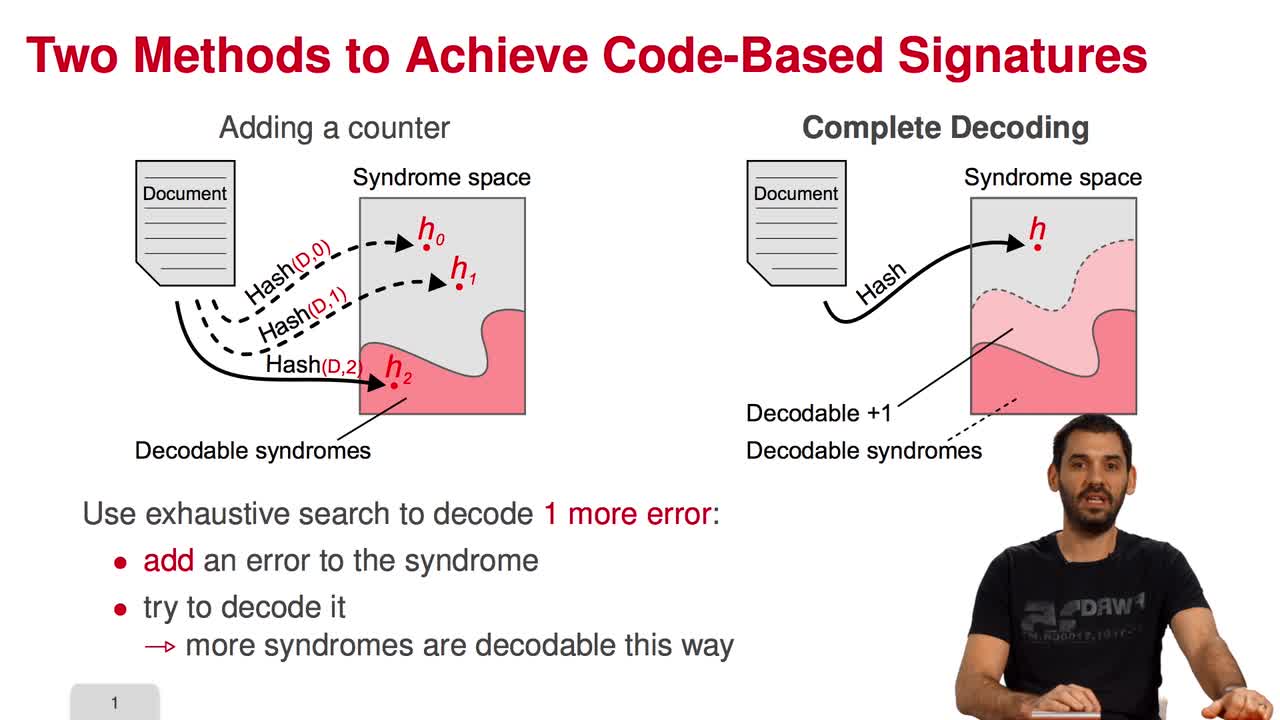
5.2. The Courtois-Finiasz-Sendrier (CFS) Construction
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In this session, I am going to present the Courtois-Finiasz-Sendrier Construction of a code-based digital signature. In the previous session, we have seen that it is impossible to hash a document
-
4.5. Error-Correcting Pairs
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
We present in this session a general decoding method for linear codes. And we will see it in an example. Let C be a generalized Reed-Solomon code of dimension k associated to the pair (c, d). Then,
-
5.5. Stern’s Zero-Knowledge Identification Scheme
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In this session, we are going to have a look at Stern’s Zero-Knowledge Identification Scheme. So, what is a Zero-Knowledge Identification Scheme? An identification scheme allows a prover to prove
-
4.9. Goppa codes still resist
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
All the results that we have seen this week doesn't mean that code based cryptography is broken. So in this session we will see that Goppa code still resists to all these attacks. So recall that
-
5.3. Attacks against the CFS Scheme
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In this session, we will have a look at the attacks against the CFS signature scheme. As for public-key encryption, there are two kinds of attacks against signature schemes. First kind of attack is
-
4.6. Attack against GRS codes
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In this session we will discuss the proposal of using generalized Reed-Solomon codes for the McEliece cryptosystem. As we have already said, generalized Reed-Solomon codes were proposed in 1986 by
-
5.6. An Efficient Provably Secure One-Way Function
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In this session, we are going to see how to build an efficient provably secure one-way function from coding theory. As you know, a one-way function is a function which is simple to evaluate and
-
5.1. Code-Based Digital Signatures
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
Welcome to the last week of this MOOC on code-based cryptography. This week, we will be discussing other cryptographic constructions relying on coding theory. We have seen how to do public key
-
4.4. Attack against subcodes of GRS codes
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In this session, we will talk about using subcodes of a Generalized Reed–Solomon code for the McEliece Cryptosystem. Recall that to avoid the attack of Sidelnikov and Shestakov, Berger and
-
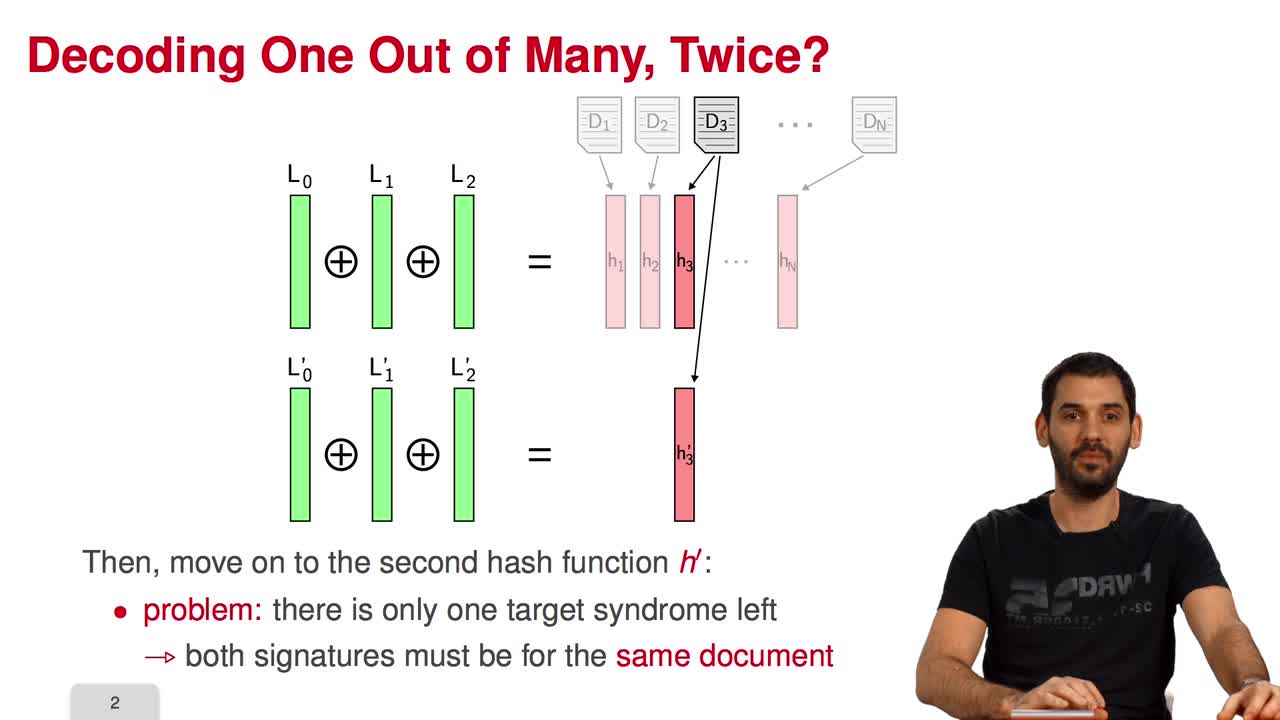
5.4. Parallel-CFS
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In this session, I will present a variant of the CFS signature scheme called parallel-CFS. We start from a simple question: what happens if you try to use two different hash functions and compute
-
4.8. Attack against Algebraic Geometry codes
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In this session, we will present an attack against Algebraic Geometry codes (AG codes). Algebraic Geometry codes is determined by a triple. First of all, an algebraic curve of genus g, then a n
-
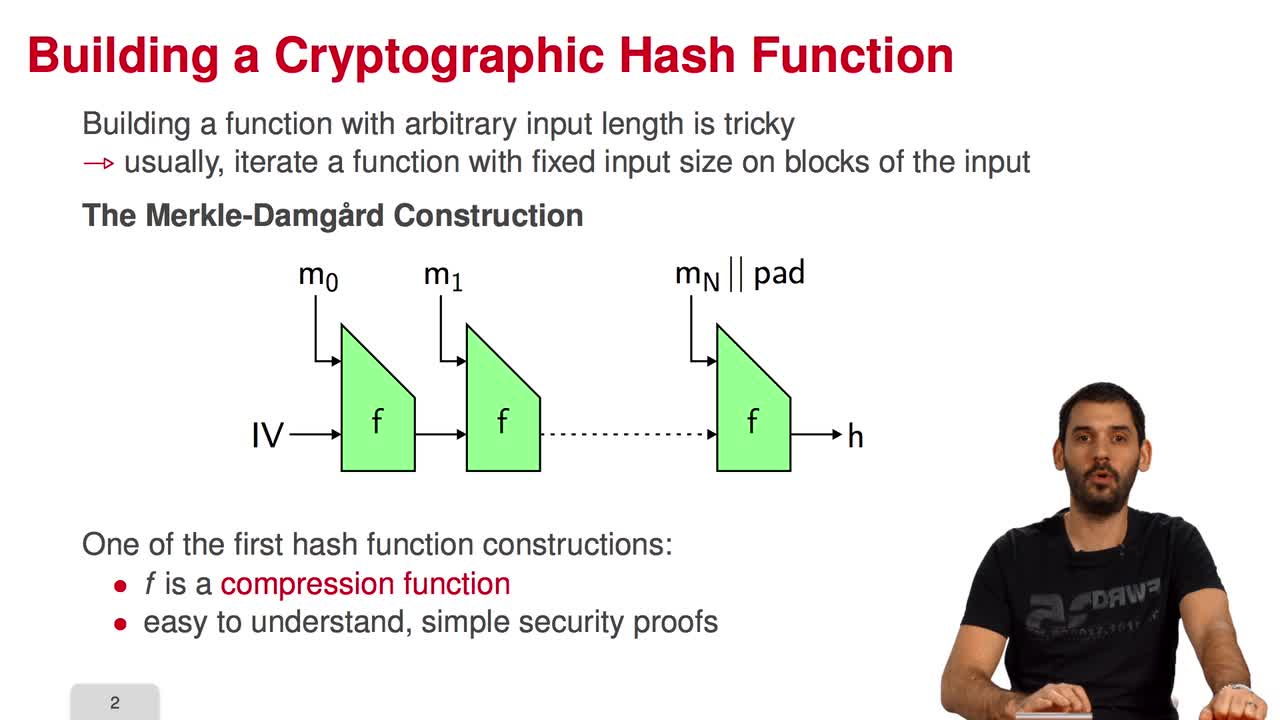
5.7. The Fast Syndrome-Based (FSB) Hash Function
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In the last session of this week, we will have a look at the FSB Hash Function which is built using the one-way function we saw in the previous session. What are the requirements for a
Sur le même thème
-
Machines algorithmiques, mythes et réalités
MAZENOD Vincent
Vincent Mazenod, informaticien, partage le fruit de ses réflexions sur l'évolution des outils numériques, en lien avec les problématiques de souveraineté, de sécurité et de vie privée...
-
Désassemblons le numérique - #Episode11 : Les algorithmes façonnent-ils notre société ?
SCHWARTZ Arnaud
LIMA PILLA Laércio
ESTéRIE Pierre
SALLET Frédéric
FERBOS Aude
ROUMANOS Rayya
CHRAIBI KADOUD Ikram
Un an après le tout premier hackathon sur les méthodologies d'enquêtes journalistiques sur les algorithmes, ce nouvel épisode part à la rencontre de différents points de vue sur les algorithmes.
-
Les machines à enseigner. Du livre à l'IA...
BRUILLARD Éric
Que peut-on, que doit-on déléguer à des machines ? C'est l'une des questions explorées par Éric Bruillard qui, du livre aux IA génératives, expose l'évolution des machines à enseigner...
-
Quel est le prix à payer pour la sécurité de nos données ?
MINAUD Brice
À l'ère du tout connecté, la question de la sécurité de nos données personnelles est devenue primordiale. Comment faire pour garder le contrôle de nos données ? Comment déjouer les pièges de plus en
-
Désassemblons le numérique - #Episode9 : Bientôt des supercalculateurs dans nos piscines ?
BEAUMONT Olivier
BOUZEL Rémi
Des supercalculateurs feraient-ils bientôt leur apparition dans les piscines municipales pour les chauffer ? Réponses d'Olivier Beaumont, responsable de l'équipe-projet Topal, et Rémi Bouzel,
-
Des systèmes de numération pour le calcul modulaire
BAJARD Jean-Claude
Le calcul modulaire est utilisé dans de nombreuses applications des mathématiques, telles que la cryptographie. La réduction modulaire dans un contexte très général est coûteuse, car elle n
-
Projection methods for community detection in complex networks
LITVAK Nelly
Community detection is one of most prominent tasks in the analysis of complex networks such as social networks, biological networks, and the world wide web. A community is loosely defined as a group
-
Lara Croft. doing fieldwork under surveillance
DALL'AGNOLA Jasmin
Lara Croft. Doing Fieldwork Under Surveillance Intervention de Jasmin Dall'Agnola (The George Washington University), dans le cadre du Colloque coorganisé par Anders Albrechtslund, professeur en
-
Containing predictive tokens in the EU
CZARNOCKI Jan
Containing Predictive Tokens in the EU – Mapping the Laws Against Digital Surveillance, intervention de Jan Czarnocki (KU Leuven), dans le cadre du Colloque coorganisé par Anders Albrechtslund,
-
Inauguration de l'exposition - Vanessa Vitse : Nombres de Sophie Germain et codes secrets
VITSE Vanessa
Exposé de Vanessa Vitse (Institut Fourier) : Nombres de Sophie Germain et codes secrets
-
"Le mathématicien Petre (Pierre) Sergescu, historien des sciences, personnalité du XXe siècle"
HERLéA Alexandre
Alexandre HERLEA est membre de la section « Sciences, histoire des sciences et des techniques et archéologie industrielle » du CTHS. Professeur émérite des universités, membre effectif de l'Académie
-
Ivan Murit - Processus de création d'images
MURIT Ivan
Je vais présenter une manière décalée d'aborder les outils d'impression. Pour cela nous ne partirons pas de l'envie d'imprimer une image préexistante, mais d'avant cela : comment se crée une forme
