1: Error-Correcting Codes and Cryptography

Descriptif
Table of contents
1.1. Introduction I - Cryptography
1.2. Introduction II - Coding Theory
1.3. Encoding (Linear Transformation)
1.4. Parity Checking
1.5. Error Correcting Capacity
1.6. Decoding (A Difficult Problem)
1.7. Reed-Solomon Codes
1.8. Goppa Codes
1.9. McEliece Cryptosystem
Vidéos
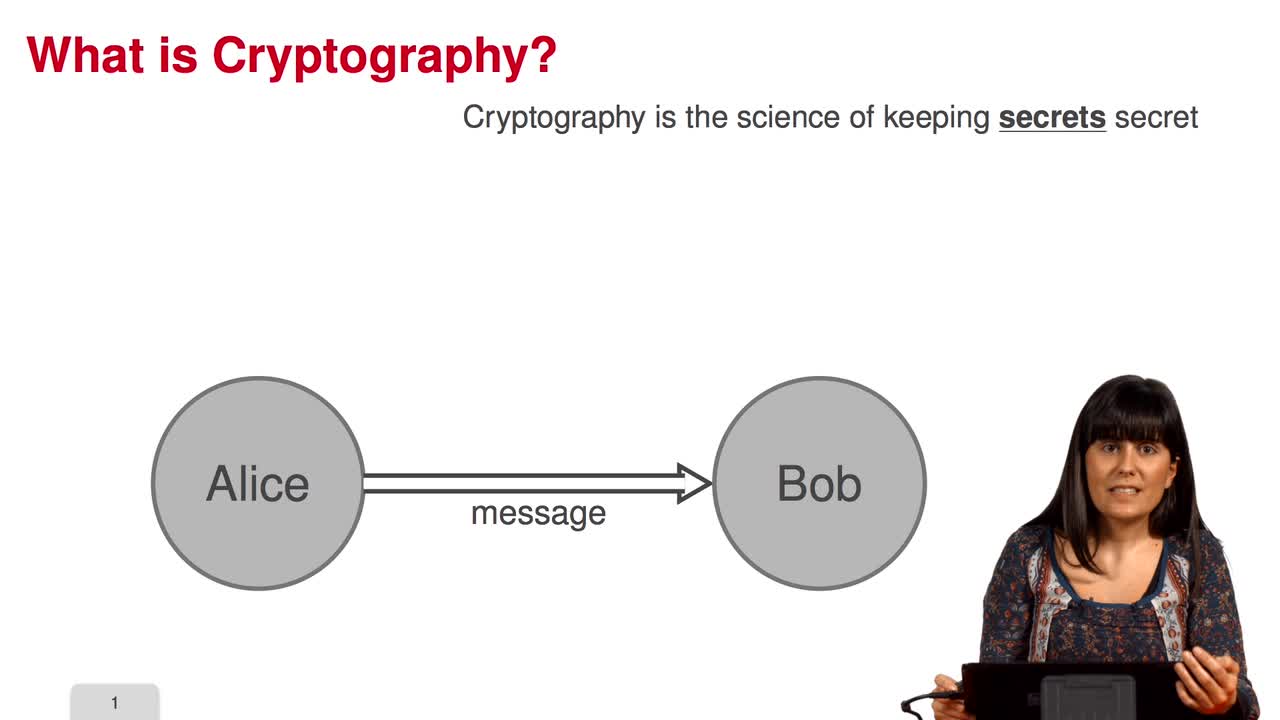
1.1. Introduction I - Cryptography
Welcome to this MOOC which is entitled: code-based cryptography. This MOOC is divided in five weeks. The first week, we will talk about error-correcting codes and cryptography, this is an introduction
1.2. Introduction II - Coding Theory
In this session, we will give a brief introduction to Coding Theory. Claude Shannon's paper from 1948 entitled "A Mathematical Theory of Communication" gave birth to the disciplines of Information
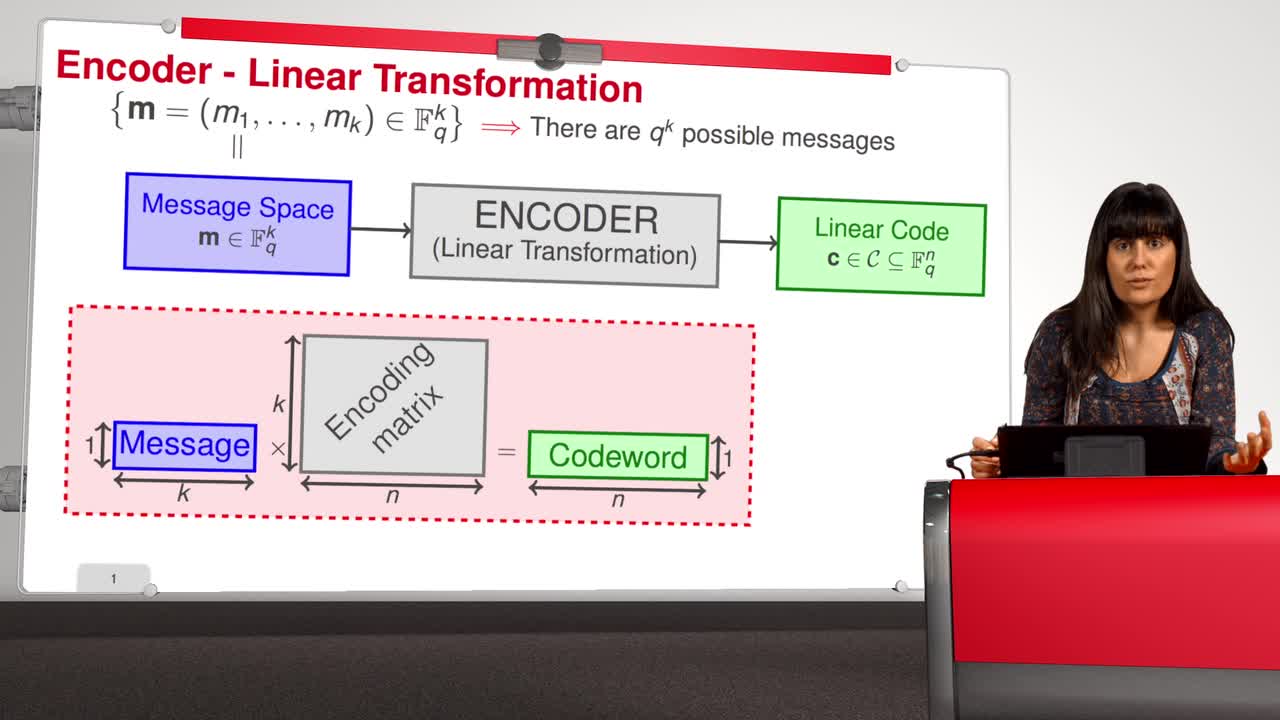
1.3. Encoding (Linear Transformation)
In this session, we will talk about the easy map of the - one-way trapdoor functions based on error-correcting codes. We suppose that the set of all messages that we wish to transmit is the set
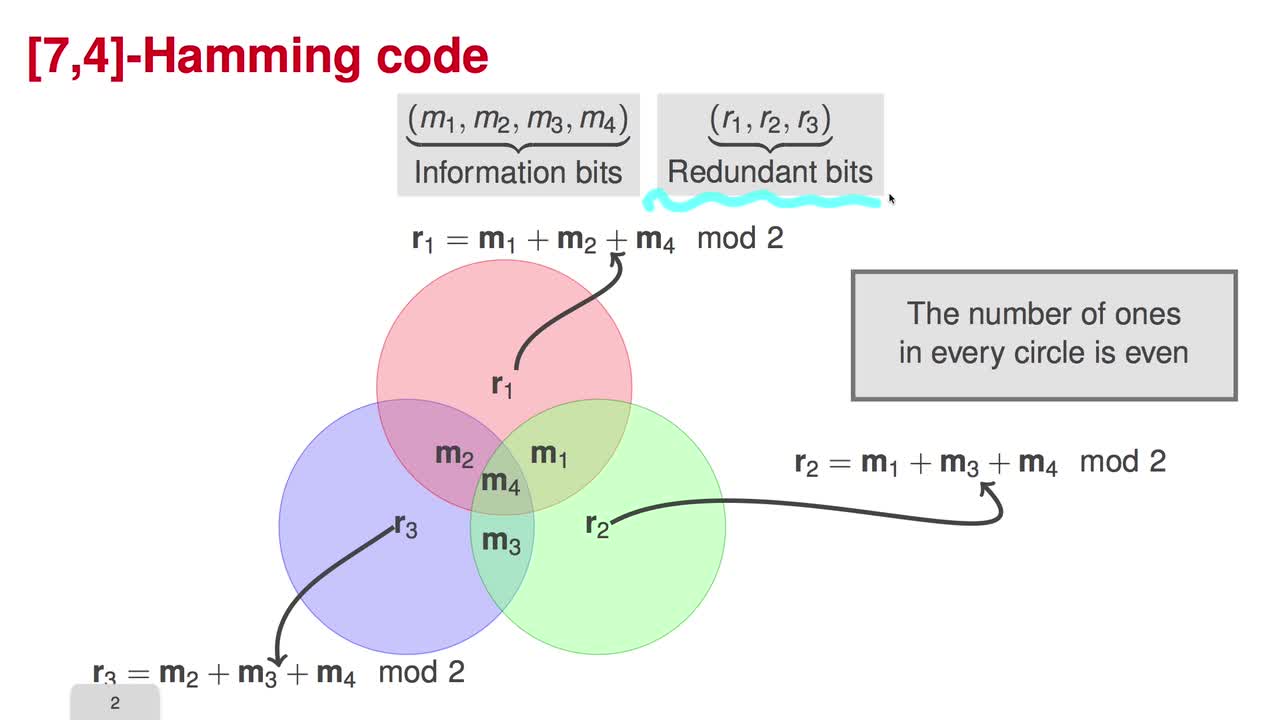
1.4. Parity Checking
There are two standard ways to describe a subspace, explicitly by giving a basis, or implicitly, by the solution space of the set of homogeneous linear equations. Therefore, there are two ways of
1.5. Error Correcting Capacity
This sequence will be about the error-correcting capacity of a linear code. We describe the way of considering the space Fq^n as a metric space. This metric is necessary to justify the principle of
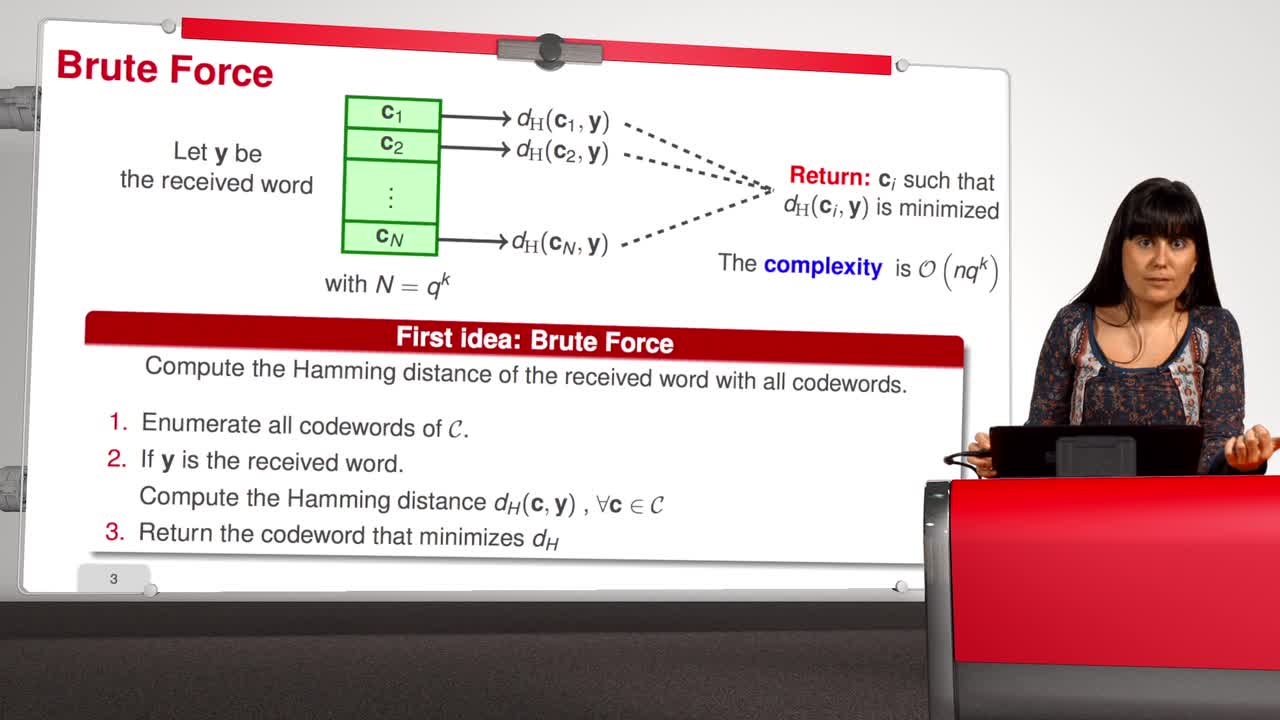
1.6. Decoding (A Difficult Problem)
The process of correcting errors and obtaining back the message is called decoding. In this sequence, we will focus on this process, the decoding. We would like that the decoder of the received
1.7. Reed-Solomon Codes
Reed-Solomon codes were introduced by Reed and Solomon in the 1960s. These codes are still used in storage device, from compact-disc player to deep-space application. And they are widely used
1.8. Goppa Codes
In this session, we will talk about another family of codes that have an efficient decoding algorithm: the Goppa codes. One limitation of the generalized Reed-Solomon codes is the fact that the
1.9. McEliece Cryptosystem
This is the last session of the first week of this MOOC. We have already all the ingredients to talk about code-based cryptography. Recall that in 1976 Diffie and Hellman published their famous
Intervenants et intervenantes
Auteur d'une thèse en mathématiques et informatique à l'Ecole polytechnique de Paris
Chercheuse à la faculté des sciences de l'université de La Laguna. Spécialités : code, cryptograhie et algèbre informatique (2015)
Enseignant chercheur en informatique à l'INRIA. Thèmes de recherche : Codes correcteurs d'erreurs et Cryptographie.