Notice
Cryptographie - partie 5 : arithmétique pour RSA
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
Chapitre "Cryptographie" - Partie 5 : L'arithmétique pour RSA
Plan : Le petit théorème de Fermat amélioré ; L'algorithme d'Euclide étendu ;
Inverse modulo n ; L'exponentiation rapide
Exo7. Cours et exercices de mathématiques pour les étudiants.
Retrouvez le polycopié sur http://exo7.emath.fr
Intervention
Thème
Dans la même collection
-
Cryptographie - partie 1 : chiffrement de César
BODIN Arnaud
Chapitre "Cryptographie" - Partie 1 : Le chiffrement de César Plan : César a dit... ; Des chiffres et des lettres ; Modulo ; Chiffrer et déchiffrer ; Espace des clés et attaque ; Algorithmes Exo7.
-
Cryptographie - partie 6 : chiffrement RSA
BODIN Arnaud
RECHER François
Chapitre "Cryptographie" - Partie 6 : Le chiffrement RSA Plan : Calcul de la clé publique et de la clé privée ; Chiffrement du message ; Déchiffrement du message ; Algorithmes Exo7. Cours et
-
Cryptographie - partie 2 : chiffrement de Vigenère
BODIN Arnaud
RECHER François
Chapitre "Cryptographie" - Partie 2 : Le chiffrement de Vigenère Plan : Chiffrement mono-alphabétique ; Le chiffrement de Vigenère ; Algorithmes Exo7. Cours et exercices de mathématiques pour les
-
Cryptographie - partie 4 : cryptographie à clé publique
BODIN Arnaud
RECHER François
Chapitre "Cryptographie" - Partie 4 : La cryptographie à clé publique Plan : Le principe de Kerckhoffs ; Fonctions à sens unique ; Chiffrement à clé publique Exo7. Cours et exercices de
-
Cryptographie - partie 3 : la machine Enigma et les clés secrètes
BODIN Arnaud
RECHER François
Chapitre "Cryptographie" - Partie 3 : La machine Enigma et les clés secrètes Plan : Un secret parfait ; La machine Enigma ; Des zéros et des uns ; La ronde des chiffres : DES Exo7. Cours et
Avec les mêmes intervenants et intervenantes
-
Exercice 6 (Courbes planes) [06986]
BODIN Arnaud
BLANC-CENTI Léa
Point singulier et allure de la courbe. Bonus (à 17'42'') : Les différentes types de points singuliers. Exo7. Cours et exercices de mathématiques pour les étudiants. Retrouvez la correction écrite
-
Exercice 4 (Equations différentielles) [06994]
BODIN Arnaud
BLANC-CENTI Léa
Résolution d'équations différentielles avec recherche d'une solution particulière par la méthode de variation de la constante. Bonus (à 22'15'') : Méthode de variation de la constante. Exo7. Cours
-
Exercice 13 (Equations différentielles) [07003]
BODIN Arnaud
BLANC-CENTI Léa
Exercice 13 (Equations différentielles) [07003] Fonctions vérifiant f'(x) = f(1/x). Bonus (à 17'26'') : Equation du pendule. Exo7. Cours et exercices de mathématiques pour les étudiants. Retrouvez
-
Exercice 1 (Courbes planes) [06981]
BODIN Arnaud
BLANC-CENTI Léa
Graphe d'une fonction, tangente, position par rapport à cette tangente. Bonus (à 26'17'') : Dominae d'atude, tangente par les DL, asymptote pour les graphes de fonctions. Exo7. Cours et exercices de
-
Exercice 9 (Courbes planes) [06989]
BODIN Arnaud
BLANC-CENTI Léa
Etude de trois courbes en coordonnées polaires (dont la cissoïde et une lemniscate). Bonus (à 28'12'') : Coordonnées polaires. Exo7. Cours et exercices de mathématiques pour les étudiants.
-
Exercice 7 (Equations différentielles) [06997]
BODIN Arnaud
BLANC-CENTI Léa
Equations différentielles linéaires du second ordre. Bonus (à 10'52'') : Rappels de cours. Exo7. Cours et exercices de mathématiques pour les étudiants. Retrouvez la correction écrite sur http:/
-
Exercice 4 (Courbes planes) [06984]
BODIN Arnaud
BLANC-CENTI Léa
Domaine d'étude et tracé d'une courbe paramétrée. Bonus (à 12'51'') : Recherche des symétries. Exo7. Cours et exercices de mathématiques pour les étudiants. Retrouvez la correction écrite sur http:
-
Exercice 2 (Equations différentielles) [06992]
BODIN Arnaud
BLANC-CENTI Léa
Fonctions vérifiant f'(x)+f(x) = f(0)+f(1). Bonus (à 5'11'') : Fonctions vérifiant f(x+t) = f(x).f(t). Exo7. Cours et exercices de mathématiques pour les étudiants. Retrouvez la correction écrite
-
Exercice 10 (Equations différentielles) [07000]
BODIN Arnaud
BLANC-CENTI Léa
Equations différentielles du second ordre résolues par changement de variables. Bonus (à 16'00'') : Autre méthode pour résoudre l'exercice. Exo7. Cours et exercices de mathématiques pour les
-
Exercice 7 (Courbes planes) [06987]
BODIN Arnaud
BLANC-CENTI Léa
Etude complète d'une courbe : variations conjointes, tangentes, asymptotes, points singuliers, tracé. Bonus (à 24'02'') : Asymptote. Exo7. Cours et exercices de mathématiques pour les étudiants.
-
Exercice 5 (Equations différentielles) [06995]
BODIN Arnaud
BLANC-CENTI Léa
Résolutions d'équations différentielles à variables séparées. Bonus (à 16'53'') : Equation à variables séparées. Exo7. Cours et exercices de mathématiques pour les étudiants. Retrouvez la
-
Exercice 2 (Courbes planes) [06982]
BODIN Arnaud
BLANC-CENTI Léa
Courbes paramétrées et graphes de fonctions. Bonus (à 10'00'') : Paramétrisation d'un graphe. Exo7. Cours et exercices de mathématiques pour les étudiants. Retrouvez la correction écrite sur http:/
![Exercice 6 (Courbes planes) [06986]](https://vod.canal-u.tv/videos/media/images/tele2sciences/exercice.6.courbes.planes.06986._18644/vignette.exo7.png)
![Exercice 4 (Equations différentielles) [06994]](https://vod.canal-u.tv/videos/media/images/tele2sciences/exercice.4.equations.diff.rentielles.06994._18652/vignette.exo7.png)
![Exercice 13 (Equations différentielles) [07003]](https://vod.canal-u.tv/videos/media/images/tele2sciences/exercice.13.equations.diff.rentielles.07003._18661/vignette.exo7.png)
![Exercice 1 (Courbes planes) [06981]](https://vod.canal-u.tv/videos/media/images/tele2sciences/exercice.1.courbes.planes.06981._18639/vignette.exo7.png)
![Exercice 9 (Courbes planes) [06989]](https://vod.canal-u.tv/videos/media/images/tele2sciences/exercice.9.courbes.planes.06989._18647/vignette.exo7.png)
![Exercice 7 (Equations différentielles) [06997]](https://vod.canal-u.tv/videos/media/images/tele2sciences/exercice.7.equations.diff.rentielles.06997._18655/vignette.exo7.png)
![Exercice 4 (Courbes planes) [06984]](https://vod.canal-u.tv/videos/media/images/tele2sciences/exercice.4.courbes.planes.06984._18642/vignette.exo7.png)
![Exercice 2 (Equations différentielles) [06992]](https://vod.canal-u.tv/videos/media/images/tele2sciences/exercice.2.equations.diff.rentielles.06992._18650/vignette.exo7.png)
![Exercice 10 (Equations différentielles) [07000]](https://vod.canal-u.tv/videos/media/images/tele2sciences/exercice.10.equations.diff.rentielles.07000._18658/vignette.exo7.png)
![Exercice 7 (Courbes planes) [06987]](https://vod.canal-u.tv/videos/media/images/tele2sciences/exercice.7.courbes.planes.06987._18645/vignette.exo7.png)
![Exercice 5 (Equations différentielles) [06995]](https://vod.canal-u.tv/videos/media/images/tele2sciences/exercice.5.equations.diff.rentielles.06995._18653/vignette.exo7.png)
![Exercice 2 (Courbes planes) [06982]](https://vod.canal-u.tv/videos/media/images/tele2sciences/exercice.2.courbes.planes.06982._18640/vignette.exo7.png)
Sur le même thème
-
Quel est le prix à payer pour la sécurité de nos données ?
MINAUD Brice
À l'ère du tout connecté, la question de la sécurité de nos données personnelles est devenue primordiale. Comment faire pour garder le contrôle de nos données ? Comment déjouer les pièges de plus en
-
Des systèmes de numération pour le calcul modulaire
BAJARD Jean-Claude
Le calcul modulaire est utilisé dans de nombreuses applications des mathématiques, telles que la cryptographie. La réduction modulaire dans un contexte très général est coûteuse, car elle n
-
Inauguration de l'exposition - Vanessa Vitse : Nombres de Sophie Germain et codes secrets
VITSE Vanessa
Exposé de Vanessa Vitse (Institut Fourier) : Nombres de Sophie Germain et codes secrets
-
Information Structures for Privacy and Fairness
PALAMIDESSI Catuscia
Information Structures for Privacy and Fairness
-
AI and Human Decision-Making: An Interdisciplinary Perspective
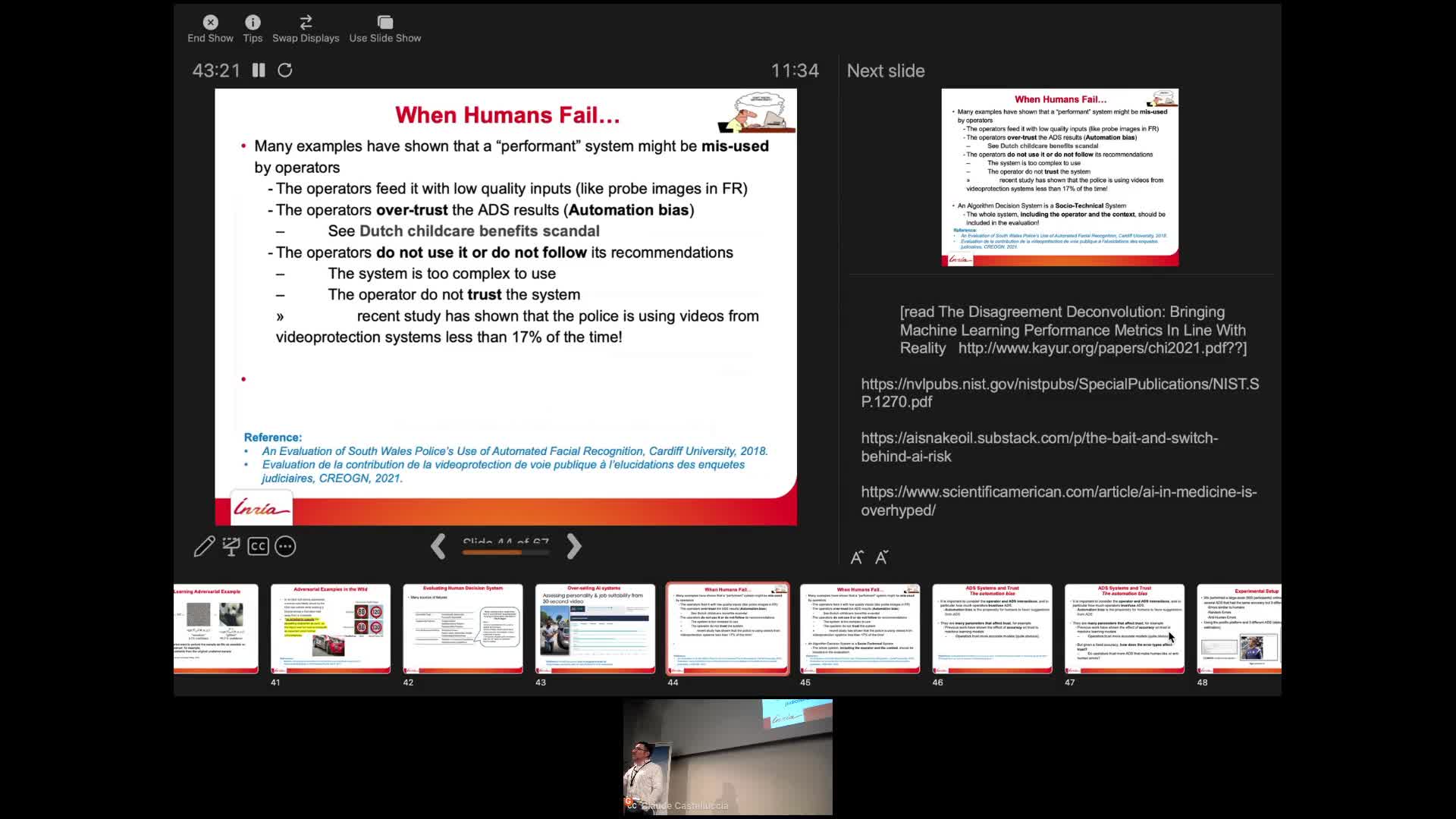
CASTELLUCCIA Claude
This seminar will talk about some of the privacy risks of these systems and will describe some recent attacks. It will also discuss why they sometimes fail to deliver. Finally, we will also show that
-
4.7. Attack against Reed-Muller codes
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In this session, we will introduce an attack against binary Reed-Muller codes. Reed-Muller codes were introduced by Muller in 1954 and, later, Reed provided the first efficient decoding algorithm
-
5.6. An Efficient Provably Secure One-Way Function
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In this session, we are going to see how to build an efficient provably secure one-way function from coding theory. As you know, a one-way function is a function which is simple to evaluate and
-
5.1. Code-Based Digital Signatures
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
Welcome to the last week of this MOOC on code-based cryptography. This week, we will be discussing other cryptographic constructions relying on coding theory. We have seen how to do public key
-
4.5. Error-Correcting Pairs
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
We present in this session a general decoding method for linear codes. And we will see it in an example. Let C be a generalized Reed-Solomon code of dimension k associated to the pair (c, d). Then,
-
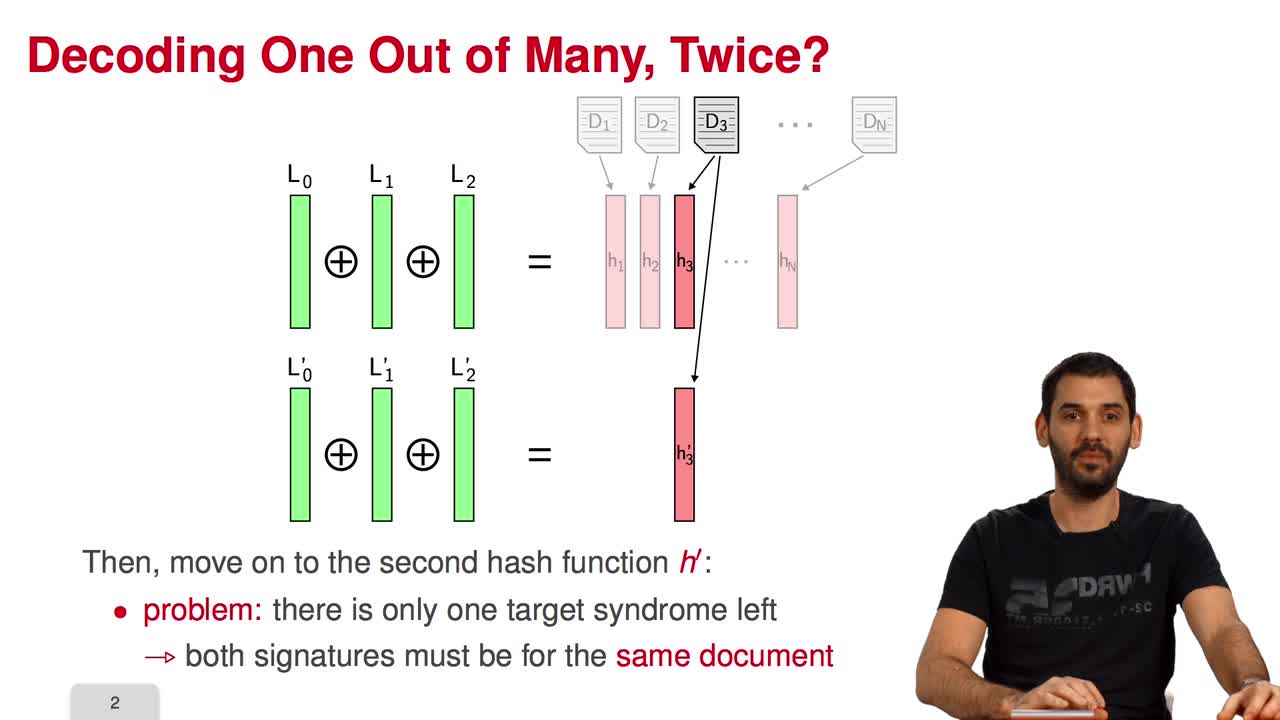
5.4. Parallel-CFS
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In this session, I will present a variant of the CFS signature scheme called parallel-CFS. We start from a simple question: what happens if you try to use two different hash functions and compute
-
4.8. Attack against Algebraic Geometry codes
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In this session, we will present an attack against Algebraic Geometry codes (AG codes). Algebraic Geometry codes is determined by a triple. First of all, an algebraic curve of genus g, then a n
-
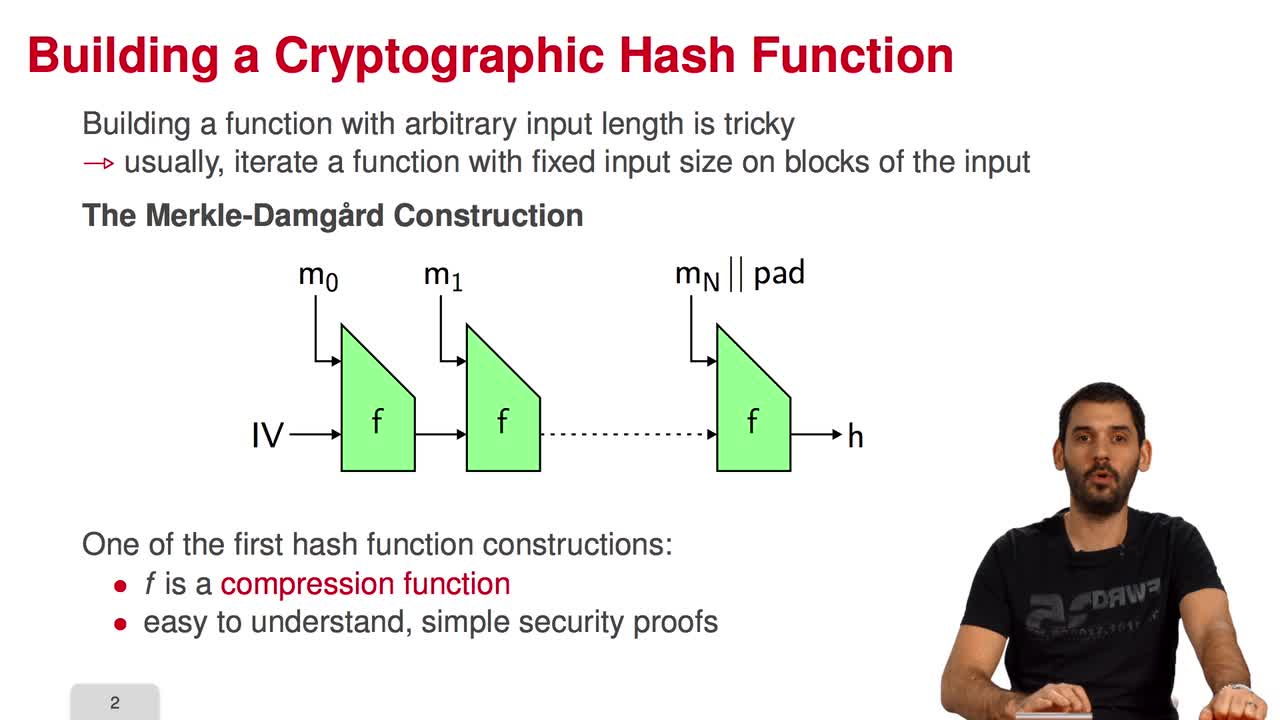
5.7. The Fast Syndrome-Based (FSB) Hash Function
MARQUEZ-CORBELLA Irene
SENDRIER Nicolas
FINIASZ Matthieu
In the last session of this week, we will have a look at the FSB Hash Function which is built using the one-way function we saw in the previous session. What are the requirements for a
