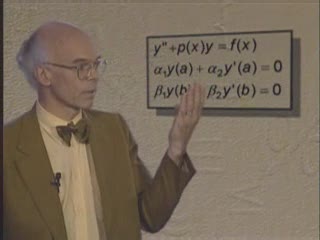Chapitres
- Introduction et exercice 108'03"
- Exercice 2 et sa résolution09'41"
- Synthèse sur les exercices et concept fondamental06'23"
- Le théorème central10'59"
- La deuxième formule10'11"
- La troisième formule06'12"
- Conclusion02'46"
Notice
Les espaces de Hilbert et les opérateurs compacts
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
Calcul différentiel et calcul intégral sont deux sous-ensembles fondamentaux du cours de mathématiques du second cycle. Ce vidéocours propose une série de "zooms" transversaux qui permettent de faire une synthèse de connaissances et de vérifier les concepts fondamentaux.
VIDÉOCOURS DE MATHÉMATIQUES LICENCE
NIVEAU : Supérieur / Licence
DURÉE : 10 x 26 mn et 5 x 52 mn
ANNÉE : 2000
Auteur(s) / Responsable(s) scientifiques(s) : Jacques Vauthier, Université Paris 6 Réalisateur(s) : Dominique Morque Producteur(s) : Université Nancy 2 / Vidéoscop
Les vidéocours de MATHÉMATIQUES LICENCE portent sur les CALCUL DIFFÉRENTIEL ET CALCUL INTÉGRAL. Calcul différentiel et calcul intégral sont deux sous-ensembles fondamentaux du cours de mathématiques du second cycle. Ce vidéocours propose une série de "zooms" transversaux qui permettent aux étudiants de faire une synthèse de leurs connaissances et de vérifier qu'ils ont acquis les concepts fondamentaux.
N°1 : Généralités (26 min.) Les formules de Taylor (26 min.)
N°2 : Les grands théorèmes (26 min.) Les extrema (26 min.)
N°4 : Les équations différentielles linéaires (52 min.)
N°5 : Les équations différentielles linéaires dans le champ complexe
N°6 : Les théorèmes de convergence monotone et de convergence dominée de Lebesgue (52 min.)
N°7 : Les différents types de convergence (26 min.) Le théorème de Radon-Nicodym (26 min.)
N°8 : La transformation de Fourier (52 min.)
N°9 : Le théorème de Baire et sa descendance (52 min.)
N°10 : Les espaces de Hilbert et les opérateurs compacts (52 min.)
GénériqueLICENCE DE MATHÉMATIQUES, CALCUL DIFFÉRENTIEL Émission conçue et préparée par Jacques VAUTHIER Centre de Télé-enseignement Universitaire Université Pierre et Marie Curie - Paris 6 Émission réalisée avec le soutien du Ministère de l'Education Nationale de la Recherche et des Technologies - DT Production déléguée et exécutive Université Nancy 2 - VIDEOSCOP Directeur de production Philippe Perrey Réalisation Dominique Morque Prise de son Thierry Hurault Cadre Franck Infelta Maquillage Jocelyne Schwartz Suivi de production Agnès Divoux Étudiante Priscille Remerciements particuliers à Françoise Thibault © Université Nancy 2 - 1999
Intervention / Responsable scientifique
Dans la même collection
-
Le problème de Sturm-Liouville
VauthierJacquesCalcul différentiel et calcul intégral sont deux sous-ensembles fondamentaux du cours de mathématiques du second cycle. Ce vidéocours propose une série de "zooms" transversaux qui permettent de faire
-
Les extrema
VauthierJacquesCalcul différentiel et calcul intégral sont deux sous-ensembles fondamentaux du cours de mathématiques du second cycle. Ce vidéocours propose une série de "zooms" transversaux qui permettent de faire
-
La transformation de Fourier
VauthierJacquesCalcul différentiel et calcul intégral sont deux sous-ensembles fondamentaux du cours de mathématiques du second cycle. Ce vidéocours propose une série de "zooms" transversaux qui permettent de faire
-
Les équations différentielles linéaires
VauthierJacquesCalcul différentiel et calcul intégral sont deux sous-ensembles fondamentaux du cours de mathématiques du second cycle. Ce vidéocours propose une série de "zooms" transversaux qui permettent de faire
-
Les différents types de convergence
VauthierJacquesCalcul différentiel et calcul intégral sont deux sous-ensembles fondamentaux du cours de mathématiques du second cycle. Ce vidéocours propose une série de "zooms" transversaux qui permettent de faire
-
Calcul différentiel : généralités
VauthierJacquesCalcul différentiel et calcul intégral sont deux sous-ensembles fondamentaux du cours de mathématiques du second cycle. Ce vidéocours propose une série de "zooms" transversaux qui permettent de faire
-
Les théorèmes de convergence monotone et de convergence dominée de Lebesgue
VauthierJacquesCalcul différentiel et calcul intégral sont deux sous-ensembles fondamentaux du cours de mathématiques du second cycle. Ce vidéocours propose une série de "zooms" transversaux qui permettent de faire
-
Le théorème de Radon-Nicodym
VauthierJacquesCalcul différentiel et calcul intégral sont deux sous-ensembles fondamentaux du cours de mathématiques du second cycle. Ce vidéocours propose une série de "zooms" transversaux qui permettent de faire
-
Les grands théorèmes - calcul différentiel
VauthierJacquesCalcul différentiel et calcul intégral sont deux sous-ensembles fondamentaux du cours de mathématiques du second cycle. Ce vidéocours propose une série de "zooms" transversaux qui permettent de faire
-
Le théorème de Fubini et sa convolution
VauthierJacquesCalcul différentiel et calcul intégral sont deux sous-ensembles fondamentaux du cours de mathématiques du second cycle. Ce vidéocours propose une série de "zooms" transversaux qui permettent de faire
-
Les formules de Taylor
VauthierJacquesCalcul différentiel et calcul intégral sont deux sous-ensembles fondamentaux du cours de mathématiques du second cycle. Ce vidéocours propose une série de "zooms" transversaux qui permettent de faire
-
Les équations différentielles linéaires dans le champ complexe
VauthierJacquesCalcul différentiel et calcul intégral sont deux sous-ensembles fondamentaux du cours de mathématiques du second cycle. Ce vidéocours propose une série de "zooms" transversaux qui permettent de faire
Avec les mêmes intervenants et intervenantes
-
Nombres réels
VauthierJacquesCe vidéocours de Mathématiques première année est conçu comme un complément de cours destiné aux étudiants abordant les études universitaires pour la première fois. Ce public a tout particulièrement
-
Le temps
JullienFrançoisDagognetFrançoisHeinzmannGerhardWalterScottNabonnandPhilippeBriandJean-PierreSolerLénaVauthierJacquesMorangeMichelJean-Pierre Briand, physicien des particules élémentaires et François Jullien, philosophe, évoquent, l'un et l'autre leur conception de la notion de temps. Aristote, Platon, Saint-Augustin, Thomas d
-
Le monde est-il mathématique ?
JullienFrançoisDagognetFrançoisHeinzmannGerhardWalterScottNabonnandPhilippeBriandJean-PierreSolerLénaMorangeMichelVauthierJacquesÀ travers des séquences de commentaires de texte, allant de Platon à Poincaré, en passant par Galilée ou Hume, nous découvrons comment, tout au long de l'histoire, les plus grands esprits et les
-
Espaces Vectoriels - Applications linéaires
VéluJacquesVauthierJacquesCe vidéocours de Mathématiques première année est conçu comme un complément de cours destiné aux étudiants abordant les études universitaires pour la première fois. Ce public a tout particulièrement
-
Développements asymptotiques
VauthierJacquesCe vidéocours de Mathématiques première année est conçu comme un complément de cours destiné aux étudiants abordant les études universitaires pour la première fois. Ce public a tout particulièrement
-
La science pense-t-elle ?
JullienFrançoisDagognetFrançoisHeinzmannGerhardWalterScottNabonnandPhilippeBriandJean-PierreSolerLénaMorangeMichelVauthierJacquesLorsque Heideger écrit en 1954 : " La science ne pense pas ", il parle en tant que métaphysicien. Sortie de son contexte, cette formule a connu la postérité et est alors devenue très provocatrice.
-
Suites et continuité
VauthierJacquesCe vidéocours de Mathématiques première année est conçu comme un complément de cours destiné aux étudiants abordant les études universitaires pour la première fois. Ce public a tout particulièrement
-
Déterminants, diagonalisation des matrices
VéluJacquesVauthierJacquesCe vidéocours de Mathématiques première année est conçu comme un complément de cours destiné aux étudiants abordant les études universitaires pour la première fois. Ce public a tout particulièrement
-
Les sciences de l'esprit
JullienFrançoisDagognetFrançoisHeinzmannGerhardWalterScottNabonnandPhilippeBriandJean-PierreSolerLénaVauthierJacquesMorangeMichelQue signifie percevoir, reconnaître un visage, manier le langage, être conscient, penser, ressentir une émotion ? Ces interrogations autrefois littéraires et philosophiques sont devenues récemment
-
Le vivant
JullienFrançoisDagognetFrançoisHeinzmannGerhardWalterScottNabonnandPhilippeBriandJean-PierreSolerLénaVauthierJacquesMorangeMichelMichel Morange, qui dirige un important laboratoire de biologie moléculaire à l'École Normale Supérieure, définit ce qu'il faut entendre par "vivant", brosse les grandes lignes du consensus actuel sur
-
Systèmes linéaires et matrices
VéluJacquesVauthierJacquesCe vidéocours de Mathématiques première année est conçu comme un complément de cours destiné aux étudiants abordant les études universitaires pour la première fois. Ce public a tout particulièrement
-
Nombres complexes - Fractions rationnelles
VéluJacquesVauthierJacquesCe vidéocours de Mathématiques première année est conçu comme un complément de cours destiné aux étudiants abordant les études universitaires pour la première fois. Ce public a tout particulièrement
Sur le même thème
-
« Traitement et analyse des données au sein d'une chaîne éditoriale » (mars 2022)
PorteGuillaumeHeidenSergePrésentées conjointement, ces deux briques de la chaîne sont en effet intimement liées. Via la présentation de certains outils, nous verrons comment l’enrichissement d’un document numérique à l’aide
-
Initiation à l’analyse de réseaux
Ruiz FaboPabloLes réseaux constituent une structure pratique pour représenter des données relationnelles de façon à donner un aperçu de groupes et interactions.
-
Simuler pour optimiser : introduction
CherouatAbelL’objectif de ce vidéocours est de vous initier au potentiel de la modélisation expérimentale ou numérique dans l’optimisation des systèmes, procédés de fabrication, organisation d’une chaine de
-
Simuler pour optimiser : conclusion
CherouatAbelL’objectif de ce vidéocours a été de vous initier au potentiel de la modélisation expérimentale ou numérique dans l’optimisation des systèmes, procédés de fabrication, organisation d’une chaine de
-
Cherif HANNA : Se perdre pour mieux se retrouver, une expérience pédagogique de projétation archite…
Cherif HANNA : Se perdre pour mieux se retrouver, une expérience pédagogique de projétation architecturale hors de l'urbain
-
AKP'nin 2009 yerel seçimlerinde alacağı sonuçlar hangi kıstaslara göre değerlendirilmeli ?
ÇakırRuşenRuşen Çakır AKP'nin 2009 yerel seçimlerinde alacağı sonuçlar hangi kıstaslara göre değerlendirilmeli ? Les élections municipales du 29 mars 2009
-
Repenser la mobilité sociale - Rémi Sinthon
SinthonRémiComment décrire la place de chacun dans une société ? Comment rendre compte de la position sociale atteinte par un individu, par une famille ou par un groupe ?
-
Hajar Bahouri - De l'analyse des EDPs non linéaires à la théorie des groupes
Créteil, Prix Paul Doisteau 2016 Réalisation technique : Antoine Orlandi (GRICAD) | Tous droits réservés
-
La fonction RH à l’ère du digital
MercierEstelleA travers l'exemple d'entreprises basées en Lorraine, La fonction RH à l'ère du digital dresse un état des lieux des opportunités et des risques liés aux nouveaux usages du numérique
-
Anthropologies of dialogue 2015 : Closing conference - Dialogic Ethics : A Pragmatic Hope for this …
ArnettRonald CColloque international "Anthropologies of dialogue", les 27-29 août 2015 au campus Lettres et et Sciences humaines à Nancy Saturday 29th August Morning Plenary Session : Closing conference -
-
Anthropologies of dialogue 2015 : The dialogical form of the communication
TrognonAlainColloque international "Anthropologies of dialogue", les 27-29 août 2015 au campus Lettres et et Sciences humaines à Nancy Thursday 27th August Morning Plenary Session. The dialogical
-
Anthropologies of dialogue 2015 : Dialogue and Rationality
VandervekenDanielColloque international "Anthropologies of dialogue", les 27-29 août 2015 au campus Lettres et et Sciences humaines à Nancy Friday 28th August Morning Plenary Session - Dialogue and