Chapitres
- Introduction02'08"
- René Thom02'48"
- Des langages pour un univers en caoutchouc01'39"
- - Topologie01'26"
- - Mesure d'un objet dans un espace01'40"
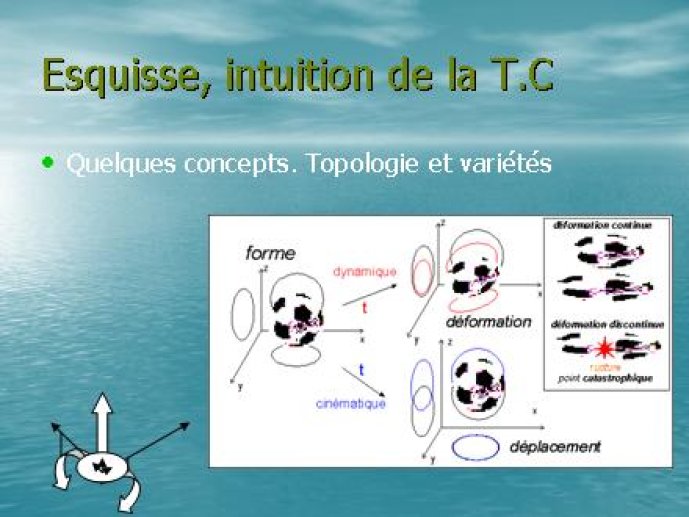
- * Différents modèles01'44"
- * Peigner un hérisson 01'32"
- - Caractéristique d'Euler-Poincaré01'54"
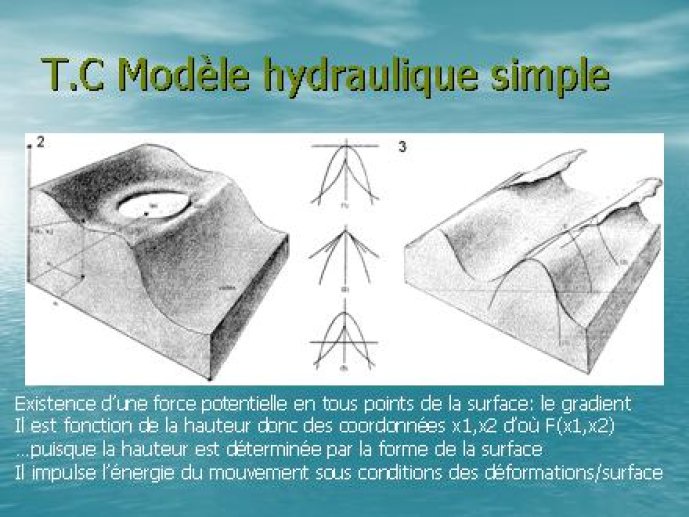
- - Le modèle hydraulique01'40"
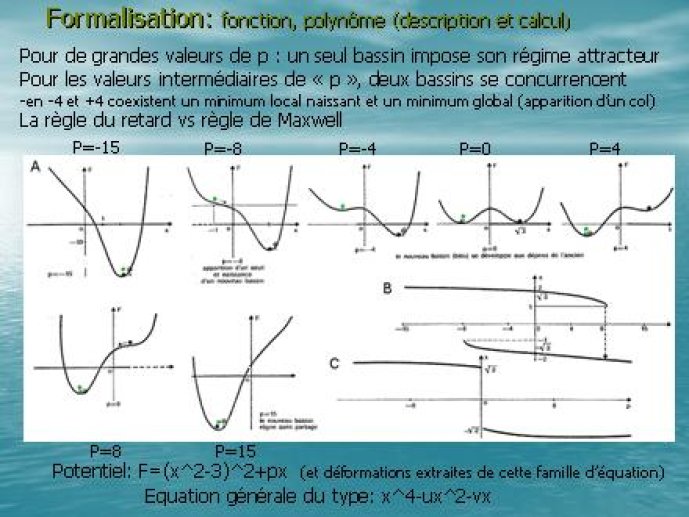
- - Formalisation04'14"
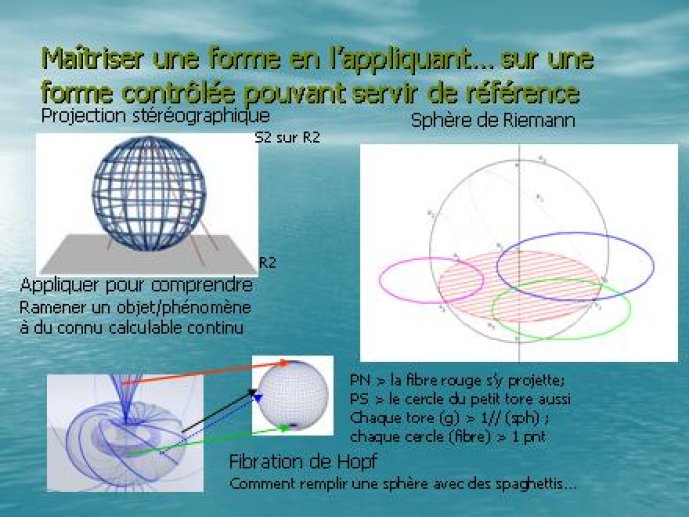
- - Géométrisation02'41"
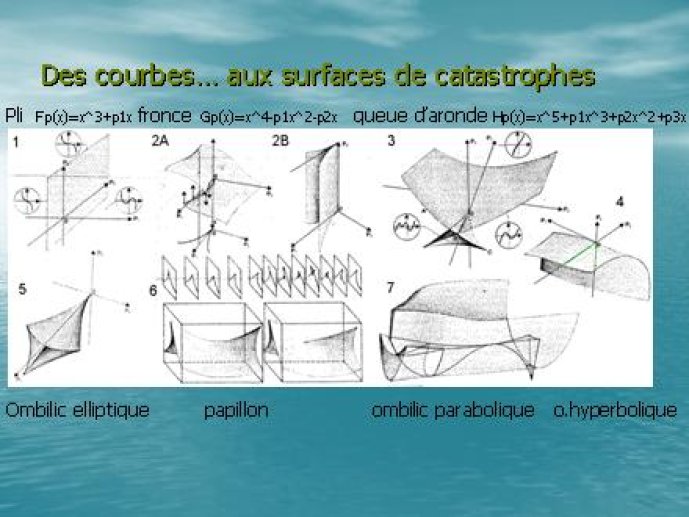
- - Courbes de catastrophes00'53"
- - Surfaces de catastrophes02'56"
- - Les 7 catastrophes élémentaires00'42"
- Théorie des Catastrophes : définition00'44"
- Quelques applications01'29"
- - Optique géométrique, caustiques02'42"
- - Lentilles gravitationnelles02'19"
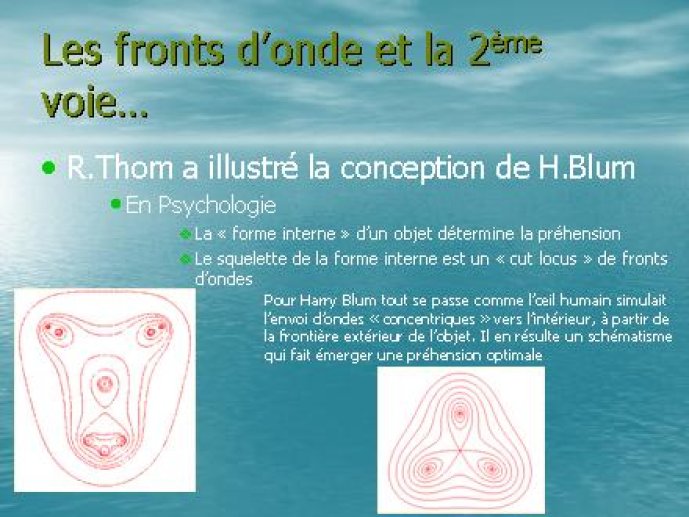
- - Deuxième voie en Psychologie02'04"
- - Deuxième voie en Ethologie01'51"
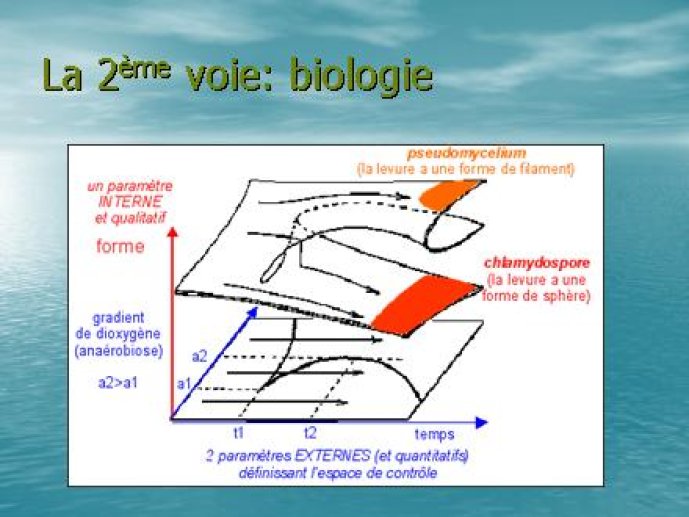
- - Deuxième voie en Biologie01'36"
- - Herméneutique et boîte noire03'08"
- Quels espoirs ? Pour qui ? Pour quoi ?03'06"
- Une voie moyenne exigeante06'19"
- Une voie moyenne humble05'57"
- Espoir sur la Théorie des Catastrophes02'30"
- L'Institut des Hautes Etudes Scientifiques04'12"
Notice
Espoir et théorie des catastrophes. L’intelligibilité : norme d’une science de l’acceptable ?
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
Fondée dans les années 70 par le mathématicien René Thom, la théorie des catastrophes devient rapidement, malgré l’engouement qu’elle suscite, sujet de controverse et de critique. Visant à décrire les phénomènes discontinus à l'aide de modèles mathématiques continus, elle se définit comme un langage mathématique, un outil d’intelligibilité du monde mais son manque de rigueur et sa nature qualitative laissent sceptique positivistes et mathématiciens purs.
Bien que ces critiques n’aient que partiellement entamé son expansion puisque ses domaines d’application s’étendent au fil du temps de la biologie aux disciplines de sciences humaines telles que l’éthologie et la psychologie (théorie de Harry Blum), elles sont à l’origine du désintérêt des chercheurs pour ce langage mathématique apte selon Luc Gootjes à relever de nouveaux défis scientifiques.
La conférence a été donnée à l'Université Victor Segalen Bordeaux 2 dans le cadre du cycle de conférences "L'invité du Mercredi" / Saison 2005-2006 sur le thème "L'espoir". Service culturel Université Victor Segalen de Bordeaux 2 / DCAM /
Thème
Documentation
Liens
Institut des Hautes Etudes Scientifiques
Les modèles morpho-dynamiques en sciences cognitives et sciences humaines - Jean PetitotArchives Audiovisuelles de la Recherche
Dans la même collection
-
Espoir et Histoire
Riot-SarceyMichèleLes mouvements de révolte qui secouent actuellement notre société sont symptomatiques d'une crise du jeu démocratique. La représentation politique ne fonctionne pas comme elle le devrait puisqu'il est
-
L’espoir à l’épreuve du progrès
CoiffetJean-ClaudeComment aider l’homme à sortir de la désespérance où le plonge l’angoisse existentielle de nos sociétés modernes individualistes ? Par l’espoir ou par le progrès, deux réponses distinctes, pour ne pas
-
La Cité Idéale dans l’ancien stoïcisme : un espoir, un mythe ?
CambronnePatriceLe stoïcisme apparaît au début de l'époque hellénistique, à un moment où les Grecs, démoralisés, voient s'effondrer leur civilisation et avec elle les valeurs de la cité. En quête d’un Etat porteur
-
Les théorèmes de Gödel : fin d’un espoir ?
DeshouillersJean-MarcEn 1931, Kurt Gödel (1906 - 1978) démontrait, dans un article révolutionnaire, qu'un système d'axiomes cohérent et suffisamment expressif est susceptible de générer des énoncés dont la validité ne
-
Des biopuces et des hommes
GidrolXavierConférence du docteur Xavier Gidrol sur l'impact des nanotechnologies en médecine. La conférence a été donnée à l'Université Victor Segalen Bordeaux 2 dans le cadre du cycle de conférences "L'invité
-
Bases naturelles de l'Espoir : cognition et/ou motivation
BioulacBernardEn biologie, le mot espoir est rarement utilisé. Aristote est le père du naturalisme. Hippocrate fut le premier à parler de la maladie de la perte de l'espoir, il mit au point la théorie des humeurs.
-
Une nouvelle théorie du cancer
KupiecJean-JacquesConférence publique proposant une vision darwinienne des processus de différenciation cellulaire pouvant rendre compte du phénomène de tumorisation.
Sur le même thème
-
Clinique de la rue : de l’abriter à l’habiter.
VinotFrédéricProjet soutenu par la MSHS Sud-Est, il émane plus particulièrement de l’axe 1 du LAPCOS « Territoires et environnements : approches plurivoques de l'habiter ». Dans le cadre de l'axe 4 de la MSHS Sud
-
Cartographies et topologies artistiques
LefrançoisFrédéricRavion-D'IngianniSophieMusquerStanLucolFélie-LineJournée d’études coordonnée par Frédéric Lefrançois, le 18 décembre 2017, à l'Amphi Recherche du Campus de Fouillole (Université des Antilles)
-
Colonies spatiales et visions du futur. Vers une société de contrôle ?
JeanninHélèneSéminaires de master 2023 – 2024 – Anthropologie Fondamentale : aux limites de l’humain
-
Conquête spatiale et arts visuels : faire corps à corps avec le réel grâce au récit spéculatif
SophieDevauxSophie Devaux a saisi par l‘objectif les vestiges d’une aventure spatiale liée à la Guerre Froide comme un champ de ruines.
-
Affective atmospheres: place and memory on the early modern stage
TribbleEvelyn B.Talk by Evelyn TRIBBLE (Anglais, Connecticut), as part of the workshop "Memory, Place, and Material Culture", organized by John SUTTON, 2022-2023 research fellow at the Paris IAS, Emeritus Professor
-
The cognitive life of maps
CasatiRobertoTalk by Roberto CASATI (Philosophie, Institut Jean Nicod), as part of the workshop "Memory, Place, and Material Culture", organized by John SUTTON, 2022-2023 research fellow at the Paris IAS, Emeritus
-
2001 L’Odyssée de l’espace » (Stanley Kubrick, 1968), anthropologie et mythologie
CalvetYann2001 L’Odyssée de l’espace » (Stanley Kubrick, 1968), anthropologie et mythologie
-
Colonisation de l’espace : les stations orbitales sont-elles la solution aux problèmes terrestres ?
LehoucqRolandL’ESPACE : NOUVELLE FRONTIÈRE ? NOUVEL HORIZON
-
Exposition au Mucem : Connectivités
Morel-DeledalleMyriameMyriame Morel-Deledalle, Conservateur en chef du patrimoine au Musée des civilisations de l’Europe et de la Méditerranée (Mucem) a été commissaire de plusieurs expositions notables du Mucem (Volubilis
-
"Le mathématicien Petre (Pierre) Sergescu, historien des sciences, personnalité du XXe siècle"
HerléaAlexandreAlexandre HERLEA est membre de la section « Sciences, histoire des sciences et des techniques et archéologie industrielle » du CTHS. Professeur émérite des universités, membre effectif de l'Académie
-
Webinaire sur la rédaction des PGD
LouvetViolaineRédaction des Plans de Gestion de Données (PGD) sous l’angle des besoins de la communauté mathématique.
-
Alexandre Booms : « Usage de matériel pédagogique adapté en géométrie : une transposition à interro…
« Usage de matériel pédagogique adapté en géométrie : une transposition à interroger ». Alexandre Booms, doctorant (Université de Reims Champagne-Ardenne - Cérep UR 4692)
