Notice
Je suis Sophie Germain, femme et mathématicienne
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
Découvrez la vie de Sophie Germain (1776-1831) à travers ce film réalisé à l'occasion de la sortie de la bande-dessinée "Les Audaces de Sophie Germain" (E. Tartaglini - A. Fillipini - A. Ferrari, éditions Petit à petit, Docu-BD, 2021).
Retrouvez également ce film et des posters à travers l'exposition de l'institut Fourier, réalisée également à l'occasion de la sortie de la BD : https://sophiegermain20.sciencesconf.org/
Intervention / Responsable scientifique
Thème
Documentation
Dans la même collection
-
Inauguration de l'exposition - Hervé Pajot : Présentation
Présentation de l'exposition.
-
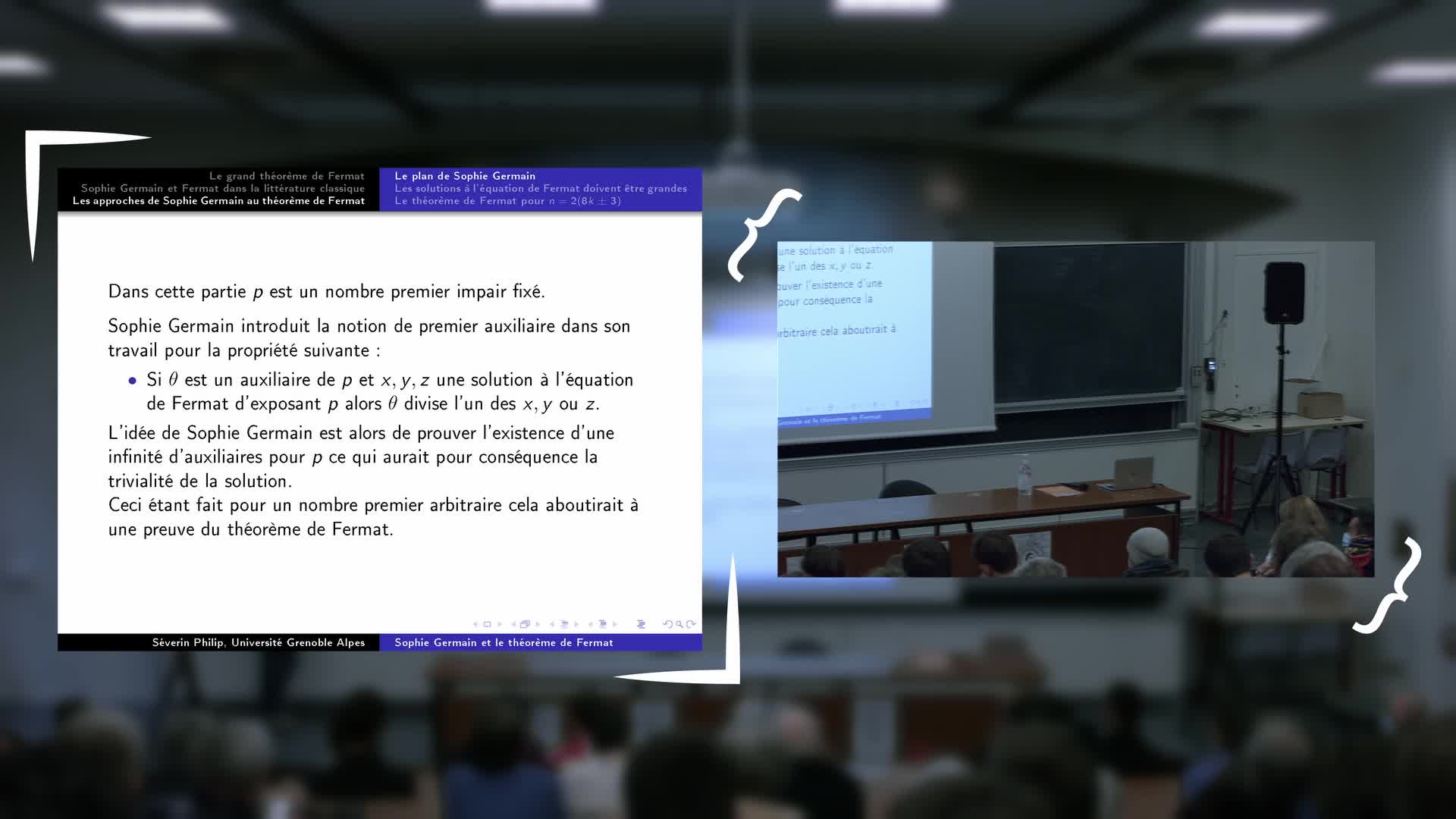
Inauguration de l'exposition - Séverin Philip : Sophie Germain et le théorème de Fermat
PhilipSéverinExposé de Severin Philip (Institut Fourier) : Sophie Germain et le théorème de Fermat
-
-
Inauguration de l'exposition - Clarisse Coulomb : Une scientifique au temps des Lumières
CoulombClarisseExposé de Clarisse Coulomb (Historienne, UGA) : Sophie Germain, une scientifique au temps des Lumières
-
Avec les mêmes intervenants et intervenantes
-
À la découverte de la vie de Joseph Fourier et de son oeuvre !
PajotHervéQuand un professeur de mathématiques raconte à sa fille...
Sur le même thème
-
Tuan Ta Pesao : écritures de sable et de ficelle à l'Ile d'Ambrym
VandendriesscheEricCe film se déroule au Nord de l’île d’Ambrym, dans l’archipel de Vanuatu, en Mélanésie...
-
"Le mathématicien Petre (Pierre) Sergescu, historien des sciences, personnalité du XXe siècle"
HerléaAlexandreAlexandre HERLEA est membre de la section « Sciences, histoire des sciences et des techniques et archéologie industrielle » du CTHS. Professeur émérite des universités, membre effectif de l'Académie
-
Webinaire sur la rédaction des PGD
LouvetViolaineRédaction des Plans de Gestion de Données (PGD) sous l’angle des besoins de la communauté mathématique.
-
Alexandre Booms : « Usage de matériel pédagogique adapté en géométrie : une transposition à interro…
« Usage de matériel pédagogique adapté en géométrie : une transposition à interroger ». Alexandre Booms, doctorant (Université de Reims Champagne-Ardenne - Cérep UR 4692)
-
M. Lesourd - Positive Scalar Curvature on Noncompact Manifolds and the Positive Mass Theorem
LesourdMartinThe study of positive scalar curvature on noncompact manifolds has seen significant progress in the last few years. A major role has been played by Gromov's results and conjectures, and in
-
R. Perales - Recent Intrinsic Flat Convergence Theorems
PeralesRaquelThéorèmes récents de convergence plane intrinsèque
-
J. Fine - Knots, minimal surfaces and J-holomorphic curves
FineJoëlI will describe work in progress, parts of which are joint with Marcelo Alves. Let L be a knot or link in the 3-sphere. I will explain how one can count minimal surfaces in hyperbolic 4-space
-
P. Burkhardt - Pointwise lower scalar curvature bounds for C0 metrics via regularizing Ricci flow
Burkhardt-GuimPaulaWe propose a class of local definitions of weak lower scalar curvature bounds that is well defined for C0 metrics. We show the following: that our definitions are stable under greater-than-second
-
D. Semola - Boundary regularity and stability under lower Ricci bounds
SemolaDanieleThe theory of non smooth spaces with lower Ricci Curvature bounds has undergone huge developments in the last thirty years. On the one hand the impetus came from Gromov’s precompactness theorem
-
D. Stern - Harmonic map methods in spectral geometry
SternDanielOver the last fifty years, the problem of finding sharp upper bounds for area-normalized Laplacian eigenvalues on closed surfaces has attracted the attention of many geometers, due in part to
-
Y. Lai - A family of 3d steady gradient Ricci solitons that are flying wings
LaiYiWe find a family of 3d steady gradient Ricci solitons that are flying wings. This verifies a conjecture by Hamilton. For a 3d flying wing, we show that the scalar curvature does not vanish at
-
R. Bamler - Compactness and partial regularity theory of Ricci flows in higher dimensions
BamlerRichard H.We present a new compactness theory of Ricci flows. This theory states that any sequence of Ricci flows that is pointed in an appropriate sense, subsequentially converges to a synthetic flow.