Notice
J. Fine - Knots, minimal surfaces and J-holomorphic curves
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
I will describe work in progress, parts of which are joint with Marcelo Alves. Let L be a knot or link in the 3-sphere. I will explain how one can count minimal surfaces in hyperbolic 4-space which have ideal boundary equal to L, and in this way obtain a knot invariant. In other words the number of minimal surfaces doesn’t depend on the isotopy class of the link. These counts of minimal surfaces can be organised into a two-variable polynomial which is perhaps a known polynomial invariant of the link, such as HOMFLYPT.
“Counting minimal surfaces” needs to be interpreted carefully here, similar to how Gromov-Witten invariants “count” J-holomorphic curves. Indeed I will explain how this “minimal surface polynomial" can be seen as a Gromov-Witten invariant for the twistor space of hyperbolic 4-space. This leads naturally to a new class of infinite-volume 6-dimensional symplectic manifolds with well behaved counts of J-holomorphic curves. This gives more potential knot invariants, for knots in 3-manifolds other than the 3-sphere. It also enables the counting of minimal surfaces in more general Riemannian 4-manifolds, besides hyperbolic space.
Dans la même collection
-
Y. Lai - A family of 3d steady gradient Ricci solitons that are flying wings
LaiYiWe find a family of 3d steady gradient Ricci solitons that are flying wings. This verifies a conjecture by Hamilton. For a 3d flying wing, we show that the scalar curvature does not vanish at
-
D. Tewodrose - Limits of Riemannian manifolds satisfying a uniform Kato condition
TewodroseDavidPresentation of a joint work with G. Carron and I. Mondello where we study Kato limit spaces.
-
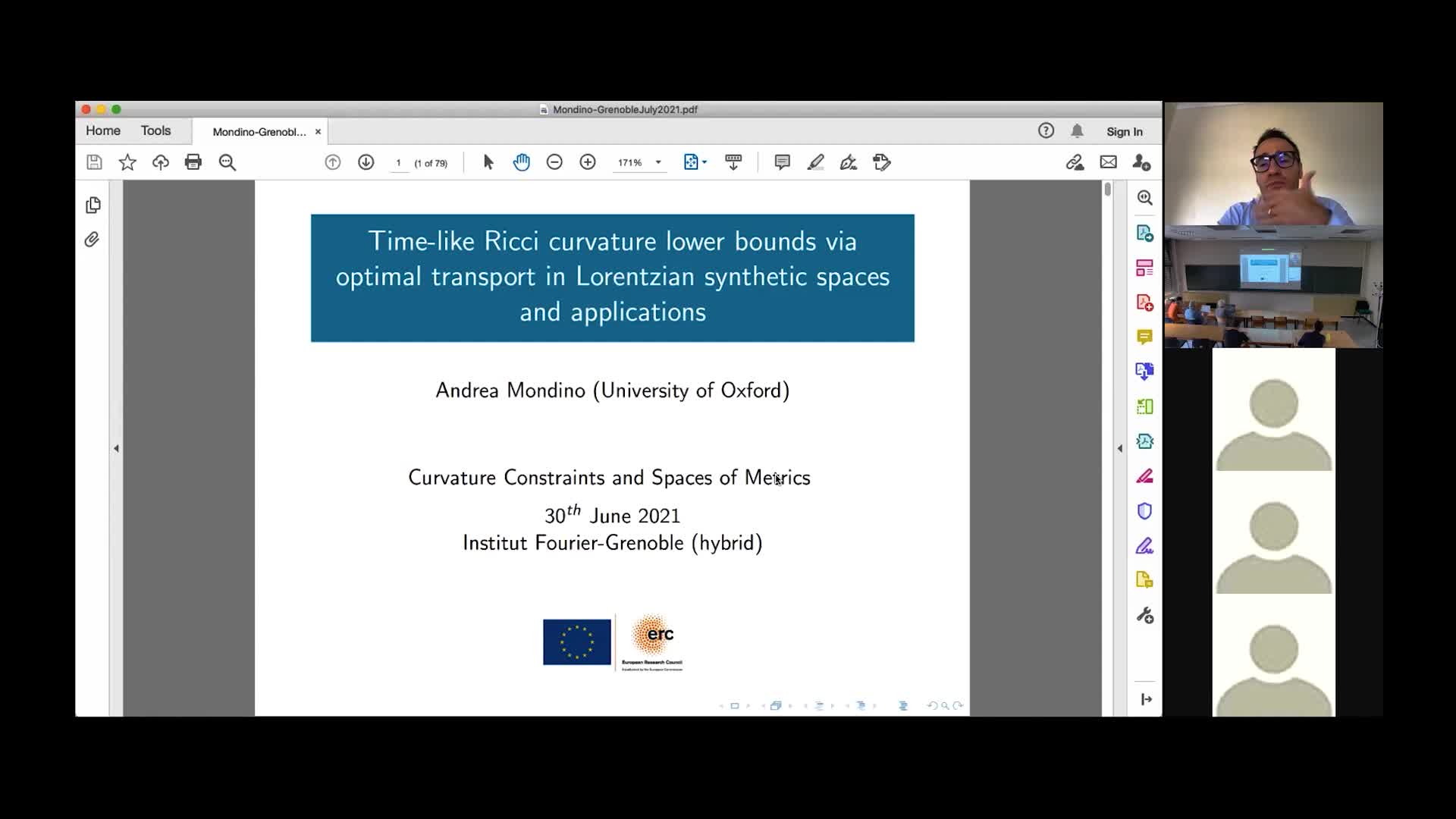
A. Mondino - Time-like Ricci curvature bounds via optimal transport
MondinoAndreaThe goal of the talk is to present a recent work in collaboration with Cavalletti (SISSA) on optimal transport in Lorentzian synthetic spaces. The aim is to set up a “Lorentzian analog” of the
-
M. Lesourd - Positive Scalar Curvature on Noncompact Manifolds and the Positive Mass Theorem
LesourdMartinThe study of positive scalar curvature on noncompact manifolds has seen significant progress in the last few years. A major role has been played by Gromov's results and conjectures, and in
-
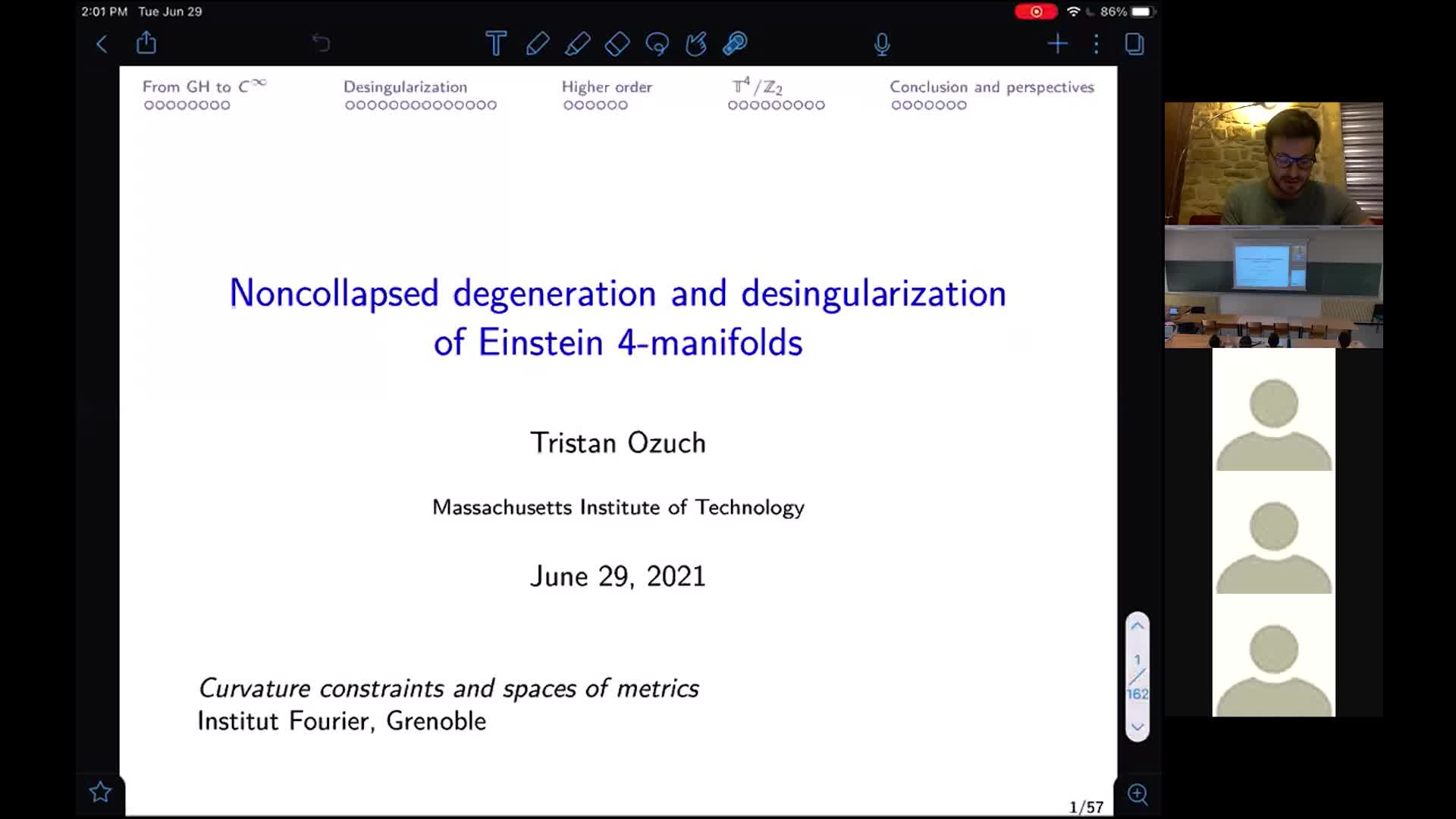
T. Ozuch - Noncollapsed degeneration and desingularization of Einstein 4-manifolds
OzuchTristanWe study the noncollapsed singularity formation of Einstein 4-manifolds. We prove that any smooth Einstein 4-manifold close to a singular one in a mere Gromov-Hausdorff (GH) sense is the result
-
C. Li - Classifying sufficiently connected PSC manifolds in 4 and 5 dimensions
LiChaoIn this talk, I will discuss some recent developments on the topology of closed manifolds admitting Riemannian metrics of positive scalar curvature. In particular, we will prove if a closed PSC
-
P. Burkhardt - Pointwise lower scalar curvature bounds for C0 metrics via regularizing Ricci flow
Burkhardt-GuimPaulaWe propose a class of local definitions of weak lower scalar curvature bounds that is well defined for C0 metrics. We show the following: that our definitions are stable under greater-than-second
-
R. Bamler - Compactness and partial regularity theory of Ricci flows in higher dimensions
BamlerRichard H.We present a new compactness theory of Ricci flows. This theory states that any sequence of Ricci flows that is pointed in an appropriate sense, subsequentially converges to a synthetic flow.
-
J. Wang - Topological rigidity and positive scalar curvature
WangJianIn this talk, we shall describe some topological rigidity and its relationship with positive scalar curvature. Precisely, we will present a proof that a complete contractible 3-manifold with
-
D. Semola - Boundary regularity and stability under lower Ricci bounds
SemolaDanieleThe theory of non smooth spaces with lower Ricci Curvature bounds has undergone huge developments in the last thirty years. On the one hand the impetus came from Gromov’s precompactness theorem
-
D. Stern - Harmonic map methods in spectral geometry
SternDanielOver the last fifty years, the problem of finding sharp upper bounds for area-normalized Laplacian eigenvalues on closed surfaces has attracted the attention of many geometers, due in part to
-
R. Perales - Recent Intrinsic Flat Convergence Theorems
PeralesRaquelThéorèmes récents de convergence plane intrinsèque
Sur le même thème
-
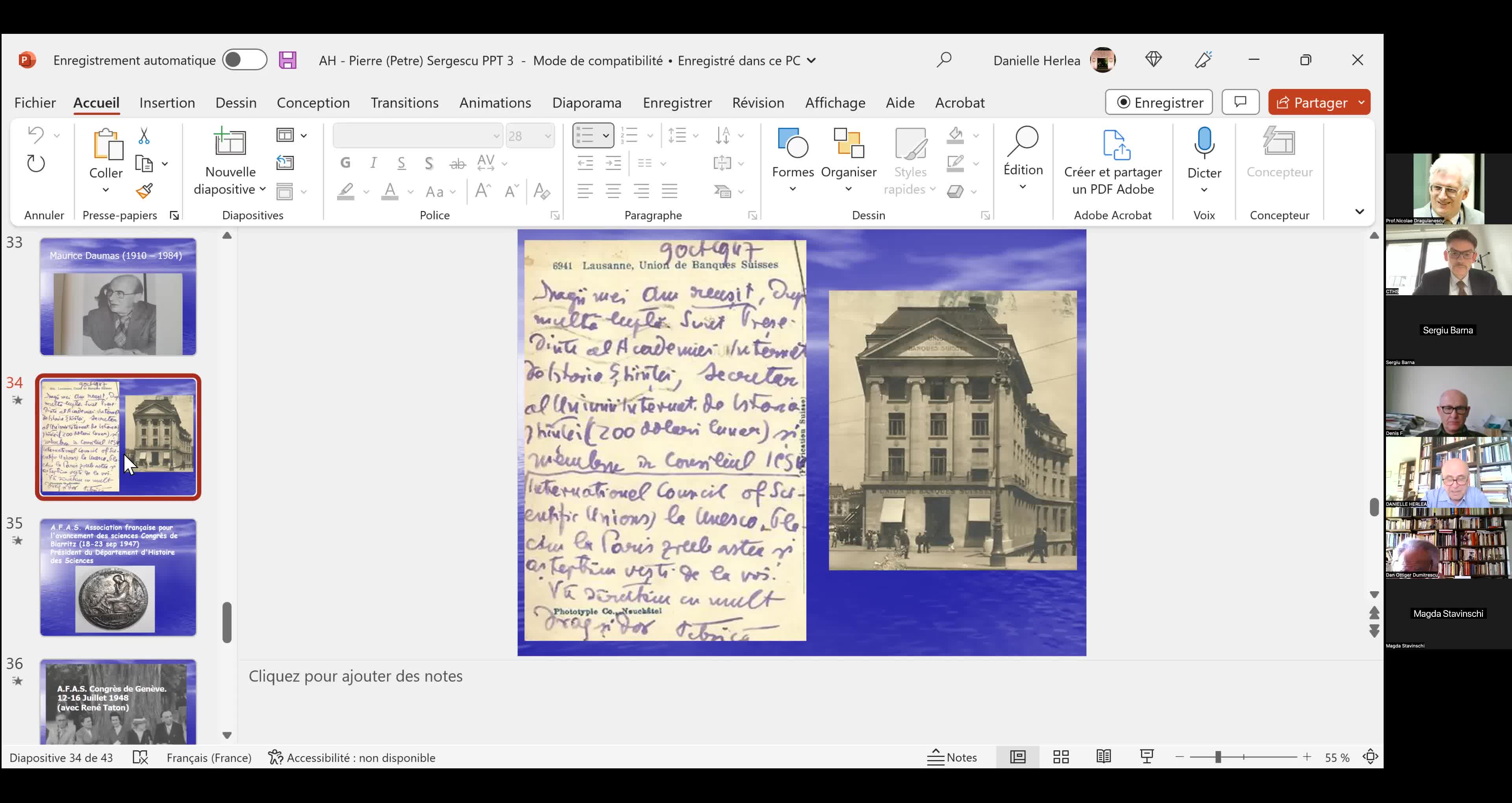
"Le mathématicien Petre (Pierre) Sergescu, historien des sciences, personnalité du XXe siècle"
HerléaAlexandreAlexandre HERLEA est membre de la section « Sciences, histoire des sciences et des techniques et archéologie industrielle » du CTHS. Professeur émérite des universités, membre effectif de l'Académie
-
Webinaire sur la rédaction des PGD
LouvetViolaineRédaction des Plans de Gestion de Données (PGD) sous l’angle des besoins de la communauté mathématique.
-
Alexandre Booms : « Usage de matériel pédagogique adapté en géométrie : une transposition à interro…
« Usage de matériel pédagogique adapté en géométrie : une transposition à interroger ». Alexandre Booms, doctorant (Université de Reims Champagne-Ardenne - Cérep UR 4692)
-
R. Bamler - Compactness and partial regularity theory of Ricci flows in higher dimensions
BamlerRichard H.We present a new compactness theory of Ricci flows. This theory states that any sequence of Ricci flows that is pointed in an appropriate sense, subsequentially converges to a synthetic flow.
-
C. Li - Classifying sufficiently connected PSC manifolds in 4 and 5 dimensions
LiChaoIn this talk, I will discuss some recent developments on the topology of closed manifolds admitting Riemannian metrics of positive scalar curvature. In particular, we will prove if a closed PSC
-
J. Wang - Topological rigidity and positive scalar curvature
WangJianIn this talk, we shall describe some topological rigidity and its relationship with positive scalar curvature. Precisely, we will present a proof that a complete contractible 3-manifold with
-
T. Ozuch - Noncollapsed degeneration and desingularization of Einstein 4-manifolds
OzuchTristanWe study the noncollapsed singularity formation of Einstein 4-manifolds. We prove that any smooth Einstein 4-manifold close to a singular one in a mere Gromov-Hausdorff (GH) sense is the result
-
D. Tewodrose - Limits of Riemannian manifolds satisfying a uniform Kato condition
TewodroseDavidPresentation of a joint work with G. Carron and I. Mondello where we study Kato limit spaces.
-
A. Mondino - Time-like Ricci curvature bounds via optimal transport
MondinoAndreaThe goal of the talk is to present a recent work in collaboration with Cavalletti (SISSA) on optimal transport in Lorentzian synthetic spaces. The aim is to set up a “Lorentzian analog” of the
-
M. Lesourd - Positive Scalar Curvature on Noncompact Manifolds and the Positive Mass Theorem
LesourdMartinThe study of positive scalar curvature on noncompact manifolds has seen significant progress in the last few years. A major role has been played by Gromov's results and conjectures, and in
-
P. Burkhardt - Pointwise lower scalar curvature bounds for C0 metrics via regularizing Ricci flow
Burkhardt-GuimPaulaWe propose a class of local definitions of weak lower scalar curvature bounds that is well defined for C0 metrics. We show the following: that our definitions are stable under greater-than-second
-
R. Perales - Recent Intrinsic Flat Convergence Theorems
PeralesRaquelThéorèmes récents de convergence plane intrinsèque
