Chapitres
- Présentation d'Edouard Brézin01'42"
- Introduction d'Edouard Brézin01'48"
- Rappels historiques11'00"
- La mécanique quantique05'54"
- Les systèmes dynamiques14'27"
- L'électromagnétisme15'53"
- La gravitation03'06"
- Conclusion de Edouard Brézin02'09"
- Questions, partie 110'13"
- Questions, partie 209'38"
Notice
Physique et mathématiques
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
La physique et les mathématiques sont étroitement mêlées depuis toujours. Tantôt c'est la première qui conduit à développer les mathématiques impliquées par les lois de la nature, tantôt des structures mathématiques élaborées sans référence au monde extérieur se trouvent être précisément adaptées à la description de phénomènes découverts pourtant postérieurement. C'est là l'efficacité déraisonnable des mathématiques dans les sciences de la nature dont parlait Eugène Wigner. Jamais les interactions entre physique et mathématiques n'ont été plus intenses qu'à notre époque, jamais la description des phénomènes naturels n'a requis des mathématiques aussi savantes qu'aujourd'hui. Pourtant il est important de comprendre la différence de nature entre ces deux disciplines. La physique n'établit pas de théorèmes ; jusqu'à présent elle se contente de modèles dont les capacités à prédire, et la comparaison avec l'expérience établissent la validité, avec une économie dans la description et une précision parfois confondantes. Néanmoins nous savons que tous les modèles dont nous disposons actuellement, toutes les lois, ne sont que des descriptions "effectives" comme l'on dit aujourd'hui, c'est-à-dire adaptées aux échelles de temps, de distance, d'énergie avec lesquelles nous observons, mais dont nous savons de manière interne, avant même que des phénomènes nouveaux les aient invalidées, qu'elles sont inaptes à aller beaucoup plus loin. Y aura t-il une description définitive qui, tel un théorème, s'appliquerait sans limitations? Ce rêve d'une théorie ultime, où la physique rejoindrait les mathématiques, caressé par certains, laisse beaucoup d'autres sceptiques ; quoiqu'il en soit la question ne sera certainement pas tranchée rapidement.
Thème
Documentation
Documents pédagogiques
Transcription* de la 573e conférence de lUniversité de tous les savoirs prononcée le 16 juin 2005
Par Edouard Brezin: « Physique et Mathématiques »
Je remercie tout d'abord l'UTLS d'avoir donné la parole aux physiciens car 2005 est l'année mondiale de la physique. Cette célébration est justifiée par le centième anniversaire de la publication d'articles d'Albert Einstein qui, dans trois domaines différents, ont changé complètement notre vision du monde. C'est aussi l'occasion pour les scientifiques français de présenter la science vivante, et de nous demander ce que ferait peut-être Einstein s'il était parmi nous aujourd'hui.
Physique et mathématiques : des histoires étroitement mêlées
Sans vouloir entièrement la retracer commençons par évoquer quelques étapes de cette route où physique et mathématiques se sont croisées, suivies, ignorées, rejointes, avant d'en arriver à la période contemporaine où se posent des questions qu'il n'y a pas très longtemps, personne ne pouvait formuler.
Longtemps mathématiques et sciences de la Nature ont été si étroitement mêlées que la différence nétait sans doute pas réellement explicitée. Que l'on se souvienne que géométrie veut dire littéralement « mesure de la Terre », et que les mathématiques furent formulées pendant très longtemps pour décrire des objets suggérés par le monde qui nous entoure.
En voici quelques exemples.
Pythagore et la diagonale du carré
Commençons avec Pythagore, astronome mathématicien, qui fut le premier à démontrer le théorème qui porte son nom, le théorème de Pythagore (que les Babyloniens connaissaient). Pythagore considère un carré de côté 1 : il a démontré que la longueur de sa diagonale valait (racine carrée de 2). Mais à cette époque, seuls les rapports de deux nombres entiers, les fractions, sont considérés comme des nombres. Pythagore cherche alors à exprimer (racine carrée de 2) comme un de ces nombres et, comme il est fin mathématicien, il démontre que (racine carrée de 2) ne peut pas s'écrire comme un rapport de deux nombres entiers. Le carré existe, sa diagonale existe, mais ce nombre semble ne pas exister ! C'est un sentiment inconcevable de contradiction entre la Nature et les mathématiques qui apparaît, alors que pour Pythagore elles sont parties d'un même tout.
Archimède et les volumes
Archimède était un génie absolument extraordinaire. Il a fait graver sur sa tombe une sphère et un cylindre. Fin mathématicien, il avait réussi à calculer des volumes, comme celui de la sphère, par exemple, ou encore celui donné par l'intersection de deux cylindres ( Cf. figure 1). La méthode qu'il avait introduite est une méthode intellectuellement très semblable à celle qui mettra vingt siècles à aboutir avec Newton et Leibniz, le calcul intégral. En effet pour calculer ces volumes, Archimède coupait en tranches comme on apprend à la faire lorsque l'on fait du calcul différentiel.
figure 1
Néanmoins, comme vous le savez, son génie de physicien n'était pas moins grand. Lhistoire est fort célèbre : le roi de Syracuse avait commandé une couronne en or massif mais il soupçonnait le bijoutier de l'avoir trompé. Il demanda alors à Archimède de déterminer si la couronne était bien en or massif. Après une réflexion très profonde Archimède comprit la nature de la force exercée par un liquide sur un corps immergé et répondit ainsi à la question du roi.
Galilée, père fondateur de la physique
Avançons de presque deux mille ans. Pourquoi aller si vite et passer ainsi deux mille ans de sciences ? Chacun est libre de son opinion. Je crois tout de même que le dogmatisme des églises y est pour quelque chose. Les ennuis de Galilée avec les églises sont célèbres même si l'issue en est moins dramatique que pour Giordano Bruno.
Nous sommes au XVIème siècle et Galilée écrit cette phrase célébrissime :
« La philosophie est écrite dans ce grand livre qui se tient constamment ouvert devant les yeux, je veux dire l'Univers. Mais elle ne peut se saisir si tout d'abord on ne se saisit point de la langue et si on ignore les caractères dans laquelle elle est écrite. Cette philosophie, elle est écrite en langue mathématique. Ses caractères sont des triangles, des cercles et autres figures géométriques, sans le moyen desquelles il est impossible de saisir humainement quelque parole, et sans lesquelles on ne fait qu'erre vainement dans un labyrinthe obscur. »
C'est un texte remarquable, toujours aussi pertinent de nos jours.
Newton et le calcul différentiel
La méthode de Newton est une des méthodes d'interaction de la physique et des mathématiques. Newton comprend la loi de la dynamique - la célèbre loi de Newton - qui dit que la force est égale à la masse qui multiplie l'accélération. Et à partir de ce moment-là on rentre déjà dans un paysage assez abstrait, assez difficile mathématiquement car l'accélération c'est la variation de la vitesse, la vitesse étant elle-même la variation de la position. La force, elle, est donnée en fonction de la position. On se trouve en présence d'un problème mathématique où la deuxième variation - que les mathématiciens appellent la « dérivée seconde » - de la position est donnée en fonction de la position. Pour arriver à résoudre cela, Newton invente le calcul différentiel et intégral. Et ayant compris que la force d'attraction gravitationnelle est inversement proportionnelle au carré de la distance, Newton retrouve les lois sur le mouvement des planètes que Kepler avait établies par l'observation.
La déduction des lois de Kepler est bien un théorème de mathématiques, et ces mathématiques ne sont ni très simples, ni intuitives. En d'autres termes, il faut distinguer, dans les problèmes, ce qui est mathématique et ce qui est physique. Ce qui est physique, c'est pourquoi la force est la masse multipliée par l'accélération (Descartes croyait que c'était la masse fois la vitesse), c'est comprendre pourquoi la force d'attraction est inversement proportionnelle au carré de la distance entre deux corps massifs, et pas au cube ou à la puissance 2,1. En revanche, admettant ces deux hypothèses, démontrer les lois de Kepler ce sont réellement des mathématiques. Et c'est ce que Newton a fait. C'était un très grand scientifique.
Fourier et la chaleur
Un autre exemple très extraordinaire des croisements entre physique et mathématiques vient avec Joseph Fourier au XIXème siècle. Dans un article sur la théorie analytique de la chaleur dans les Comptes Rendus de l'Académie des Sciences en 1822, Fourier s'interroge : lorsque l'on a deux corps en contact, l'un étant plus chaud que l'autre, comment écrire le flux de chaleur du corps chaud vers le corps froid ? Il construit sa théorie et il aboutit à une équation aux dérivées partielles qu'il faut résoudre. Et dans cet article où il introduit la notion de flux de chaleur, Fourier introduit aussi ce qu'on appelle dans le monde entier la transformation de Fourier. C'est l'un des instruments les plus puissants des mathématiques et de la physique.
Avec Newton et Fourier ce sont donc des problèmes de physique bien posés qui ont conduit à développer des outils mathématiques nouveaux, voire révolutionnaires. Mais, comme on va le voir, cela ne se passe pas toujours ainsi.
Gauss l'universel
Il faut aussi mentionner Gauss, mathématicien éminent, surnommé souvent le « Prince des mathématiques ». La physique lui doit un traité de mécanique céleste, le développement d'un magnétomètre et une des lois de l'électromagnétisme porte son nom. Ainsi, à cette époque, un esprit universel comme Gauss s'intéresse aussi bien aux deux disciplines.
La physique au XXème siècle
Mais si l'on se rapproche de la période contemporaine, il est frappant que la physique du XXème siècle a souvent fait appel à des mathématiques qui avaient été développées antérieurement, pour leur seule beauté et richesse intrinsèques. Cette beauté des mathématiques, leur logique interne, conduit les mathématiciens dans leurs recherches. Deux exemples où les mathématiques nécessaires à la physique lont précédée sont fournis par la relativité générale et la mécanique quantique.
La relativité générale d'Einstein
Le travail de Bernhard Riemann, grand mathématicien mort hélas jeune, précède celui d'Einstein sur la relativité générale, Il a eu l'idée de définir la géométrie de l'espace par une métrique, c'est-à-dire par lexpression de la distance entre deux points voisins. Ceci permet de définir toutes sortes de géométries. Des géométries simples, comme la géométrie euclidienne, mais également bien d'autres. C'est un outil considérable et cest exactement celui dont a besoin Einstein. Il comprend que la présence de matière change la géométrie de l'espace-temps et qu'en retour cette géométrie détermine les trajectoires des objets massifs et de la lumière. Ce sont les masses qui déforment la géométrie, et la géométrie déformée définit les trajectoires de tous les objets célestes. Cette théorie s'appelle la relativité générale. Einstein va passer beaucoup de temps, avec son ami Besso, pour comprendre les travaux de Riemann afin de s'en servir dans sa théorie.
La mécanique quantique
Heisenberg et les matrices
La mécanique quantique a deux sources indépendantes. L'une a été développée par Werner Heisenberg qui comprit que la mesure d'une quantité physique modifiait inéluctablement l'état d'un système. Si on mesure une des ses propriétés, inéluctablement on modifie létat du système. Heisenberg montre que si on mesure d'abord la position puis la vitesse d'un corps en mouvement, ou bien si lon mesure d'abord sa vitesse puis sa position, on ne trouve pas les mêmes résultats. Les résultats des mesures dépendent donc de l'ordre dans lequel on les fait. C'est une structure mathématique compliquée et Heisenberg ne sait pas très bien comment aborder cette question. Mais il était bon mathématicien et il connaissait des travaux du XIXème siècle qui avaient défini ce qu'on appelle des matrices, c'est-à-dire des objets qui décrivent des opérations sur un espace. Si on veut décrire par exemple les rotations d'un dé, selon qu'on le fait tourner d'abord autour de l'axe vertical puis autour d'un axe horizontal ou bien que l'on choisisse l'ordre inverse, le dé n'est pas dans la même position. Tous ceux qui ont un jour joué avec un Rubik's cube savent bien que les rotations ne commutent pas entre elles mais dépendent de l'ordre dans lequel on les fait. Heisenberg utilise là des mathématiques préexistantes, qui avaient été développées abstraitement, mais dont il se rend compte qu'elles sont indispensables à sa description de la mesure.
De Broglie, Schrödinger et les fonctions d'onde
L'autre source de la mécanique quantique est due à de Broglie et à Schrödinger. Ce dernier comprend profondément ce que disait de Broglie, de la dualité onde-particule. Erwin Schrödinger, Autrichien, qui avait fuit le nazisme pour aller à Dublin, (contrairement à Heisenberg qui a travaillé sur la bombe allemande, heureusement sans succès) comprend que si une particule est en même temps une onde, sa propagation doit être décrite par une équation d'onde qui décrit les variations spatiales et temporelles de cette onde. Il comprend quelle est cette équation, mais le formalisme devient extrêmement abstrait : l'état d'un système physique est un vecteur d'un espace abstrait, qu'avait introduit au début du XXème siècle le grand mathématicien David Hilbert, espace infini, avec une structure complexe[1]. On voit que, chacune des deux sources de la mécanique quantique (qui se révèleront in fine équivalentes) on fait appel à des mathématiques abstraites, inventées en suivant la logique propre des mathématiques et qui néanmoins sont indispensables pour décrire la physique.
La déraisonnable efficacité des mathématiques
Ceci conduit un physicien, Eugène Wigner, prix Nobel pour ses travaux de physique nucléaire, qui a beaucoup contribué à la physique théorique du XXème siècle, à écrire un article en 1960 intitulé « de la déraisonnable efficacité des mathématiques dans les sciences de la Nature ». C'est en gros une rationalisation de ce que je viens de dire. Wigner s'émerveille de voir que des structures qui paraissaient complètement éthérées, sans rapport initial avec le monde actuel, bien quelles ne soient pas issues d'une réflexion sur le monde ou la Nature, se trouvent néanmoins avoir leur place, et ô combien, dans la description du monde.
La complexité croissante des mathématiques
Le dernier portrait que je vais évoquer est celui d'un des grands héros de la physique théorique du XXème siècle Richard Feynman. Lors d'une conférence publique il déclara :
« Chacune de nos lois s'énonce sous forme mathématique et en des termes souvent complexes et abstraits. La loi de gravitation telle que Newton l'énonça n'utilise que des mathématiques assez simples mais au fur et à mesure que nous avançons, les énoncés deviennent de plus en plus complexes. Pourquoi ? Je n'en ai pas la moindre idée. Le drame de cette conférence c'est justement que je dois vous faire comprendre qu'on ne peut sérieusement expliquer la beauté des lois de la Nature et surtout de la faire ressentir à des gens qui n'ont aucune connaissance profonde des mathématiques. »
La période contemporaine
La période contemporaine est caractérisée par des interactions constantes entre physique et mathématiques, dans beaucoup de directions différentes dont voici, sans soucis d'exhaustivité, quelques exemples.
Les systèmes dynamiques et le chaos
L'étude des systèmes dynamiques doit beaucoup à Henri Poincaré, mathématicien français né à Nancy à la fin du XIXème siècle et qui a travaillé au début du XXème, grand mathématicien et grand physicien également. Un système dynamique est un système dont on veut suivre l'évolution temporelle régie par des équations d'évolution parfaitement définies et déterministes. Il n'y a aucun hasard dans un système dynamique, tout y est bien connu. Comme le mouvement des planètes dont les équations sont connues, des molécules d'un fluide, de l'atmosphère... La figure 2 montre l'évolution d'un système dynamique en deux dimensions pendant un petit intervalle de temps. Le point de coordonnées (x,y) est transformé par la formule en le point (x',y'). Pour avoir l'évolution temporelle du système, on applique la formule, toujours la même, un grand nombre de fois et on suit la trajectoire du point à chaque étape.
figure 2
C'est un système dynamique des plus simples mais les trajectoires sont déjà très complexes et on voit apparaître ce qu'on appelle des attracteurs étranges. La mécanique des fluides est un exemple de domaine où la complexité des comportements possibles est très grande.
Poincaré fut sans doute le premier à poser la question de la stabilité du système solaire. Le système solaire, même réduit à la Terre, à la Lune et au Soleil, est un système compliqué. Pendant longtemps on a cru que les comportements complexes, comme la turbulence d'un fluide, étaient dus à la complexité du système, à cause du très grand nombre de molécules constituantes. Mais l'étude de petits modèles apparemment simples comme celui qu'avait introduits Édouard Lorenz, un météorologue, ou Hénon un astrophysicien niçois, montra la complexité que l'on pouvait atteindre dans de très petits systèmes. En 1971 les physiciens-mathématiciens Ruelle (qui travaille toujours à Bures-sur-Yvette) et Takens démontraient que de très petits systèmes étaient presque toujours chaotiques sauf si on choisit un système très approprié. Le terme « chaos » désigne la sensibilité extrême aux conditions initiales. Cette sensibilité fait diverger les trajectoires de deux points, initialement très proches. On l'appelle souvent l'effet papillon.
Un astrophysicien de l'Université de Paris VII, Jacques Laskar, spécialiste des mouvements planétaires, a étudié les mouvements du système solaire en utilisant des méthodes nouvelles faisant appel à la puissance des moyens de calcul contemporains. Voici ses commentaires :
« Cette méthode a permis de démontrer que le mouvement des planètes et en particulier les planètes inférieures, Mercure, Vénus, la Terre et Mars avaient un temps caractéristique de l'ordre de cinq millions d'années. Cela signifie que si l'on a deux solutions initialement proches, leurs trajectoires vont s'éloigner non pas linéairement mais de façon exponentielle. Ainsi, si l'on a une incertitude de quinze mètres sur la position actuelle de la Terre, au bout de dix millions d'années nous aurons une erreur de cent cinquante mètres, en soit cette valeur est dérisoire, l'éphéméride ne pourrait prétendre avoir une telle précision. Mais si on prolonge les calculs sur cent millions d'années on aura une incertitude de cent cinquante millions de kilomètres, c'est la dimension du système solaire. Ce qui signifie que nous ne pourrons absolument plus situer au bout de cent millions d'années, la position de la Terre dans le système solaire. Nous sommes dans l'impossibilité de calculer cette position aujourd'hui, mais nous le serons également dans mille ans ou dans un million d'années. Ce n'est pas une question de limitation de nos connaissances ou de nos calculs. Quinze mètres représentent en fait la perturbation engendrée par le passage d'un astéroïde. Si nous désirons garder une telle précision à long terme il faudrait inclure dans notre modèle tous les objets engendrant des perturbations de l'ordre de quinze mètres, autant dire des centaines de milliers de corps qui peuplent le système solaire, astéroïdes, comètes, satellites gardiens et fragments de toutes sortes. Si l'on veut aller encore plus loin passer d'une précision de quinze mètres à quinze microns, au lieu d'avoir une erreur de cinquante millions de kilomètres au bout de cent millions d'années, on aura cent cinquante millions de kilomètres au bout de cent soixante millions d'années. Cela n'aura pas changé grand-chose. Et nous avons donc vraiment une limite pratique aux capacités à prévoir l'avenir des mouvements du système solaire. »
Voilà une chose que l'on ne savait pas au temps de Poincaré et que la mécanique céleste a récemment permis de comprendre.
La physique statistique
Un autre grand domaine de fertilisation, croisé entre mathématiques et physique est la physique statistique. Depuis la fin du XIXème siècle et les travaux de Maxwell, de Boltzmann, inventeurs de cette science, on sait qu'il est illusoire, voire inutile, pour décrire la matière, d'en suivre tous les degrés de liberté. Si on considère un morceau de métal, par exemple, on sintéresse à savoir s'il est conducteur ou isolant, si sa température augmente vite ou lentement lorsqu'on le chauffe, pourquoi il est noir ou rouge... On n'a pas besoin de savoir, contrairement au problème des trajectoires des planètes, quelle est la position des milliards de milliards de molécules qui le constituent. Dailleurs à supposer que l'on puisse le faire - ce qui n'est pas le cas - il serait bien difficile dy lire la réponse aux questions que nous posions.
Une méthode probabiliste
La méthode « ordinaire », celle que lon met en Suvre pour les systèmes planétaires, est donc inopérante pour la description de la matière. La méthode qui a permis, grâce à Maxwell et Boltzmann et bien d'autres à leur suite, de comprendre la matière, est une méthode a priori paradoxale : c'est une méthode statistique qui utilise des concepts probabilistes, cest-à-dire modélisent le hasard. Si lon joue à la roulette une seule fois, le fait de savoir qu'il y a trente-six résultats possibles ne fournit aucune aide pour gagner. Mais le propriétaire du casino, qui enregistre des milliers de paris, peut utiliser des outils statistiques, telle la loi des grands nombres, pour prédire avec une certitude quasi-complète non pas un résultat ponctuel, mais ce que sera l'ensemble des résultats. C'est là le miracle de la physique statistique qui utilise le gigantisme du nombre datomes, pour utiliser le hasard et néanmoins prédire de manière en pratique certaine.
L'énergie et le désordre
La mécanique statistique, c'est donc l'utilisation des probabilités pour relier la matière macroscopique à ses atomes. Il y a des cas singuliers où la matière change complètement d'état, par exemple l'eau qui devient vapeur lorsqu'on la chauffe, ou qui gèle si on la refroidit. Dans ce dernier exemple, le refroidissement ne change rien aux molécules d'eau individuelles, il ne change pas non plus l'interaction entre les molécules d'eau qui est complètement indépendante de la température. La notion de température bien que familière, est en réalité assez subtile : la température pour les physiciens, c'est le paramètre qui arbitre entre deux tendances opposées de la matière : au zéro absolu tout système se range dans létat bien ordonné dont l'énergie est la plus basse possible, mais lorsque la température augmente le désordre (ou entropie) contrarie cette tendance à la régularité et finit par lemporter. Quand de l'eau juste au-dessus de zéro degré Celsius passe juste en dessous de cette température, des milliards de molécules d'eau, complètement désordonnées dans le liquide, s'ordonnent spontanément. Elles forment un réseau cristallin, invisible mais bien réel. Ces comportements singuliers, les transitions de phase, ont longtemps posé problème et il y a eu au cours des dernières années de nombreux échanges entre mathématiques et physique à ce sujet.
Illustration : le modèle d'Ising
Pour illustrer ces phénomènes de transition, il existe un modèle décole, un prototype qui se révèle en fait très universel dans sa portée, appelé le modèle d'Ising. On le représente sous forme d'un damier de carrés pouvant être dans un état blanc ou noir. L'énergie de deux carrés voisins est grande lorsqu'ils sont de couleurs différentes et faible lorsqu'ils sont de même couleur. Diminuer l'énergie revient ainsi à uniformiser la couleur du damier ; le désordre se traduit par un mélange aléatoire des deux couleurs. Selon la température la minimisation de lénergie qui ordonne les carrés, ou lentropie qui les distribue au hasard vont dominer. À haute température le système évolue rapidement, les carrés changent fréquemment de couleur, mais les couleurs restent mélangées : c'est le désordre qui l'emporte. En revanche à basse température, le système évolue plus lentement, de grandes régions de même couleur apparaissent et si on attend assez longtemps, une couleur va dominer très largement l'autre : c'est l'énergie qui l'emporte. La transition de phase a lieu à la température où énergie et désordre s'équilibrent ( Cf. figure 3).
figure 3
Chaque carré peut être rouge ou bleu. Deux carrés voisins de même couleur « sattirent ».
Ce modèle paraît très simple, mais le résoudre a été un tour de force technique d'un grand physicien-mathématicien qui s'appelait Lars Onsager. Cela a été aussi l'ouverture vers une interaction entre physique et mathématiques qui s'appelle la théorie des systèmes intégrables et qui est très active aujourd'hui.
Autres domaines contemporains
Un dernier exemple de systèmes qui appartient à la même nature de question sont les systèmes auto-similaires, qu'on appelle aussi systèmes fractals. Ce système ( Cf. figure 4) est simple, il est auto-similaire c'est-à-dire que l'on retrouve les mêmes structures à toutes les échelles vers l'infiniment petit. Les propriétés de celui qui est ici montré (la diffusion limitée par lagrégation) ne sont pas encore comprises aujourd'hui malgré beaucoup d'années d'efforts de mathématiciens aussi bien que de physiciens. Ceci constitue un exemple de problème, lié à des phénomènes de croissance cristalline et de systèmes en évolution, que l'on se pose aujourd'hui.
figure 4
Les interactions fondamentales
Venons-en maintenant aux quatre interactions fondamentales l'électromagnétisme, les forces nucléaires faibles ou fortes et les forces gravitationnelles. Tous les phénomènes de la Nature sont régis par ces interactions, on n'a encore jamais vu de contre-exemple.
L'électromagnétisme
L'électromagnétisme illustre bien l'état de nos connaissances et les questions qui se posent à l'interaction entre physique et mathématiques. Il faudra pour cela quelques formules dont le sens n'est pas important, mais qui permettent de cerner la problématique. Concentrons-nous sur un problème particulier celui du facteur gyromagnétique de l'électron. L'électron est une petite particule constitutive des atomes, chargée négativement. Un atome est constitué d'électrons et d'un tout petit noyau au centre. On sait grâce à la mécanique quantique, depuis les années 1920, que l'électron possède une caractéristique nommée spin (une sorte de flèche interne). Ce spin donne à un électron, comme à un aimant, un moment magnétique (c'est-à-dire un pôle nord et un pôle sud), et ce moment magnétique µ est proportionnel au spin S :
µ = g (e/2m) S
Ici apparaissent la charge e et la masse m de l'électron. Si l'électron était un objet classique (en omettant relativité et mécanique quantique), le nombre g vaudrait exactement 1. Les expériences donnent g=2,0023193043737. (C'est une des mesures expérimentales les plus précises ayant jamais été faites avec douze chiffres significatifs.) Que dit la théorie pour ce facteur g ? La théorie quantique non relativiste donne g=1, erreur de 100 %. Dirac, physicien anglais des années 1920-1930, a développé une théorie relativiste de l'électron en 1928 et il a trouvé g=2, ce qui est presque exact. Mais les physiciens se demandaient si on peut faire mieux et comprendre la petite différence entre g et 2. La réponse est oui. La technique employée s'appelle la théorie quantique des champs, plus précisément lélectrodynamique quantique. Dans la théorie de Dirac, l'électron obéit à la mécanique quantique, mais le champ électromagnétique dans lequel est plongé l'électron, lui, est classique. Or il possède lui aussi des fluctuations quantiques. La théorie qui a été développée procède par approximations successives en se servant d'un nombre qu'on appelle la constante de structure fine et qui est vaut
alpha=e²/(2 pi h c)
(e est la charge de l'électron, c la vitesse de la lumière h la constante de Planck) soit environ 0,007. Partons de la valeur de Dirac g=2. La première approximation rajoute 0,007 divisé par pi. Un grand physicien, Schwinger, a été récompensé par le prix Nobel pour ce calcul. Il a partagé ce prix avec Feynman et Tomonaga pour avoir montré que ce calcul pouvait se poursuivre de manière systématique, même si les calculs sont longs et difficiles. Quand on inclut cette première correction au résultat de Dirac, on n'est plus très loin de l'expérience ; au fur et à mesure que l'on calcule les autres termes on se rapproche du résultat expérimental. L'accord entre théorie et expérience est confondant. C'est le plus grand accord jamais observé entre une théorie et une expérience.
Les chiffres 0,656 et 2,362 sont les valeurs numériques d'expressions très compliquées où intervient la fonction zeta de Riemann :
C'est pire encore pour le suivant qui a été calculé en 1996. En conclusion, cette théorie est d'une grande complexité mathématique, mais elle marche merveilleusement.
La renormalisation et ses limites
Malgré tout, de nombreuses questions se sont vite posées sur la validité du procédé d'approximations successives que jai décrit. Ce procédé part d'un résultat approché, puis on ajoute une première perturbation puis une perturbation encore plus petite. Mais finalement le résultat est satisfaisant.
Valse des paramètres
Cette méthode par approximations successives a posé des questions, difficiles et abstraites, de deux ordres. La méthode, qui a fait le succès de ce calcul, repose sur un concept qui porte le nom de « renormalisation ». Dans la théorie telle qu'ils l'avaient développée, Feynman, Schwinger et dautres ont rencontré des objets mathématiques dépourvus de toute signification : des intégrales divergentes, des objets totalement infinis ; pour régler ce problème ils ont introduit arbitrairement une toute petite longueur en-deçà de laquelle on sinterdit de pénétrer. Les quantités physiquement mesurables, comme par exemple la charge de l'électron ou sa masse, ne sont alors plus égales à celles introduites dans le modèle initial, mais sont remplacés par les paramètres que l'on mesure physiquement. On montre alors que lon peut saffranchir de lintroduction de la petite longueur initiale. C'est-à-dire qu'a priori l'électromagnétisme est capable de décrire les phénomènes astronomiques jusqu'aux plus courtes distances et on n'a pas besoin de longueur fondamentale. Ce processus magnifique, que certains continuent de regarder comme un tour de passe-passe génial, est à l'origine du prix Nobel de Feynman, Schwinger et Tomonaga.
Les approximations successives
On s'est aussi inquiété du schéma d'approximations successives, en se demandant s'il était bien défini ou en d'autres termes si lorsque l'on poursuit et que lon inclut successivement les termes suivants,, les valeurs obtenues sont toujours plus précises. Les mathématiciens diraient alors qu'un tel processus est convergent. Cette question a longtemps été discutée, mais un physicien anglais (travaillant aux Etats-Unis), Freeman Dyson, a donné des arguments qui montraient que la précision était vraisemblablement limitée et que si on continuait à calculer la série, les termes que l'on allait ajouter n'amélioreraient pas le résultat et finiraient même par le détériorer complètement. Cela n'a aucune influence pratique car quelques termes suffisent amplement, mais cela a posé une question conceptuelle. Le succès de cette méthode repose réalité sur le fait naturel que ce nombre alpha est petit. Pour des raisons, qui pour linstant nont pas reçu dexplication, on constate quil vaut 0,007297... S'il valait 0,1 ou 1 le processus employé ne marcherait pas.
La limite de l'électromagnétisme
Ce caractère a priori non contrôlé a poussé plusieurs mathématiciens à chercher une autre approche pour s'affranchir de ce processus d'approximations successives. Ils ont donc tenté de transformer cette description de l'électromagnétisme quantique en un théorème. C'est-à-dire montrer, avant même de calculer, que cette théorie était apte à décrire tous les phénomènes électromagnétiques depuis les plus grandes distances jusqu'aux plus petites, celles que l'on explore aujourd'hui avec les microscopes les plus puissants : les accélérateurs de particules (comme ceux du CERN) dont la résolution atteint quelques milliardièmes de milliardièmes de mètre (10^(-18) m).
La question posée était celle-ci : est-ce que la renormalisation est une construction ad hoc limitée ou est-elle un théorème[2] - au sens des mathématiques ? La physique a donné une réponse très paradoxale, tout à fait surprenante a priori et qui ne s'est imposée qu'après beaucoup de résistances. Jusqu'à présent les constructions que nous avons connues partaient de la physique à notre échelle pour descendre par approximations successives vers l'élémentaire. On avait ainsi la matière, puis ses molécules, les atomes, les noyaux et enfin les quarks. Mais le succès de cette électrodynamique venait de l'hypothèse que l'on pouvait descendre dans l'infiniment petit sans limite. Or quand bien même on ne sait pas distinguer expérimentalement des distances plus petites que 10^(-18) m, le milliardième de milliardième de mètre, Planck avait compris au début du XXème siècle qu'il existe une limitation à cette description : à des distances inférieures à 10^(-35) m (0,00000000000000000000000000000001 m) c'est-à-dire environ cent milliards de milliards (10^20) fois plus petite que le noyau d'un atome, il y a une longueur en dessous de laquelle la physique reste inconnue à cause de notre incapacité actuelle à réconcilier les deux percées majeures du XXème siècle : la mécanique quantique et la relativité.
Une théorie effective
Cette limitation à très courte distance a conduit à inverser le schéma de pensée et à rejeter l'idée d'aller toujours vers le plus petit. Mais alors peut-on, à partir d'une physique inconnue à très courte distance, comprendre ce qui se passe aux échelles plus grandes ? Et la réponse est venue du groupe de renormalisation, une approche qui a montré deux choses surprenantes l'une comme l'autre.
Quelle que soit la physique à courte distance - qui est inconnue, c'est la théorie de l'électromagnétisme telle que nous la connaissons qui s'applique. Elle est donc valable non pas parce qu'elle n'a pas de limitation vers l'infiniment petit comme on le croyait auparavant, mais précisément parce qu'elle est engendrée aux échelles de nos expériences qui sont grandes au regard des échelles inconnues. On dit alors que la théorie est effective.
On sait aujourd'hui qu'aux distances les plus courtes elle ne serait pas cohérente aussi petite que soit la valeur de alpha. L'électromagnétisme est donc une théorie effective, satisfaisante, mais qui porte sa propre mort. La situation est une peu différente des situations qui se sont présentées auparavant en physique. La théorie de Newton n'est pas fausse, mais elle est limitée : lorsque les vitesses se rapprochent de celle de la lumière ou lorsque les phénomènes en jeu sont des phénomènes de petites distances où il y a des effets quantiques et la théorie de Newton ne s'applique pas. Ce n'est pas pour cela qu'elle est fausse ; elle n'a pas de contradiction interne. La théorie de la relativité, qui signerait la limite fatale pour la théorie de Newton, n'est pas contenue dans cette dernière. La théorie de l'électromagnétisme ne s'applique pas au delà d'une limite connue et ce qu'il y a au-delà est inconnu.
Les forces nucléaires
Face à tout cela, au cours de la période contemporaine on a cherché à reproduire le succès de l'électromagnétisme, et cela a fonctionné pour en physique nucléaire pour les interactions nucléaires faibles et fortes. Avec l'électromagnétisme elles constituent ce qui est appelé le modèle standard, qui donne de très bons résultats mais qui comme l'électromagnétisme est une théorie effective. Il faut donc en venir à la dernière force, la gravitation.
Le cas particulier de la gravitation
À l'échelle classique, non quantique, la gravitation s'applique aux phénomènes astronomiques. Sa version moderne, la théorie de la relativité générale d'Einstein a été très importante. Elle a donné le jour à la cosmologie et à un Univers avec une histoire, car avant Einstein on pensait que l'Univers était immuable, on sait maintenant qu'il évolue.
La gravitation est une force extrêmement ténue. Nous la ressentons lorsquelle met en jeu des masses astronomiques. Cest ainsi quun électron et un proton s'attirent parce qu'ils ont des charges opposées et aussi parce qu'ils ont des masses. Le rapport de la force d'attraction due aux masses, l'attraction gravitationnelle, à la force d'attraction due aux charges est 10^(-40). La gravitation est 10^(40) fois plus petite. Elle est donc extraordinairement faible. Néanmoins nous savons que la gravitation met en jeu, aux très courtes distances, des phénomènes quantiques et leur prise en compte ne semble pas pouvoir résulter dune théorie quantique des champs, comme cest le cas pour les trois autres interactions.
La théorie des cordes
Un autre modèle s'est fait jour, appelé la théorie des cordes. Dans cette théorie l'espace est décrit non plus par des points mais par de petites cordes qui vibrent et dont toutes nos particules ne seraient que des états d'excitation. Elle est apte a priori à décrire toutes les interactions connues, mais il faut avouer quelle n'a pour l'instant permis de prédire aucun phénomène observable. Beaucoup de physiciens dans le monde y travaillent parce que cela leur semble être la seule porte ouverte face à léchec de la théorie des champs.
Imaginons que cette théorie fonctionne, quelles en seraient les conséquences ? Les calculs seraient peut-être difficiles comme ceux déjà évoqués, mais néanmoins toutes les forces de la Nature seraient connues. Est-ce qu'un jour notre description de la nature sera comme un théorème ? Est-ce que la physique sera devenue un théorème ?
Ces questions n'ont rien de scientifique aujourd'hui. Certains pensent queffectivement, cette théorie, baptisée « théorie du tout » achèvera notre description du monde comme le ferait un théorème. Il ne resterait alors que des difficultés dus à la complexité des calculs. D'autres pensent que lorsque cela sera compris il y aura encore de nouvelles questions que nous sommes tout à fait incapables de formuler aujourdhui, et que ce questionnement ne s'arrêtera jamais.
Une des questions fondamentales posée aux théoriciens des cordes porte sur le nombre alpha=0,007... Ce nombre est important parce qu'il détermine la taille des atomes, la façon d'être de notre monde. C'est un nombre absolument essentiel pour notre monde. A-t-il cette valeur pour des raisons accidentelles ? Pourrait-il en avoir d'autres ? N'existe-t-il qu'une seule solution aux équations que contemplent aujourd'hui les théoriciens ou alors des Univers de toutes natures sont-ils possibles ? Nous serions dans notre Univers tel quil est pour des raisons « accidentelles ». Sont-elles réellement accidentelles ou manquerait-il un principe ? Voilà des questions qui sont d'allure philosophique mais qui sont posées réellement aux théoriciens d'aujourd'hui et vous voyez là comment les interrogations des mathématiques et de la physique se rejoignent. Jamais l'interaction entre mathématiques et physique n'a été aussi riche et aussi stimulante qu'en ces questions que je viens d'évoquer.
[1] Complexe signifie ici que la structure fait intervenir les nombres complexes des mathématiciens pour lequel il faut introduire un nombre qui serait la racine carrée de -1 et qui généralise la notion de nombre
[2] Un théorème est une assertion toujours vraie lorsque les hypothèses le sont
Liens
La Web TV de l'enseignement superieur
Université René Descartes Paris-5Partenaire de l'université de tous les savoirs 2001-2002 Accueil dans ses locaux les conférences
la vidéo de la conférence en realL'audio de la conférence du 16/06/05
Dans la même collection
-
Demain : quel temps ? Un mathématicien en visite chez Chronos
DESHOUILLERS Jean-Marc
Jean-Marc Deshouillers, professeur à l’Institut de mathématiques de Bordeaux, revient sur la conceptualisation scientifique du temps. Il démontre par le biais d’exemples concrets (Achille et la tortue
-
La théorie des cordes
BACHAS Costas
La théorie des supercordes propose d'unifier les quatre interactions fondamentales, en décrivant toutes les particules élémentaires comme des différents états de vibration d'une corde. Si les
-
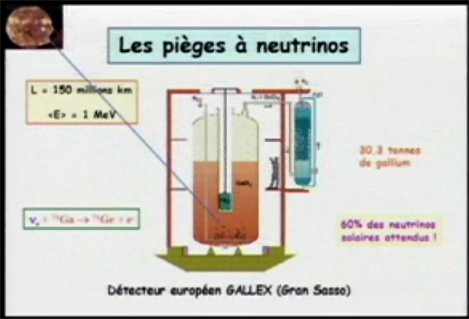
Les neutrinos dans l'Univers
VIGNAUD Daniel
Notre corps humain contient environ 20 millions de neutrinos issus du big bang, émet quelques milliers de neutrinos liés à sa radioactivité naturelle. Traversé en permanence par 65 milliards de
-
De l'atome au cristal : les propriétés électroniques des matériaux
GEORGES Antoine
Métaux, semi-conducteurs, ou même supraconducteurs transportant un courant électrique sans aucune résistance, les matériaux présentent une diversité de propriétés électroniques remarquable, mise à
-
Les condensats de Bose-Einstein
DALIBARD Jean
Le laser, outil privilégié du chirurgien et du soudeur, est souvent associé à l'idée de chaleur. Depuis une vingtaine d'années, on sait pourtant l'utiliser pour refroidir les atomes d'un gaz à une
-
La gravitation
DERUELLE Nathalie
Le terme gravitation a une origine relativement récente puisqu'il date du XVIIIème siècle : il a été inventé pour désigner une théorie qui jetait un pont entre les phénomènes terrestres et célestes.
-
Einstein aujourd'hui
BALIBAR Françoise
Parce qu'il est universellement célèbre, tout le monde croit connaître Einstein. Les physiciens, à cet égard, ne font pas exception à la règle. On va répétant à l'envie les mêmes lieux communs sur l
-
Physique et cosmologie
BOUCHET François
L'équipe scientifique du satellite WMAP a annoncé récemment les résultats très attendus de leur cartographie des anisotropies du fond de rayonnement cosmologique. Les caractéristiques de ce fond
-
La mécanique des fluides
MOFFATT Henry Keith
La dynamique des fluides est un sujet qui s'applique largement : en biologie, en géophysique et en astrophysique, en océanographie et en météorologie, ainsi qu'en génies chimique, nucléaire,
-
La physique quantique (Philippe Grangier)
GRANGIER Philippe
Nous décrirons des expériences permettant de mettre en évidence des propriétés simples et fondamentales de la physique quantique, comme l'existence de superpositions linéaires d'états, ou celle d
Avec les mêmes intervenants et intervenantes
-
Pourquoi la matière change-t-elle d'état : la compétition entre ordre et désordre
BRéZIN Édouard
"Les changements d'état de la matière, sous l'effet d'une élévation ou d'un abaissement de température, sont des phénomènes bien familiers. De même, on connaît depuis longtemps des substances dont la
Sur le même thème
-
ML-enhancement of simulation and optimization in electromagnetism
PESTOURIE Raphaël
Full-wave simulations of large-scale electromagnetic devices — spanning thousands of wavelengths while featuring sub-wavelength geometrical details — pose significant computational challenges….
-
Trou noir dans une baignoire
JACQUET Maxime
Faire des expériences dans lesquelles la lumière se comporte comme un fluide et l'utiliser pour étudier la physique des trous noirs.
-
Les ondes gravitationnelles et leurs applications
ARBEY Alexandre
Lors de ce séminaire, je présenterai la théorie de la gravitation selon Einstein et la nature des ondes gravitationnelles, et je discuterai de leurs applications présentes et futures.
-
"Le mathématicien Petre (Pierre) Sergescu, historien des sciences, personnalité du XXe siècle"
HERLéA Alexandre
Alexandre HERLEA est membre de la section « Sciences, histoire des sciences et des techniques et archéologie industrielle » du CTHS. Professeur émérite des universités, membre effectif de l'Académie
-
Webinaire sur la rédaction des PGD
LOUVET Violaine
Rédaction des Plans de Gestion de Données (PGD) sous l’angle des besoins de la communauté mathématique.
-
Alexandre Booms : « Usage de matériel pédagogique adapté en géométrie : une transposition à interro…
« Usage de matériel pédagogique adapté en géométrie : une transposition à interroger ». Alexandre Booms, doctorant (Université de Reims Champagne-Ardenne - Cérep UR 4692)
-
A. Mondino - Time-like Ricci curvature bounds via optimal transport
MONDINO Andrea
The goal of the talk is to present a recent work in collaboration with Cavalletti (SISSA) on optimal transport in Lorentzian synthetic spaces. The aim is to set up a “Lorentzian analog” of the
-
M. Lesourd - Positive Scalar Curvature on Noncompact Manifolds and the Positive Mass Theorem
LESOURD Martin
The study of positive scalar curvature on noncompact manifolds has seen significant progress in the last few years. A major role has been played by Gromov's results and conjectures, and in
-
R. Perales - Recent Intrinsic Flat Convergence Theorems
PERALES Raquel
Théorèmes récents de convergence plane intrinsèque
-
J. Fine - Knots, minimal surfaces and J-holomorphic curves
FINE Joël
I will describe work in progress, parts of which are joint with Marcelo Alves. Let L be a knot or link in the 3-sphere. I will explain how one can count minimal surfaces in hyperbolic 4-space
-
P. Burkhardt - Pointwise lower scalar curvature bounds for C0 metrics via regularizing Ricci flow
BURKHARDT-GUIM Paula
We propose a class of local definitions of weak lower scalar curvature bounds that is well defined for C0 metrics. We show the following: that our definitions are stable under greater-than-second
-
D. Semola - Boundary regularity and stability under lower Ricci bounds
SEMOLA Daniele
The theory of non smooth spaces with lower Ricci Curvature bounds has undergone huge developments in the last thirty years. On the one hand the impetus came from Gromov’s precompactness theorem