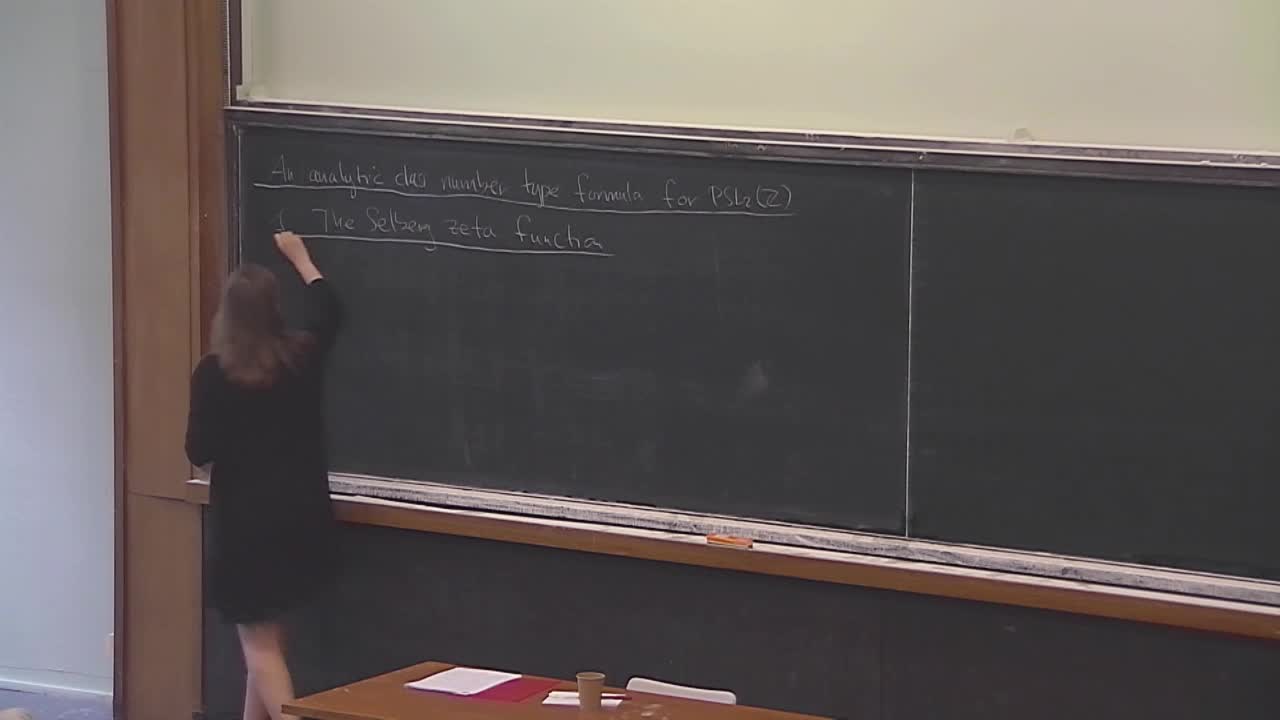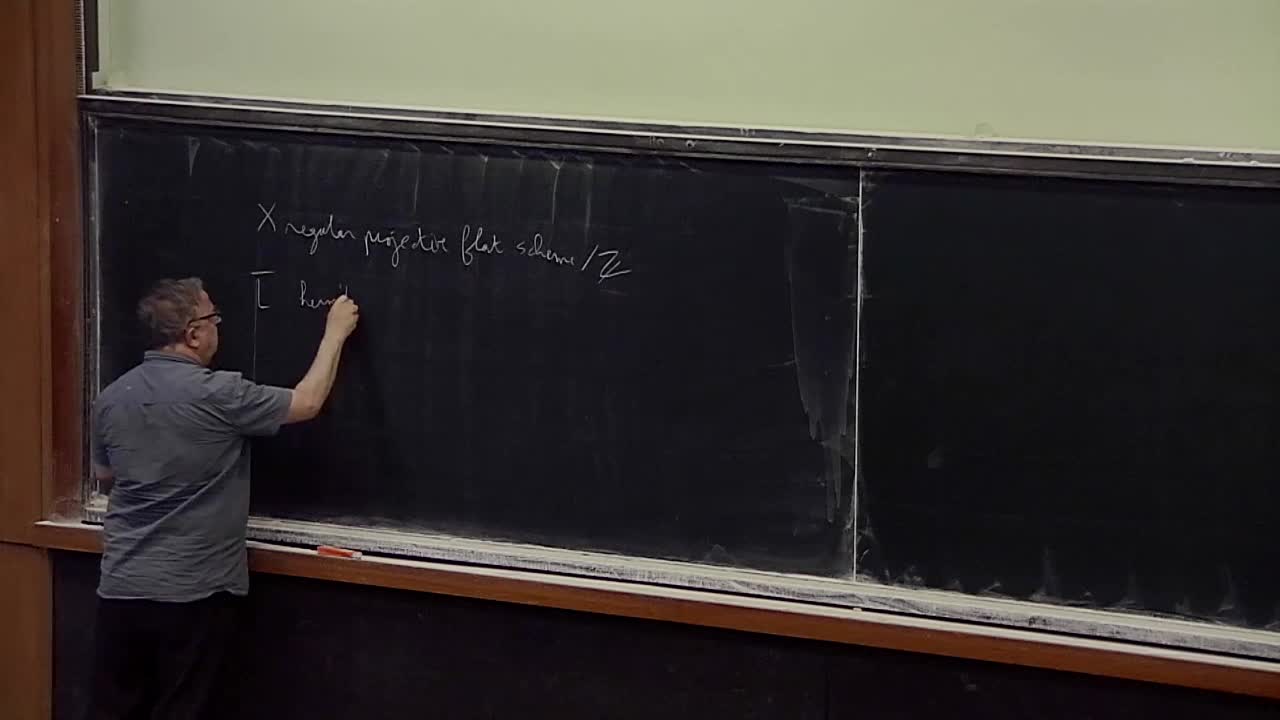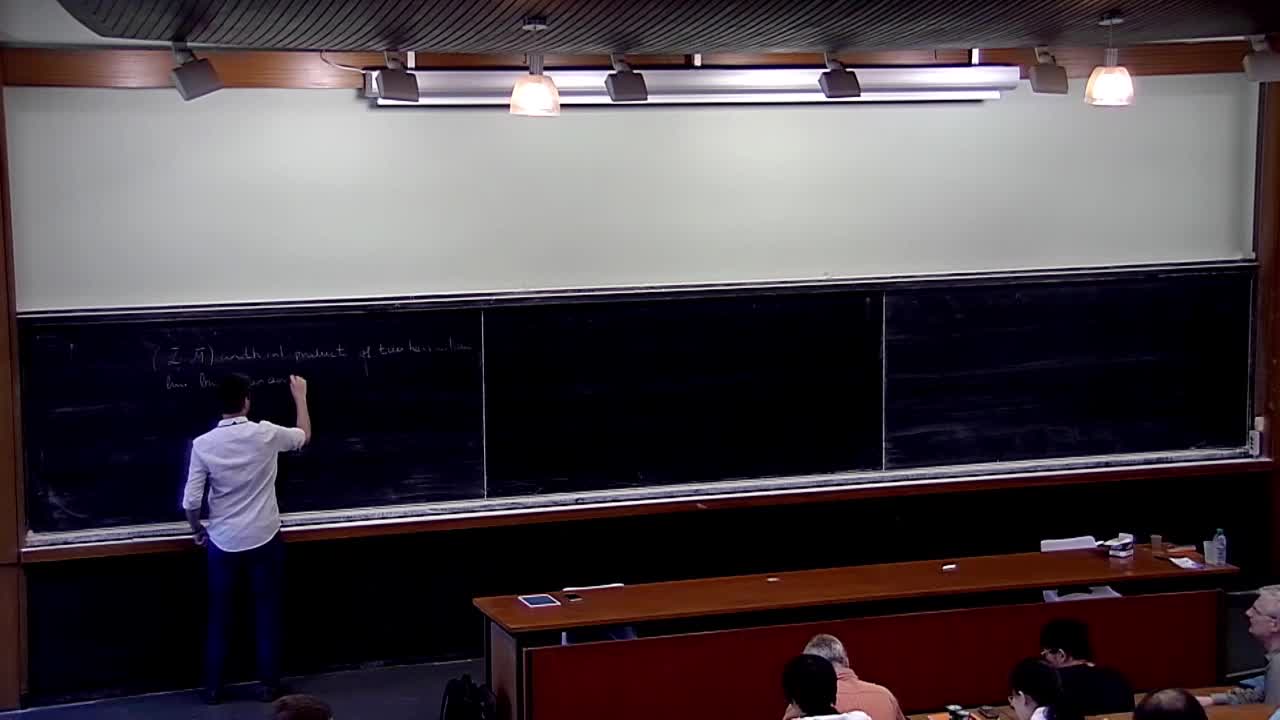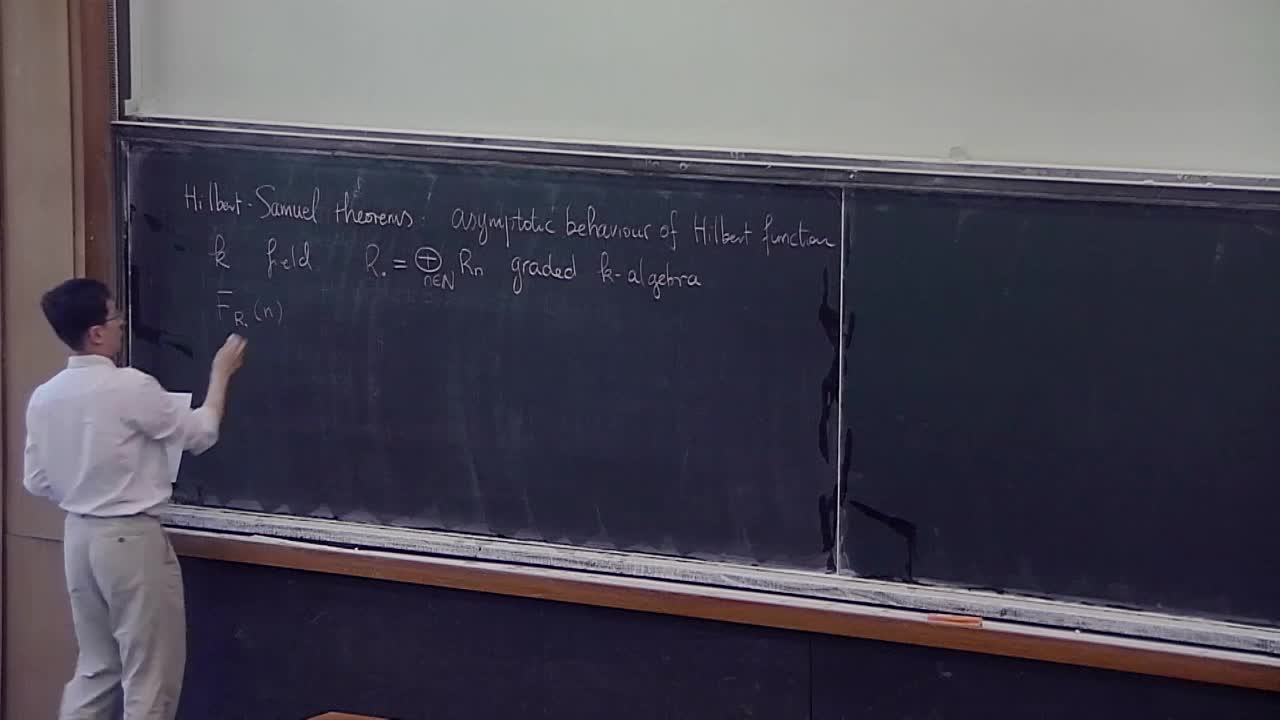2017

Vidéos
X. Yuan - On the arithmetic degree of Shimura curves
The goal of this talk is to introduce a Gross--Zagier type formula, which relates the arithmetic self-intersection number of the Hodge bundle of a quaternionic Shimura curve over a totally real
Y. Tang - Exceptional splitting of reductions of abelian surfaces with real multiplication
Chavdarov and Zywina showed that after passing to a suitable field extension, every abelian surface A with real multiplication over some number field has geometrically simple reduction modulo p
A. von Pippich - An analytic class number type formula for PSL2(Z)
For any Fuchsian subgroup Γ⊂PSL2(R) of the first kind, Selberg introduced the Selberg zeta function in analogy to the Riemann zeta function using the lengths of simple closed geodesics on Γ∖H
D. Loughran - Sieving rational points on algebraic varieties
Sieves are an important tool in analytic number theory. In a typical sieve problem, one is given a list of p-adic conditions for all primes p, and the challenge is to count the number of integers
Z. Huang - Diophantine approximation and local distribution of rational points
We show how to use the recent work of D. McKinnon and M. Roth on generalizations of Diophantine approximation to algebraic varieties to formulate a local version of the Batyrev-Manin principle on
C. Soulé - Arithmetic Intersection (Part4)
Let X be a 2-dimensional, normal, flat, proper scheme over the integers. Assume ¯L and ¯M are two hermitian line bundles over X. Arakelov (and Deligne) defined a real number ¯L.¯M, the arithmetic
C. Soulé - Arithmetic Intersection (Part3)
Let X be a 2-dimensional, normal, flat, proper scheme over the integers. Assume ¯L and ¯M are two hermitian line bundles over X. Arakelov (and Deligne) defined a real number ¯L.¯M, the arithmetic
C. Soulé - Arithmetic Intersection (Part2)
Let X be a 2-dimensional, normal, flat, proper scheme over the integers. Assume ¯L and ¯M are two hermitian line bundles over X. Arakelov (and Deligne) defined a real number ¯L.¯M, the arithmetic
C. Soulé - Arithmetic Intersection (Part1)
Let X be a 2-dimensional, normal, flat, proper scheme over the integers. Assume ¯L and ¯M are two hermitian line bundles over X. Arakelov (and Deligne) defined a real number ¯L.¯M, the arithmetic
P. Salberger - Quantitative aspects of rational points on algebraic varieties (part4)
Let X be a subvariety of Pn defined over a number field and N(B) be the number of rational points of height at most B on X. There are then general conjectures of Manin on the asymptotic behaviour
P. Salberger - Quantitative aspects of rational points on algebraic varieties (part3)
Let X be a subvariety of Pn defined over a number field and N(B) be the number of rational points of height at most B on X. There are then general conjectures of Manin on the asymptotic behaviour
P. Salberger - Quantitative aspects of rational points on algebraic varieties (part2)
Let X be a subvariety of Pn defined over a number field and N(B) be the number of rational points of height at most B on X. There are then general conjectures of Manin on the asymptotic behaviour
P. Salberger - Quantitative aspects of rational points on algebraic varieties (part1)
Let X be a subvariety of Pn defined over a number field and N(B) be the number of rational points of height at most B on X. There are then general conjectures of Manin on the asymptotic behaviour
E. Peyre - Slopes and distribution of points (part4)
The distribution of rational points of bounded height on algebraic varieties is far from uniform. Indeed the points tend to accumulate on thin subsets which are images of non-trivial finite
E. Peyre - Slopes and distribution of points (part3)
The distribution of rational points of bounded height on algebraic varieties is far from uniform. Indeed the points tend to accumulate on thin subsets which are images of non-trivial finite
E. Peyre - Slopes and distribution of points (part2)
The distribution of rational points of bounded height on algebraic varieties is far from uniform. Indeed the points tend to accumulate on thin subsets which are images of non-trivial finite
E. Peyre - Slopes and distribution of points (part1)
The distribution of rational points of bounded height on algebraic varieties is far from uniform. Indeed the points tend to accumulate on thin subsets which are images of non-trivial finite
É. Gaudron - Minima et pentes des espaces adéliques rigides (Part3)
Ce cours présente un abrégé de la théorie des minima et pentes successives des espaces adéliques rigides sur une extension algébrique du corps des nombres rationnels. Seront réunis dans un même
É. Gaudron - Minima et pentes des espaces adéliques rigides (Part 2)
Ce cours présente un abrégé de la théorie des minima et pentes successives des espaces adéliques rigides sur une extension algébrique du corps des nombres rationnels. Seront réunis dans un même
É. Gaudron - Minima et pentes des espaces adéliques rigides (Part1)
Ce cours présente un abrégé de la théorie des minima et pentes successives des espaces adéliques rigides sur une extension algébrique du corps des nombres rationnels. Seront réunis dans un même
G.Freixas i Montplet - Automorphic forms and arithmetic intersections (part 3)
In these lectures I will focus on the Riemann-Roch theorem in Arakelov geometry, in the specific context of some simple Shimura varieties. For suitable data, the cohomological part of the theorem
G. Freixas i Montplet - Automorphic forms and arithmetic intersections (part 2)
In these lectures I will focus on the Riemann-Roch theorem in Arakelov geometry, in the specific context of some simple Shimura varieties. For suitable data, the cohomological part of the theorem
R. Dujardin - Some problems of arithmetic origin in complex dynamics and geometry (part3)
Some themes inspired from number theory have been playing an important role in holomorphic and algebraic dynamics (iteration of rational mappings) in the past ten years. In these lectures I would
R. Dujardin - Some problems of arithmetic origin in complex dynamics and geometry (part2)
Some themes inspired from number theory have been playing an important role in holomorphic and algebraic dynamics (iteration of rational mappings) in the past ten years. In these lectures I would
R. Dujardin - Some problems of arithmetic origin in complex dynamics and geometry (part1)
Some themes inspired from number theory have been playing an important role in holomorphic and algebraic dynamics (iteration of rational mappings) in the past ten years. In these lectures I would
H.Chen - Théorème de Hilbert-Samuel arithmétique (Part3)
Le théorème de Hilbert-Samuel en géométrie algébrique relie le comportement asymptotique du système linéaire gradué d’un faisceau inversible ample au nombre d’intersection. Gillet et Soulé ont
H. Chen - Théorème de Hilbert-Samuel arithmétique (Part2)
Le théorème de Hilbert-Samuel en géométrie algébrique relie le comportement asymptotique du système linéaire gradué d’un faisceau inversible ample au nombre d’intersection. Gillet et Soulé ont
H. Chen - Théorème de Hilbert-Samuel arithmétique (Part1)
Le théorème de Hilbert-Samuel en géométrie algébrique relie le comportement asymptotique du système linéaire gradué d’un faisceau inversible ample au nombre d’intersection. Gillet et Soulé ont
A. Chambert-Loir - Equidistribution theorems in Arakelov geometry and Bogomolov conjecture (part4)
Let X be an algebraic curve of genus g⩾2 embedded in its Jacobian variety J. The Manin-Mumford conjecture (proved by Raynaud) asserts that X contains only finitely many points of finite order.
A. Chambert-Loir - Equidistribution theorems in Arakelov geometry and Bogomolov conjecture (part3)
Let X be an algebraic curve of genus g⩾2 embedded in its Jacobian variety J. The Manin-Mumford conjecture (proved by Raynaud) asserts that X contains only finitely many points of finite order.
A. Chambert-Loir - Equidistribution theorems in Arakelov geometry and Bogomolov conjecture (part2)
Let X be an algebraic curve of genus g⩾2 embedded in its Jacobian variety J. The Manin-Mumford conjecture (proved by Raynaud) asserts that X contains only finitely many points of finite order.
A. Chambert-Loir - Equidistribution theorems in Arakelov geometry and Bogomolov conjecture (part1)
Let X be an algebraic curve of genus g⩾2 embedded in its Jacobian variety J. The Manin-Mumford conjecture (proved by Raynaud) asserts that X contains only finitely many points of finite order.
J. Bruinier et J. Ignacio Burgos Gil - Arakelov theory on Shimura varieties (part2)
A Shimura variety is a higher-dimensional analogue of a modular curve that arises as a quotient of a Hermitian symmetric space by a congruence subgroup of a reductive algebraic group defined over
J. Bruinier et J. Ignacio Burgos Gil - Arakelov theory on Shimura varieties (part1)
A Shimura variety is a higher-dimensional analogue of a modular curve that arises as a quotient of a Hermitian symmetric space by a congruence subgroup of a reductive algebraic group defined over
J-B Bost - Theta series, infinite rank Hermitian vector bundles, Diophantine algebraization (Part2)
In the classical analogy between number fields and function fields, an Euclidean lattice (E,∥.∥) may be seen as the counterpart of a vector bundle V on a smooth projective curve C over some field
J-B Bost - Theta series, infinite rank Hermitian vector bundles, Diophantine algebraization (Part1)
In the classical analogy between number fields and function fields, an Euclidean lattice (E,∥.∥) may be seen as the counterpart of a vector bundle V on a smooth projective curve C over some field
F. Andreatta - The height of CM points on orthogonal Shimura varieties and Colmez conjecture (part5)
We will first introduce Shimura varieties of orthogonal type, their Heegner divisors and some special points, called CM (Complex Multiplication) points. Secondly we will review conjectures of
F. Andreatta - The height of CM points on orthogonal Shimura varieties and Colmez conjecture (part4)
We will first introduce Shimura varieties of orthogonal type, their Heegner divisors and some special points, called CM (Complex Multiplication) points. Secondly we will review conjectures of
F. Andreatta - The height of CM points on orthogonal Shimura varieties and Colmez conjecture (part3)
We will first introduce Shimura varieties of orthogonal type, their Heegner divisors and some special points, called CM (Complex Multiplication) points. Secondly we will review conjectures of
F. Andreatta - The height of CM points on orthogonal Shimura varieties and Colmez conjecture (part2)
We will first introduce Shimura varieties of orthogonal type, their Heegner divisors and some special points, called CM (Complex Multiplication) points. Secondly we will review conjectures of
F. Andreatta - The height of CM points on orthogonal Shimura varieties and Colmez conjecture (part1)
We will first introduce Shimura varieties of orthogonal type, their Heegner divisors and some special points, called CM (Complex Multiplication) points. Secondly we will review conjectures of
Intervenants et intervenantes
Mathématicien. En poste : Département de mathématiques "Federigo Enriques", Milan, Italie (en 2016)
Mathématicien. Professeur au département de mathématiques dans l’équipe d’arithmétique et géométrie algébrique de l’Université Paris-Sud, Orsay, Essonne, depuis 1998
Mathématicien. En poste : Mathematical institute, University of Heidelberg, Allemagne (en 2002)
En poste : Fachbereich Mathematik, Technische Universität Darmstadt, Allemagne (en 2020)
Mathématicien. Chercheur à l'Instituto de Ciencias Matemáticas – ICMAT, Madrid (en 2021).
Rapporteur d'une thèse de : Mathématiques, Université Paris-Sud 11, Orsay (en 2011)
Agrégé de mathématiques
Écrit aussi en anglais
Mathématicien. En poste à l'IRMAR, Université de Rennes 1 (en 2005). Professeur en poste à l'université Paris-Diderot (Paris 7), UFR de mathématiques, Institut de mathématiques de Jussieu—Paris Rive Gauche (équipe de topologie et géométrie algébriques), Paris, France en 2018
mathématicien. Professeur des universités, à l'Université Grenoble Alpes de 2012 à 2016 ; et depuis 2016, à l'Institut de Mathématiques de Jussieu - Paris Rive Gauche, Université Paris Diderot - Paris 7 (en 2019)
Professeur de mathématiques à Sorbonne université, Paris (en 2025). Membre de l'UMR 8001 - Laboratoire de Probabilités, Statistique et Modélisation (LPSM)
Auteur d'une thèse de : Mathématiques, Université Paris 11, Orsay (en 2002). En poste à l'Ecole polytechnique (en 2011)
Auteur d'une thèse de : mathématiques, Université Paris-Sud 11, Orsay (en 2007)
Mathématicien. En poste à : Institut de Mathématiques de Jussieu, Paris, France (en 2019)
Titulaire d'un doctorat d'université en Mathématiques (Saint-Etienne, 2001)
En poste à l'université Grenoble I, Institut Fourier, UMR 5582 (CNRS), 38402 Saint-Martin-D'Hères (en 2005)
En poste au laboratoire de Mathématiques Blaise Pascal de l'Université Clermont Auvergne (en 2017).
Auteur d'une thèse en Mathématiques à Grenoble Alpes en 2017
Lecturer in Pure Mathematica, University of Bath (en 2021)
Professeur de mathématiques à l'Institut de Recherche Mathématique Avancée, Université Louis Pasteur et C.N.R.S., Strasbourg (en 1998), directeur de thèse à l'Université Joseph Fourier de Grenoble, en poste au laboratoire de mathématiques (en 2003).
Professeur à l'Institut Fourier, Université Grenoble Alpes (en 2025)
Mathématicienne. En poste à la Technische Universität Darmstadt (en 2017)
Rapporteur d'une thèse en Mathématiques à Paris 11 et professeur de Mathématiques. Professeur de mathématiques, Chalmers University of Technology and University of Gothenburg (Suède) en 2019
Titulaire d'un doctorat en Mathématiques à l'université Paris 7, 1978. Mathématicien.
Directeur de recherche CNRS à l’IHES. Professeur émérite depuis 2017
Mathématicienne. Titulaire d'un doctorat de mathématiques de l'université d'Harvard (2017)