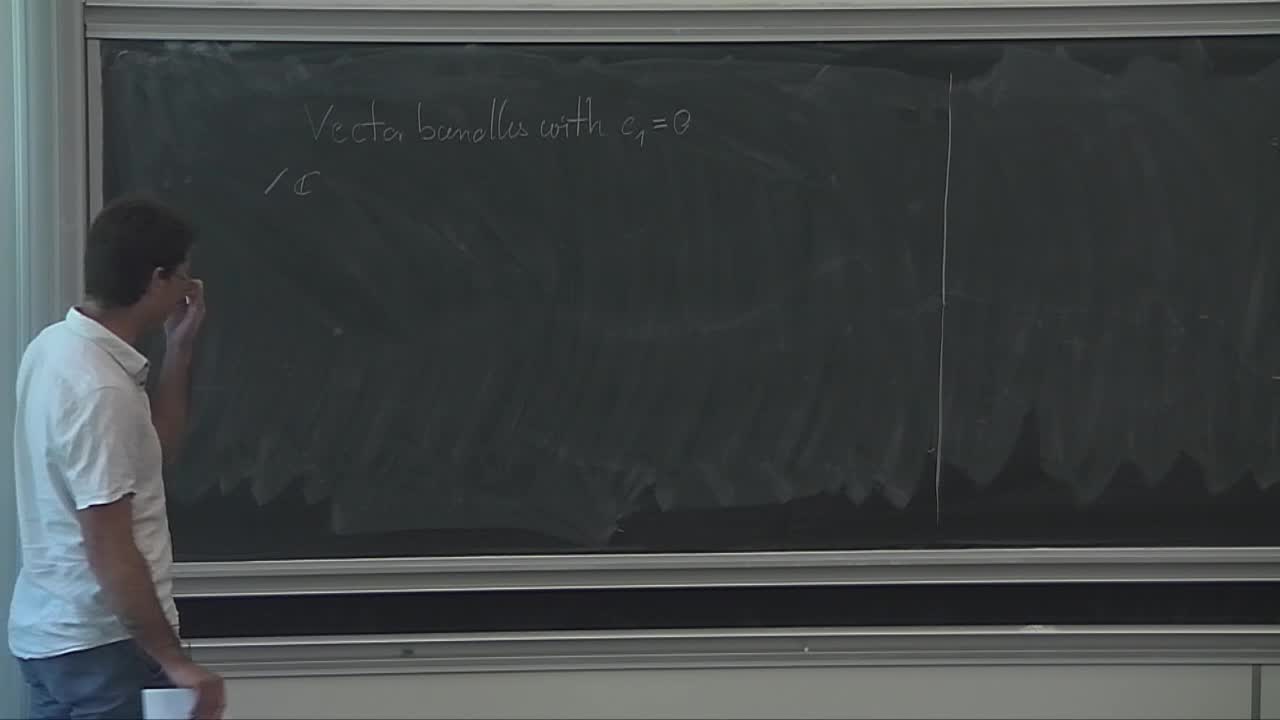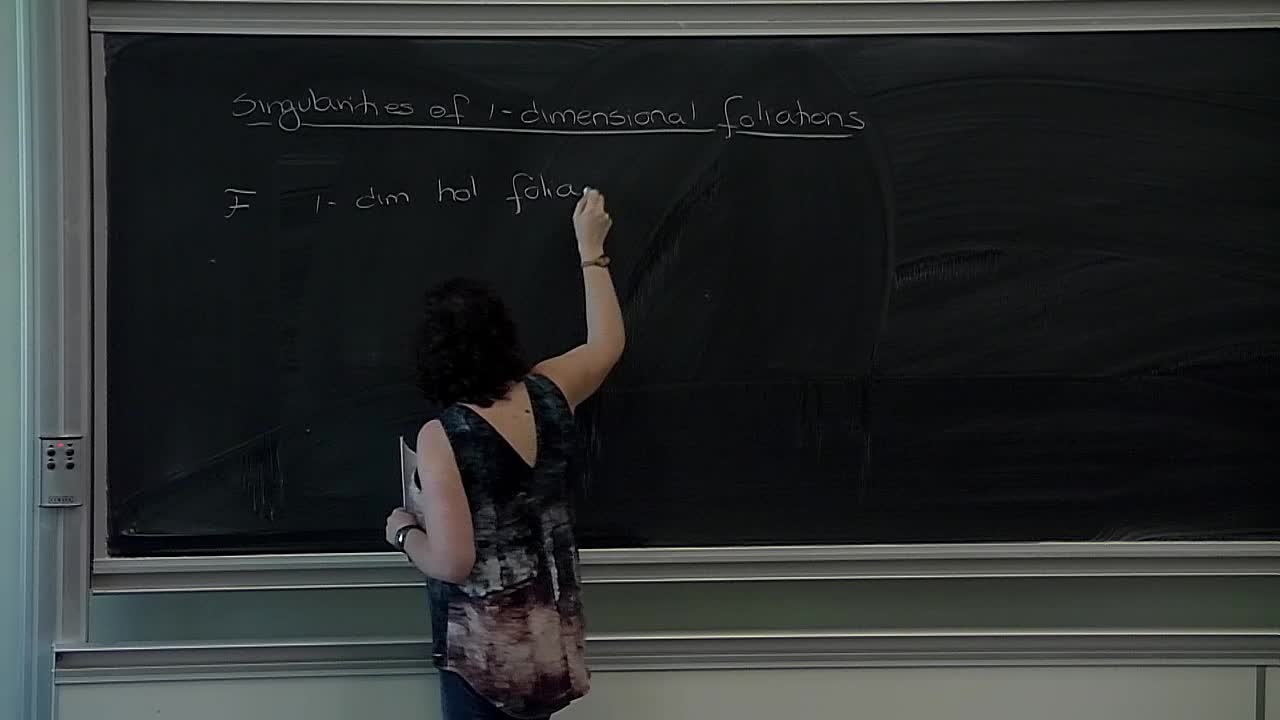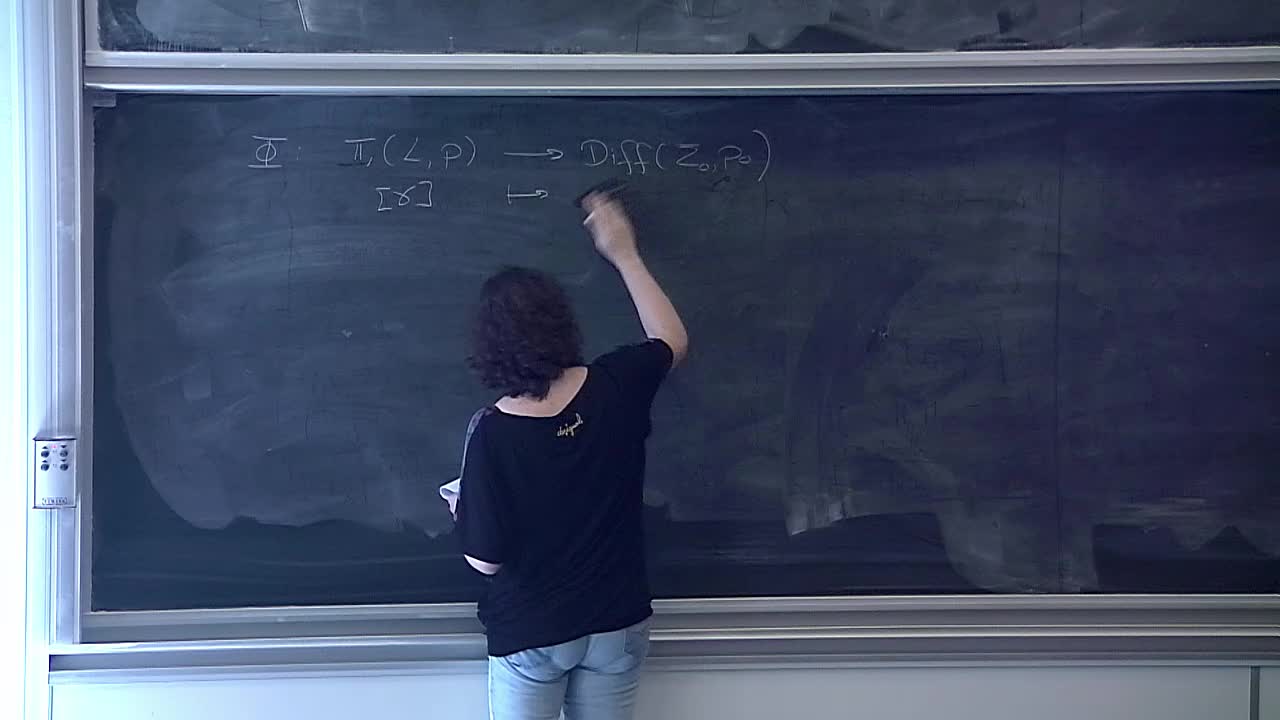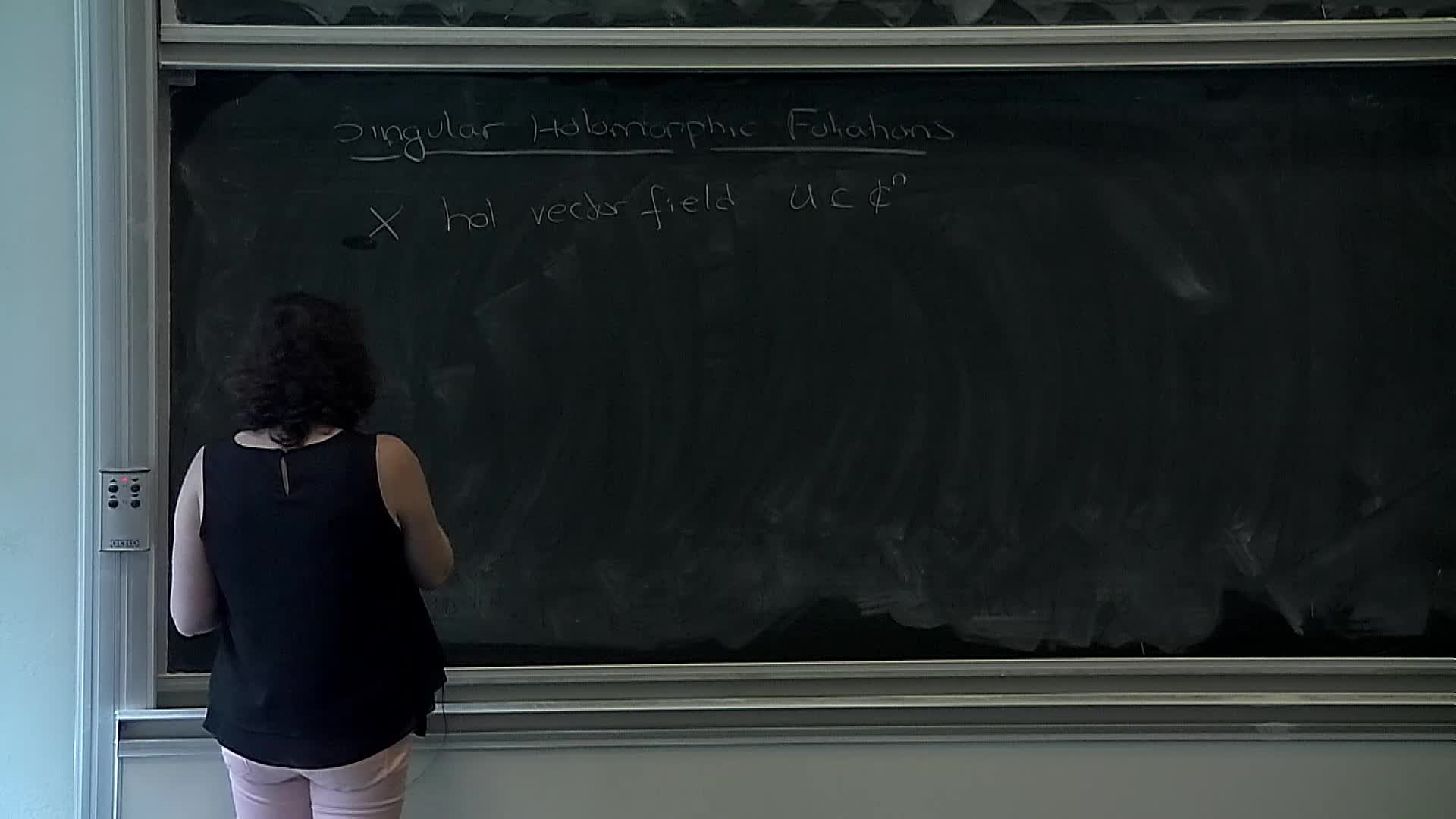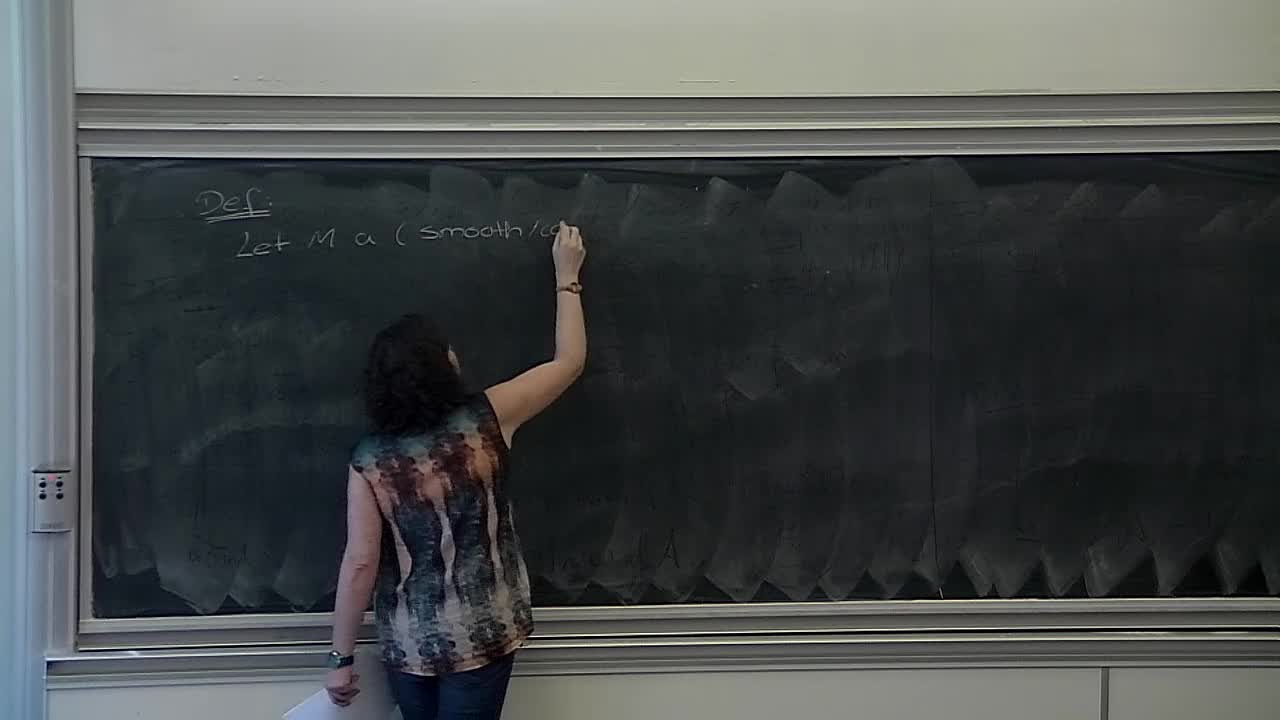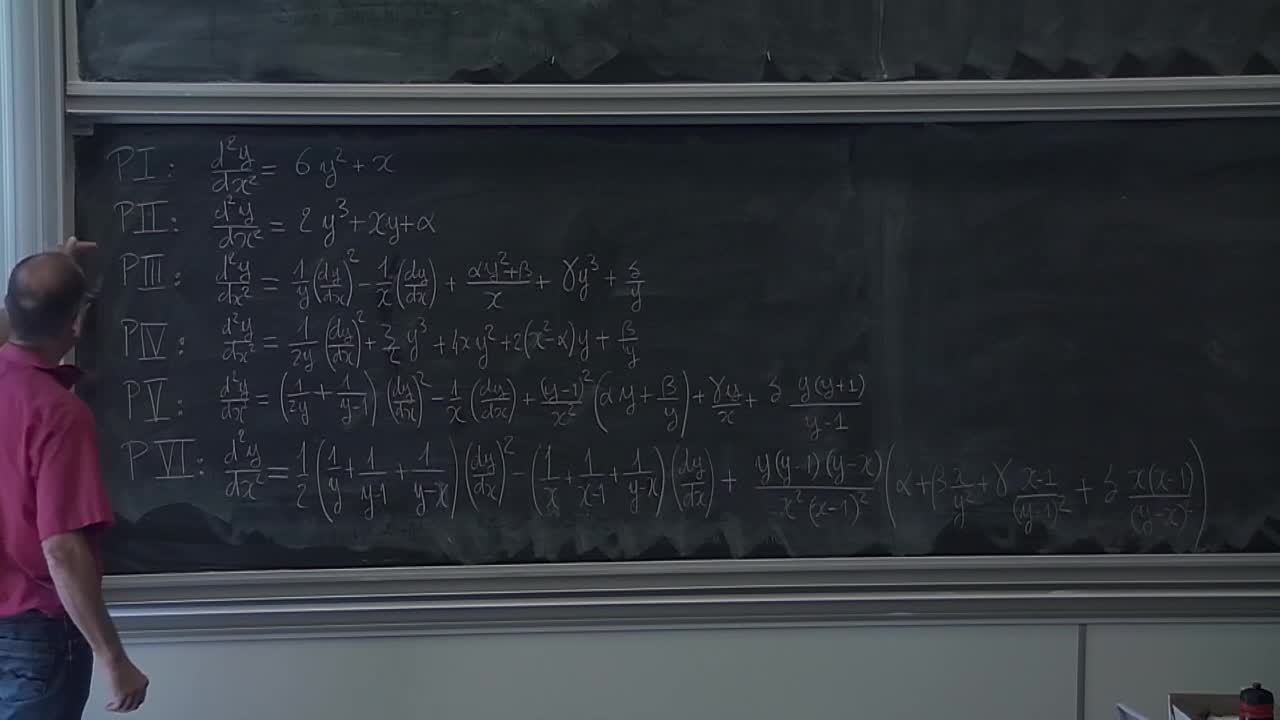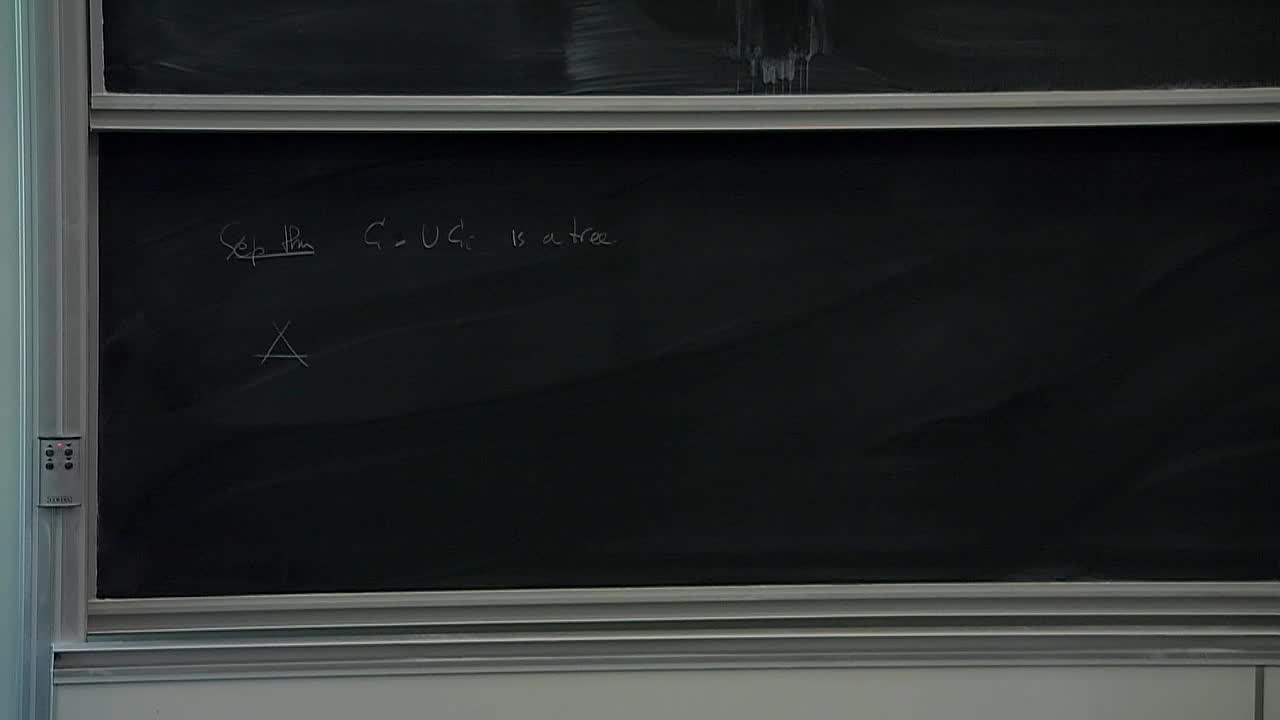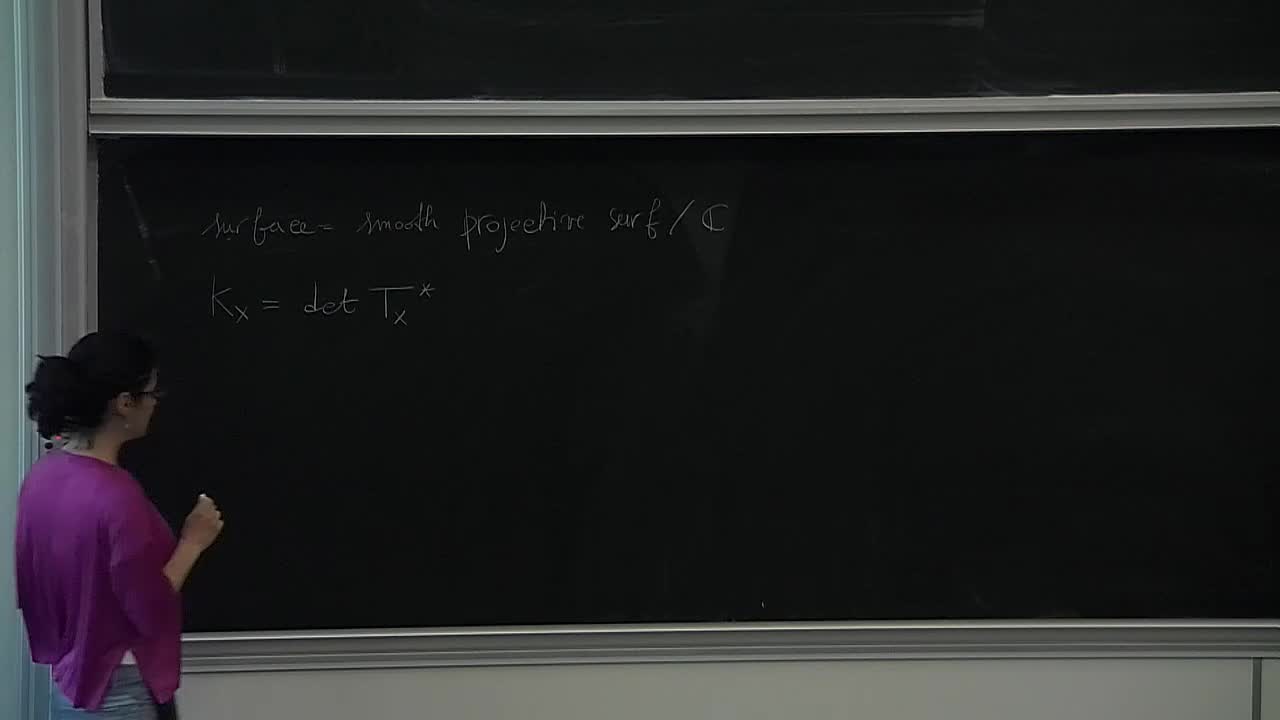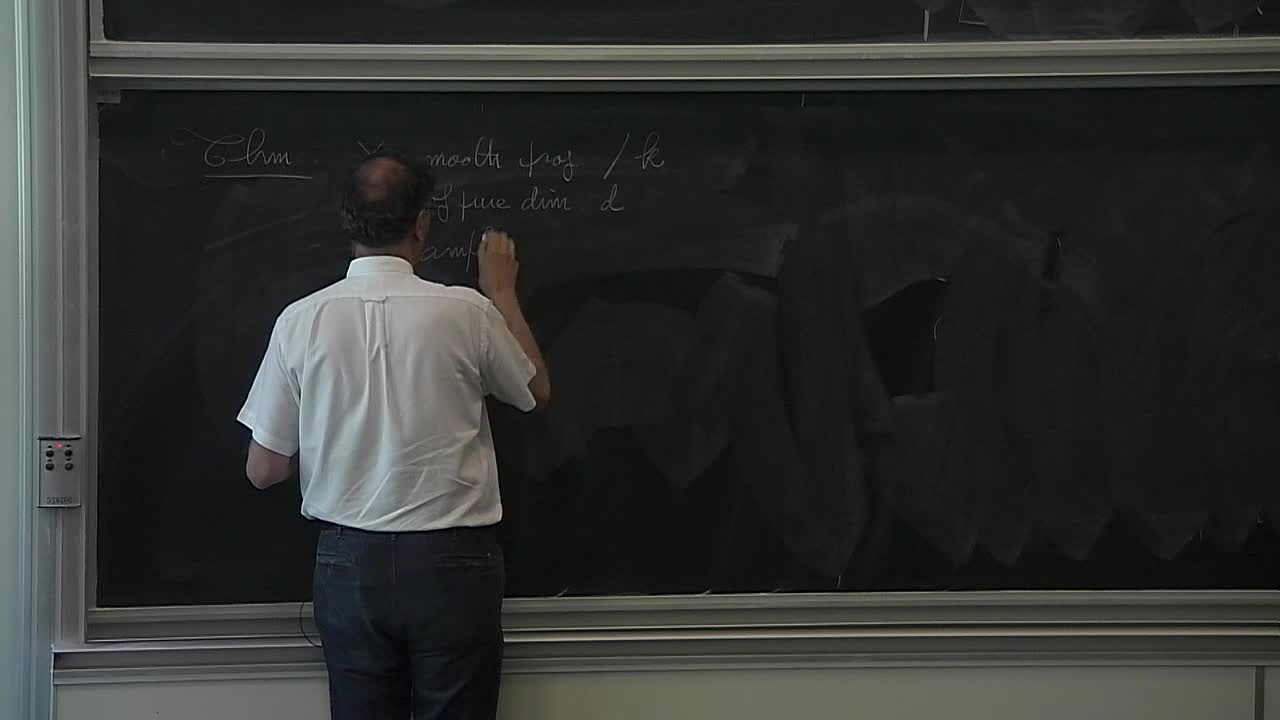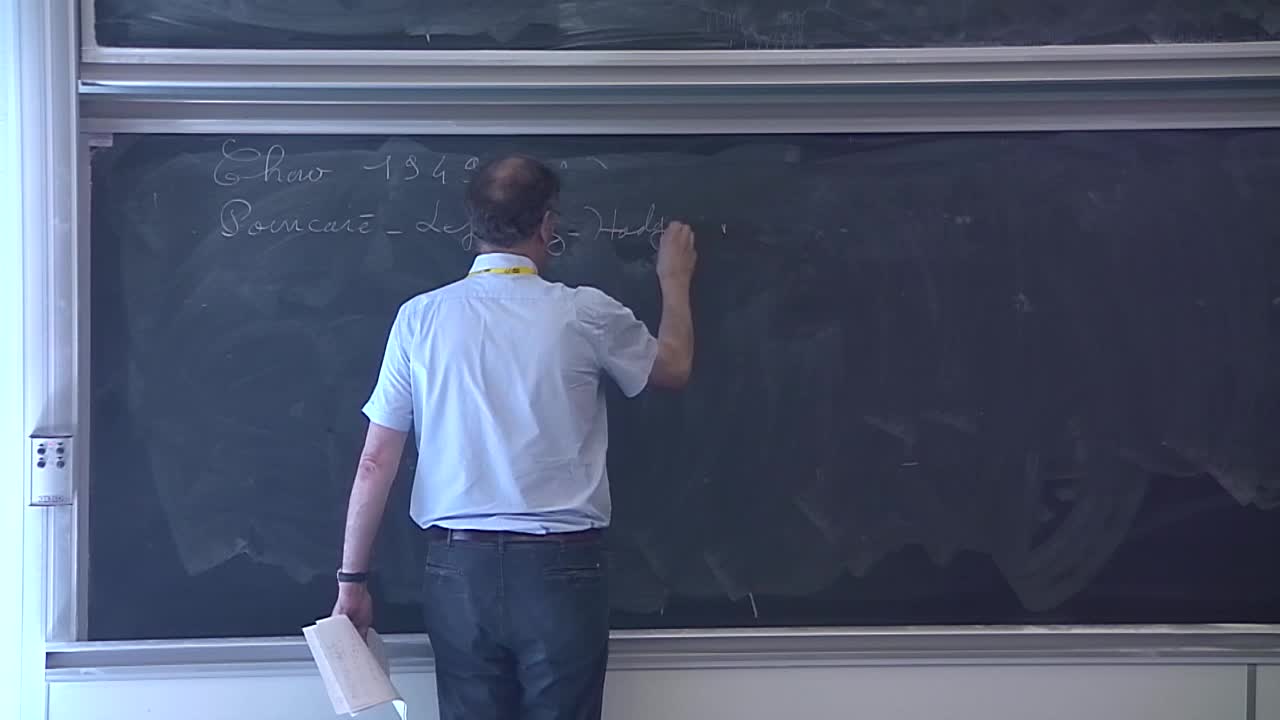2019
Vidéos
H. Guenancia - A decomposition theorem for singular spaces with trivial canonical class (Part 2)
The Beauville-Bogomolov decomposition theorem asserts that any compact Kähler manifold with numerically trivial canonical bundle admits an étale cover that decomposes into a product of a torus, an
A. Höring - A decomposition theorem for singular spaces with trivial canonical class (Part 3)
The Beauville-Bogomolov decomposition theorem asserts that any compact Kähler manifold with numerically trivial canonical bundle admits an étale cover that decomposes into a product of a torus, an
S. Druel - A decomposition theorem for singular spaces with trivial canonical class (Part 5)
The Beauville-Bogomolov decomposition theorem asserts that any compact Kähler manifold with numerically trivial canonical bundle admits an étale cover that decomposes into a product of a torus, an
F. Touzet - About the analytic classification of two dimensional neighborhoods of elliptic curves
I will investigate the analytic classification of two dimensional neighborhoods of an elliptic curve C with trivial normal bundle and discuss the existence of foliations having C as a leaf. Joint work
C. Spicer - Minimal models of foliations
We will discuss some recent work on the minimal model program (MMP) for foliations and explain some applications of the MMP to the study of foliation singularities and to the study of some
D. Novikov - Wilkie's conjecture for restricted elementary functions
We consider the structure $\mathbb{R}^{RE}$ obtained from $(\mathbb{R},
L. Meersseman - Kuranishi and Teichmüller
Let X be a compact complex manifold. The Kuranishi space of X is an analytic space which encodes every small deformation of X. The Teichmüller space is a topological space formed by the classes
S. Ghazouani - Isoholonomic foliations of moduli spaces of Riemann surfaces
In this talk, I will introduce families of foliations on the moduli space of Riemann surfaces M_{g,n} which we call Veech foliations. These foliations are defined by identifying M_{g,n} to
B. Deroin - The Jouanolou foliation
I will discuss dynamical properties of the Jouanolou foliation of the complex projective plane in degree two. Joint work with Aurélien Alvarez.
J. Demailly - Existence of logarithmic and orbifold jet differentials
Given a projective algebraic orbifold, one can define associated logarithmic and orbifold jet bundles. These bundles describe the algebraic differential operators that act on germs of curves
G. Binyamini - Point counting for foliations over number fields
We consider an algebraic $V$ variety and its foliation, both defined over a number field. Given a (compact piece of a) leaf $L$ of the foliation, and a subvariety $W$ of complementary
A. Belotto da Silva - Singular foliations in sub-Riemannian geometry and the Strong Sard Conjecture
Given a totally nonholonomic distribution of rank two $\Delta$ on a three-dimensional manifold $M$, it is natural to investigate the size of the set of points $\mathcal{X}^x$ that can be reached
E. Amerik - On the characteristic foliation
Let X be a holomorphic symplectic manifold and D a smooth hypersurface in X. Then the restriction of the symplectic form on D has one-dimensional kernel at each point. This distribution is
S. Druel - A decomposition theorem for singular spaces with trivial canonical class (Part 4)
The Beauville-Bogomolov decomposition theorem asserts that any compact Kähler manifold with numerically trivial canonical bundle admits an étale cover that decomposes into a product of a torus,
H. Guenancia - A decomposition theorem for singular spaces with trivial canonical class (Part 1)
The Beauville-Bogomolov decomposition theorem asserts that any compact Kähler manifold with numerically trivial canonical bundle admits an étale cover that decomposes into a product of a torus,
H. Reis - Introduction to holomorphic foliations (Part 4)
The purpose of this course is to present the basics of the general theory of (singular) holomorphic foliations. We will begin with the general definition of a (regular) foliation and its
H. Reis - Introduction to holomorphic foliations (Part 3)
The purpose of this course is to present the basics of the general theory of (singular) holomorphic foliations. We will begin with the general definition of a (regular) foliation and its
H. Reis - Introduction to holomorphic foliations (Part 2)
The purpose of this course is to present the basics of the general theory of (singular) holomorphic foliations. We will begin with the general definition of a (regular) foliation and its
H. Reis - Introduction to holomorphic foliations (Part 1)
The purpose of this course is to present the basics of the general theory of (singular) holomorphic foliations. We will begin with the general definition of a (regular) foliation and its
F. Polizzi - Classification of surfaces via Mori theory (Part 4)
We give a summary of the Minimal Model Program (namely, Mori Theory) in the case of surfaces.
F. Polizzi - Classification of surfaces via Mori theory (Part 3)
We give a summary of the Minimal Model Program (namely, Mori Theory) in the case of surfaces.
F. Polizzi - Classification of surfaces via Mori theory (Part 2)
We give a summary of the Minimal Model Program (namely, Mori Theory) in the case of surfaces.
F. Polizzi - Classification of surfaces via Mori theory (Part 1)
We give a summary of the Minimal Model Program (namely, Mori Theory) in the case of surfaces.
J.-V. Pereira - Algebraic leaves of codimension one foliations (Part 4)
This mini-course will review old and new results about algebraic leaves of codimension one foliations on projective manifolds. I will discuss some of the following topics: Darboux's Theorem and
J.-V. Pereira - Algebraic leaves of codimension one foliations (Part 3)
This mini-course will review old and new results about algebraic leaves of codimension one foliations on projective manifolds. I will discuss some of the following topics: Darboux's Theorem and
J. V. Pereira - Algebraic leaves of codimension one foliations (Part 2)
This mini-course will review old and new results about algebraic leaves of codimension one foliations on projective manifolds. I will discuss some of the following topics: Darboux's Theorem and
J. V. Pereira - Algebraic leaves of codimension one foliations (Part 1)
This mini-course will review old and new results about algebraic leaves of codimension one foliations on projective manifolds. I will discuss some of the following topics: Darboux's Theorem and
F. Loray - Painlevé equations and isomonodromic deformations II (Part 4)
In these lectures, we use the material of V. Heu and H. Reis' lectures to introduce and study Painlevé equations from the isomonodromic point of view. The main objects are rank 2 systems of
F. Loray - Painlevé equations and isomonodromic deformations II (Part 3)
In these lectures, we use the material of V. Heu and H. Reis' lectures to introduce and study Painlevé equations from the isomonodromic point of view. The main objects are rank 2 systems of linear
F. Loray - Painlevé equations and isomonodromic deformations II (Part 2)
In these lectures, we use the material of V. Heu and H. Reis' lectures to introduce and study Painlevé equations from the isomonodromic point of view. The main objects are rank 2 systems of
F. Loray - Painlevé equations and isomonodromic deformations II (Part 1)
In these lectures, we use the material of V. Heu and H. Reis' lectures to introduce and study Painlevé equations from the isomonodromic point of view. The main objects are rank 2 systems of
C. Gasbarri - Techniques d’algébrisation en géométrie analytique, formelle, et diophantienne I (Par…
Dans ce cours, nous nous proposons d’expliquer comment des théorèmes d’algébrisation classiques, concernant des variétés ou des faisceux cohérents analytiques, possèdent des avatars en géométrie
C. Gasbarri - Techniques d’algébrisation en géométrie analytique, formelle, et diophantienne I (Par…
Dans ce cours, nous nous proposons d’expliquer comment des théorèmes d’algébrisation classiques, concernant des variétés ou des faisceux cohérents analytiques, possèdent des avatars en géométrie
C. Gasbarri - Techniques d’algébrisation en géométrie analytique, formelle, et diophantienne I (Par…
Dans ce cours, nous nous proposons d’expliquer comment des théorèmes d’algébrisation classiques, concernant des variétés ou des faisceux cohérents analytiques, possèdent des avatars en géométrie
C. Gasbarri - Techniques d’algébrisation en géométrie analytique, formelle, et diophantienne I (Par…
Dans ce cours, nous nous proposons d’expliquer comment des théorèmes d’algébrisation classiques, concernant des variétés ou des faisceux cohérents analytiques, possèdent des avatars en géométrie
E. Floris - Birational geometry of foliations on surfaces (Part 4)
The goal of this minicourse is to introduce MMP for foliations on surfaces and to outline the classification of foliations on projective surfaces up to birational equivalence.
E. Floris - Birational geometry of foliations on surfaces (Part 3)
The goal of this minicourse is to introduce MMP for foliations on surfaces and to outline the classification of foliations on projective surfaces up to birational equivalence.
E. Floris - Birational geometry of foliations on surfaces (Part 2)
The goal of this minicourse is to introduce MMP for foliations on surfaces and to outline the classification of foliations on projective surfaces up to birational equivalence.
E. Floris - Birational geometry of foliations on surfaces (Part 1)
The goal of this minicourse is to introduce MMP for foliations on surfaces and to outline the classification of foliations on projective surfaces up to birational equivalence.
S. Diverio - Kobayashi hyperbolicity of complex projective manifolds and foliations (Part 4)
The aim of this mini course is to highlight some links between the study of the Kobayashi hyperbolicity properties of complex projective manifolds and holomorphic foliations. A compact
S. Diverio - Kobayashi hyperbolicity of complex projective manifolds and foliations (Part 3)
The aim of this mini course is to highlight some links between the study of the Kobayashi hyperbolicity properties of complex projective manifolds and holomorphic foliations. A compact
S. Diverio - Kobayashi hyperbolicity of complex projective manifolds and foliations (Part 2)
The aim of this mini course is to highlight some links between the study of the Kobayashi hyperbolicity properties of complex projective manifolds and holomorphic foliations. A compact
S. Diverio - Kobayashi hyperbolicity of complex projective manifolds and foliations (part 1)
The aim of this mini course is to highlight some links between the study of the Kobayashi hyperbolicity properties of complex projective manifolds and holomorphic foliations. A compact
J.-B. Bost - Techniques d’algébrisation en géométrie analytique, formelle, et diophantienne II (Par…
Dans ce cours, nous nous proposons d’expliquer comment des théorèmes d’algébrisation classiques, concernant des variétés ou des faisceux cohérents analytiques, possèdent des avatars en géométrie
J.-B. Bost - Techniques d’algébrisation en géométrie analytique, formelle, et diophantienne II (Par…
Dans ce cours, nous nous proposons d’expliquer comment des théorèmes d’algébrisation classiques, concernant des variétés ou des faisceux cohérents analytiques, possèdent des avatars en géométrie
J.-B. Bost - Techniques d’algébrisation en géométrie analytique, formelle, et diophantienne II (Par…
Dans ce cours, nous nous proposons d’expliquer comment des théorèmes d’algébrisation classiques, concernant des variétés ou des faisceux cohérents analytiques, possèdent des avatars en géométrie
J.-B. Bost - Techniques d’algébrisation en géométrie analytique, formelle, et diophantienne II (Par…
Dans ce cours, nous nous proposons d’expliquer comment des théorèmes d’algébrisation classiques, concernant des variétés ou des faisceux cohérents analytiques, possèdent des avatars en géométrie
C. Araujo - Foliations and birational geometry (Part 4)
In the last few decades, much progress has been made in birational algebraic geometry. The general viewpoint is that complex projective manifolds should be classified according to the behavior
C. Araujo - Foliations and birational geometry (Part 3)
In the last few decades, much progress has been made in birational algebraic geometry. The general viewpoint is that complex projective manifolds should be classified according to the behavior
C. Araujo - Foliations and birational geometry (Part 2)
In the last few decades, much progress has been made in birational algebraic geometry. The general viewpoint is that complex projective manifolds should be classified according to the behavior
C. Araujo - Foliations and birational geometry (Part 1)
In the last few decades, much progress has been made in birational algebraic geometry. The general viewpoint is that complex projective manifolds should be classified according to the behavior
Intervenants et intervenantes
Professeur à l'Université Paris-Saclay (en 2021)
Auteur d'une thèse en Mathématiques à Mulhouse en 2013. Professeur des Université, Université Paris Cité (en 2023)
Rapporteur d'une thèse en mathématiques soutenue à Grenoble (en 2018)
Mathématicien. Professeur au département de mathématiques dans l’équipe d’arithmétique et géométrie algébrique de l’Université Paris-Sud, Orsay, Essonne, depuis 1998
Mathématicien. - Ancien élève de l'École Normale Supérieure de Paris. - Auteur d'une thèse de 3e cycle à l'université de Paris 6 en 1978 et d'une thèse de doctorat d'État de mathématiques à Paris 6 en 1982. - Professeur de mathématiques pures à l'université de Grenoble 1 (1987-2013-). - Membre de jurys de thèses ou directeur de thèses
Chargé de recherche, Mathématiques - Université Paris Sud (Orsay)
Directeur de recherche à l'université de Cergy-Pontoise (en 2023)
Directeur d'une thèse de : mathématiques, Université Paris-Sud 11, Orsay (en 2011)
Président du jury d'une thèse en Mathématiques à Université Côte d'Azur en 2025
Titulaire d'un doctorat de l'Université Joseph Fourier de Grenoble, spécialité "Mathématiques"
Professeur à l'Université de Rome la Sapienza, au département de mathématiques Guido Catelnuovo
Auteur d'une thèse de doctorat en Mathématiques à Paris 11 (en 2000)
Chercheur CNRS affilié à l'Institut Fourier (en 2005). Directeur de thèse à l'Université de Grenoble (en 2015). Directeur de recherche CNRS, membre de l'Institut Camille Jordan, Université Claude Bernard, président de l'épi-comité épiMaths, sur Episciences (en 2023)
Auteur d'une thèse en Mathématiques à Strasbourg en 2013
Maîtresse de conférences à l'Université de Poitiers (en 2023)
Mathématicien. En poste à l'université Tor Vergata de Rome (en 2010). Professeur de mathématiques à l'université de Strasbourg, à l'Institut de recherche mathématique avancée (IRMA) (depuis 2009)
Docteur de PSL en Mathématiques (en 2017)
Mathématicien. Travaille à Mathematics Institute, Zeeman Building, University of Warwick Coventry, GB (en 2020)
Auteur d’une thèse de doctorat en mathématiques soutenue en 2013 à l'Université Pierre et Marie Curie, Paris
Titulaire d'un doctorat de l'Université Joseph Fourier de Grenoble, spécialité "Mathématiques"
Mathématicien. Professeur, Université Nice Sophia-Antipolis (en 2018). Professeur des universités, laboratoire J. A. Dieudonné, Université Côte d'Azur (en 2021)
Ecrit également sous le pseudonyme collectif Henri Paul de Saint-Gervais
Directeur de recherche à l'université de Rennes 1 (en 2023)
En poste à L'IRMAR (Rennes) (depuis 2002)
Chargé de recherche CNRS, laboratoire d'Arithmétique-Géométrie-Analyse-Topologie, université des sciences et technologies de Lille (1994-2002)
Maître de conférences en mathématiques à Rennes 1 (en 2004). Enseignant-chercheur en mathématiques à l'Université de Bourgogne
Docteur en Sciences (ingénierie)
Professeur au département de mathématiques et d'informatique de l'université de Calabre (Italie). Examinateur d'une thèse en Mathématiques à Aix-Marseille en 2018
Mathématicienne. Enseigne à l'Université de Porto (2019)
Mathématicien, Enseigne au King's College à Londres (2019)
Titulaire d'un doctorat en mathématiques et applications à Rennes 1 en 1995. Maître de conférences à Rennes 1 (en 2019)