Notice
J. V. Pereira - Algebraic leaves of codimension one foliations (Part 2)
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
This mini-course will review old and new results about algebraic leaves of codimension one foliations on projective manifolds. I will discuss some of the following topics: Darboux's Theorem and generalizations; compact leaves; holonomy of an algebraic leaf; and effective algebraic integration (a.k.a. Poincaré and Painlevé problems).
Intervention / Responsable scientifique
Thème
Documentation
Dans la même collection
-
H. Guenancia - A decomposition theorem for singular spaces with trivial canonical class (Part 2)
GuenanciaHenriThe Beauville-Bogomolov decomposition theorem asserts that any compact Kähler manifold with numerically trivial canonical bundle admits an étale cover that decomposes into a product of a torus, an
-
F. Touzet - About the analytic classification of two dimensional neighborhoods of elliptic curves
TouzetFrédéricI will investigate the analytic classification of two dimensional neighborhoods of an elliptic curve C with trivial normal bundle and discuss the existence of foliations having C as a leaf. Joint work
-
A. Höring - A decomposition theorem for singular spaces with trivial canonical class (Part 3)
HöringAndreasThe Beauville-Bogomolov decomposition theorem asserts that any compact Kähler manifold with numerically trivial canonical bundle admits an étale cover that decomposes into a product of a torus, an
-
C. Spicer - Minimal models of foliations
SpicerCalumWe will discuss some recent work on the minimal model program (MMP) for foliations and explain some applications of the MMP to the study of foliation singularities and to the study of some
-
S. Druel - A decomposition theorem for singular spaces with trivial canonical class (Part 5)
DruelStéphaneThe Beauville-Bogomolov decomposition theorem asserts that any compact Kähler manifold with numerically trivial canonical bundle admits an étale cover that decomposes into a product of a torus, an
-
D. Novikov - Wilkie's conjecture for restricted elementary functions
NovikovDmitriĭ AleksandrovichWe consider the structure $\mathbb{R}^{RE}$ obtained from $(\mathbb{R},
-
B. Deroin - The Jouanolou foliation
DeroinBertrandI will discuss dynamical properties of the Jouanolou foliation of the complex projective plane in degree two. Joint work with Aurélien Alvarez.
-
A. Belotto da Silva - Singular foliations in sub-Riemannian geometry and the Strong Sard Conjecture
Belotto Da SilvaAndré RicardoGiven a totally nonholonomic distribution of rank two $\Delta$ on a three-dimensional manifold $M$, it is natural to investigate the size of the set of points $\mathcal{X}^x$ that can be reached
-
L. Meersseman - Kuranishi and Teichmüller
MeerssemanLaurentLet X be a compact complex manifold. The Kuranishi space of X is an analytic space which encodes every small deformation of X. The Teichmüller space is a topological space formed by the classes
-
J. Demailly - Existence of logarithmic and orbifold jet differentials
DemaillyJean-PierreGiven a projective algebraic orbifold, one can define associated logarithmic and orbifold jet bundles. These bundles describe the algebraic differential operators that act on germs of curves
-
E. Amerik - On the characteristic foliation
AmerikEkaterinaLet X be a holomorphic symplectic manifold and D a smooth hypersurface in X. Then the restriction of the symplectic form on D has one-dimensional kernel at each point. This distribution is
-
S. Ghazouani - Isoholonomic foliations of moduli spaces of Riemann surfaces
GhazouaniSelimIn this talk, I will introduce families of foliations on the moduli space of Riemann surfaces M_{g,n} which we call Veech foliations. These foliations are defined by identifying M_{g,n} to
Avec les mêmes intervenants et intervenantes
-
J.-V. Pereira - Algebraic leaves of codimension one foliations (Part 3)
PereiraJorge VitórioThis mini-course will review old and new results about algebraic leaves of codimension one foliations on projective manifolds. I will discuss some of the following topics: Darboux's Theorem and
-
J.-V. Pereira - Algebraic leaves of codimension one foliations (Part 4)
PereiraJorge VitórioThis mini-course will review old and new results about algebraic leaves of codimension one foliations on projective manifolds. I will discuss some of the following topics: Darboux's Theorem and
-
J. V. Pereira - Algebraic leaves of codimension one foliations (Part 1)
PereiraJorge VitórioThis mini-course will review old and new results about algebraic leaves of codimension one foliations on projective manifolds. I will discuss some of the following topics: Darboux's Theorem and
Sur le même thème
-
Tuan Ta Pesao : écritures de sable et de ficelle à l'Ile d'Ambrym
VandendriesscheEricCe film se déroule au Nord de l’île d’Ambrym, dans l’archipel de Vanuatu, en Mélanésie...
-
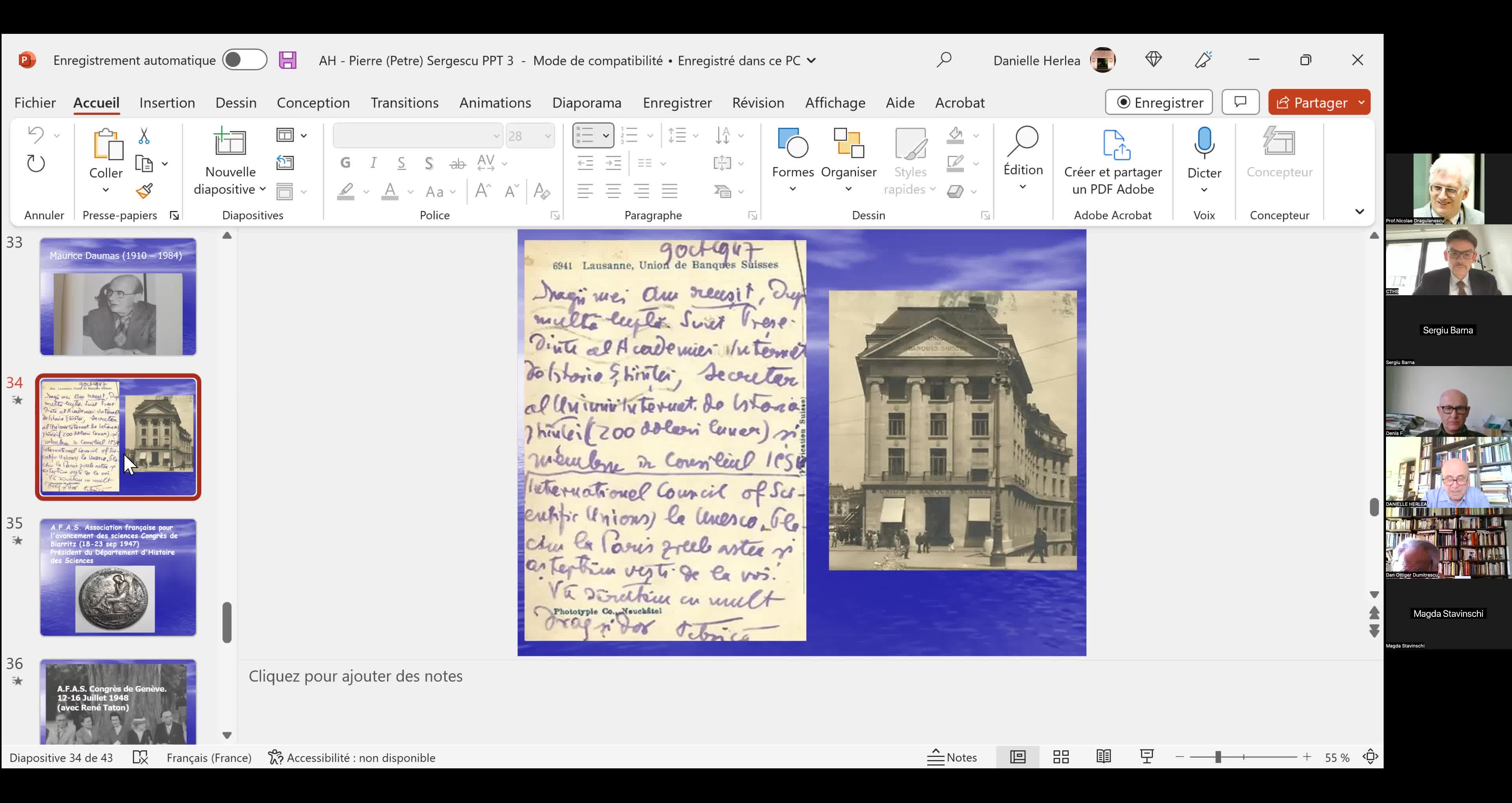
"Le mathématicien Petre (Pierre) Sergescu, historien des sciences, personnalité du XXe siècle"
HerléaAlexandreAlexandre HERLEA est membre de la section « Sciences, histoire des sciences et des techniques et archéologie industrielle » du CTHS. Professeur émérite des universités, membre effectif de l'Académie
-
Webinaire sur la rédaction des PGD
LouvetViolaineRédaction des Plans de Gestion de Données (PGD) sous l’angle des besoins de la communauté mathématique.
-
Alexandre Booms : « Usage de matériel pédagogique adapté en géométrie : une transposition à interro…
« Usage de matériel pédagogique adapté en géométrie : une transposition à interroger ». Alexandre Booms, doctorant (Université de Reims Champagne-Ardenne - Cérep UR 4692)
-
P. Burkhardt - Pointwise lower scalar curvature bounds for C0 metrics via regularizing Ricci flow
Burkhardt-GuimPaulaWe propose a class of local definitions of weak lower scalar curvature bounds that is well defined for C0 metrics. We show the following: that our definitions are stable under greater-than-second
-
R. Perales - Recent Intrinsic Flat Convergence Theorems
PeralesRaquelThéorèmes récents de convergence plane intrinsèque
-
J. Fine - Knots, minimal surfaces and J-holomorphic curves
FineJoëlI will describe work in progress, parts of which are joint with Marcelo Alves. Let L be a knot or link in the 3-sphere. I will explain how one can count minimal surfaces in hyperbolic 4-space
-
D. Semola - Boundary regularity and stability under lower Ricci bounds
SemolaDanieleThe theory of non smooth spaces with lower Ricci Curvature bounds has undergone huge developments in the last thirty years. On the one hand the impetus came from Gromov’s precompactness theorem
-
Y. Lai - A family of 3d steady gradient Ricci solitons that are flying wings
LaiYiWe find a family of 3d steady gradient Ricci solitons that are flying wings. This verifies a conjecture by Hamilton. For a 3d flying wing, we show that the scalar curvature does not vanish at
-
D. Stern - Harmonic map methods in spectral geometry
SternDanielOver the last fifty years, the problem of finding sharp upper bounds for area-normalized Laplacian eigenvalues on closed surfaces has attracted the attention of many geometers, due in part to
-
R. Bamler - Compactness and partial regularity theory of Ricci flows in higher dimensions
BamlerRichard H.We present a new compactness theory of Ricci flows. This theory states that any sequence of Ricci flows that is pointed in an appropriate sense, subsequentially converges to a synthetic flow.
-
C. Li - Classifying sufficiently connected PSC manifolds in 4 and 5 dimensions
LiChaoIn this talk, I will discuss some recent developments on the topology of closed manifolds admitting Riemannian metrics of positive scalar curvature. In particular, we will prove if a closed PSC