4. Comparaison de séquences

Descriptif
Au sommaire de cette quatrième partie :
4.1. Comment prédire les fonctions des gènes/protéines ?
4.2. Évolution et similarité de séquences
4.3. Quantifier la similarité de deux séquences
4.4. L'alignement de séquences devient un problème d'optimisation
4.5. Un alignement de séquences vu comme un chemin dans une grille
4.6. Si un chemin est optimal, tous ses chemins partiels sont optimaux
4.7. Coûts et alignement
4.8. Un algorithme récursif
4.9. Eviter la récursivité : une version itérative
4.10. Cet algorithme est-il efficace ?
Vidéos
4.1. Comment prédire les fonctions des gènes/protéines ?
Après avoir regardé dans les yeux, les semaines précédentes, l'ADN, vu comment cet ADN par séquençage produisait des textes, des séquences génomiques, étudié la relation entre gènes et protéines,
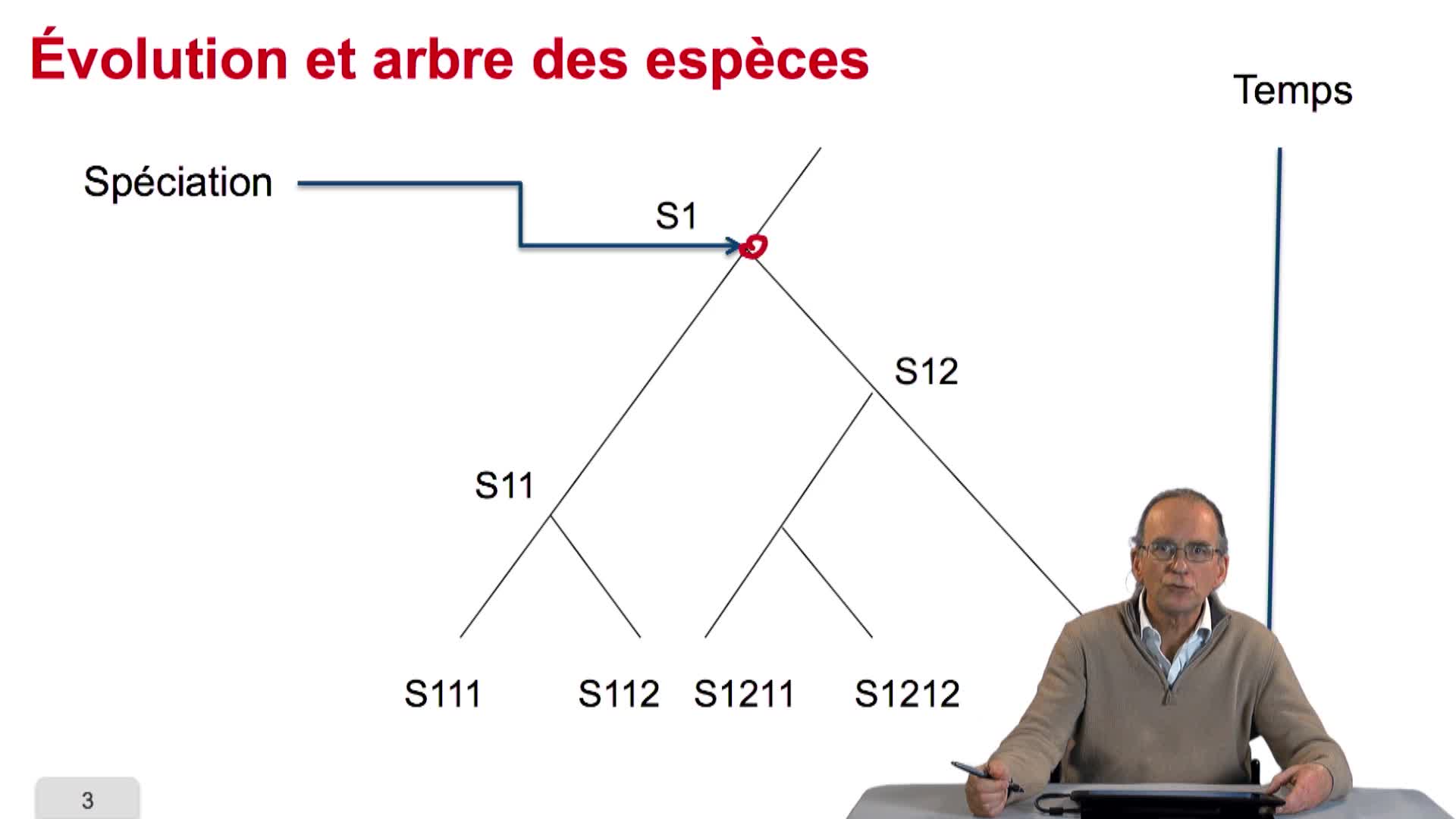
4.2. Évolution et similarité de séquences
Avant de chercher à quantifier ce qu'est la similarité de séquence, on peut se poser la question même de savoir pourquoi des séquences de génome sont similaires entre organismes. La réponse tient dans
4.3. Quantifier la similarité de deux séquences
Le principe est donc de rechercher, dans les bases de données, des séquences similaires à celles que nous sommes en train d'étudier. Nous faisons aussi l'hypothèse que plus les séquences sont
4.4. L’alignement de séquences devient un problème d’optimisation
La distance de Hamming nous donne une première possibilité de mesurer la similarité entre 2 séquences. Mais elle ne reflète pas suffisamment la réalité biologique. Qu'est-ce que j'entends par là ? On
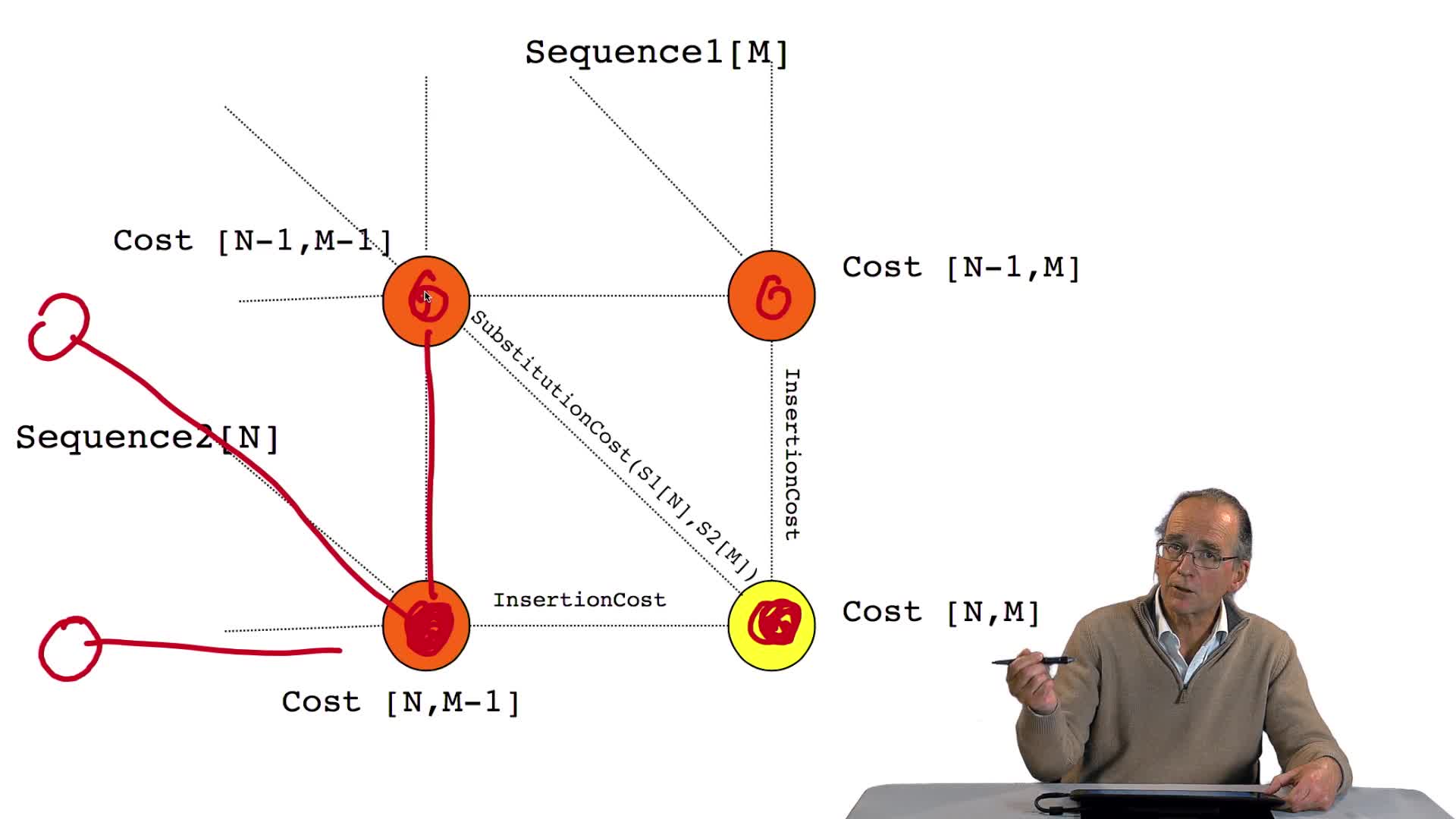
4.5. Un alignement de séquences vu comme un chemin dans une grille
Pour comparer deux séquences entre elles, il faut donc les aligner. Aligner ces deux séquences suppose faire des hypothèses d'insertion, délétion, aux bons endroits. Ça signifie, d'un point de vue
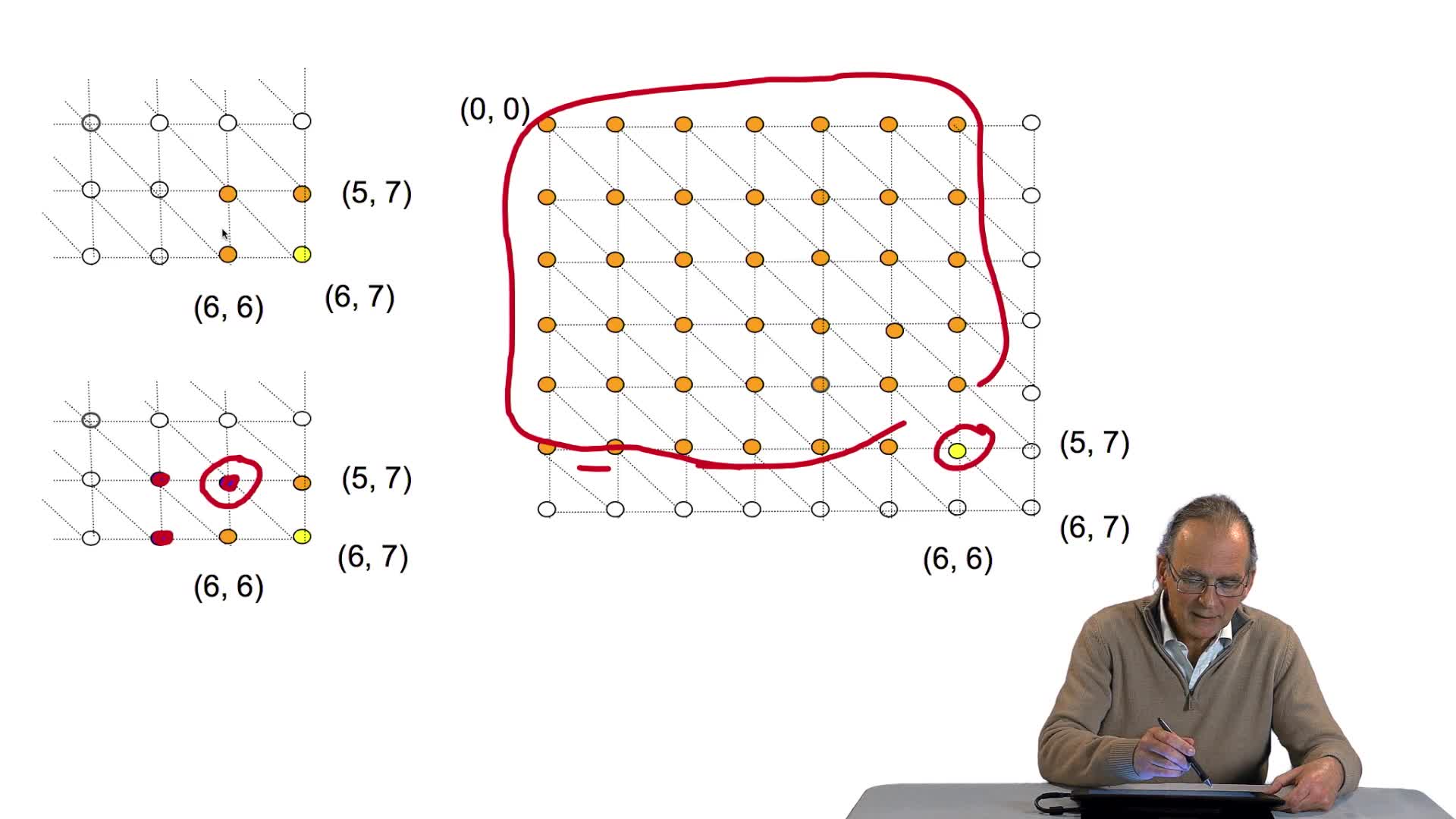
4.6. Si un chemin est optimal, tous ses chemins partiels sont optimaux
Nous cherchons à concevoir un algorithme capable de déterminer l'alignement optimal de 2 séquences. Et nous avons vu que ça revient à chercher un algorithme qui recherche un chemin optimal dans une
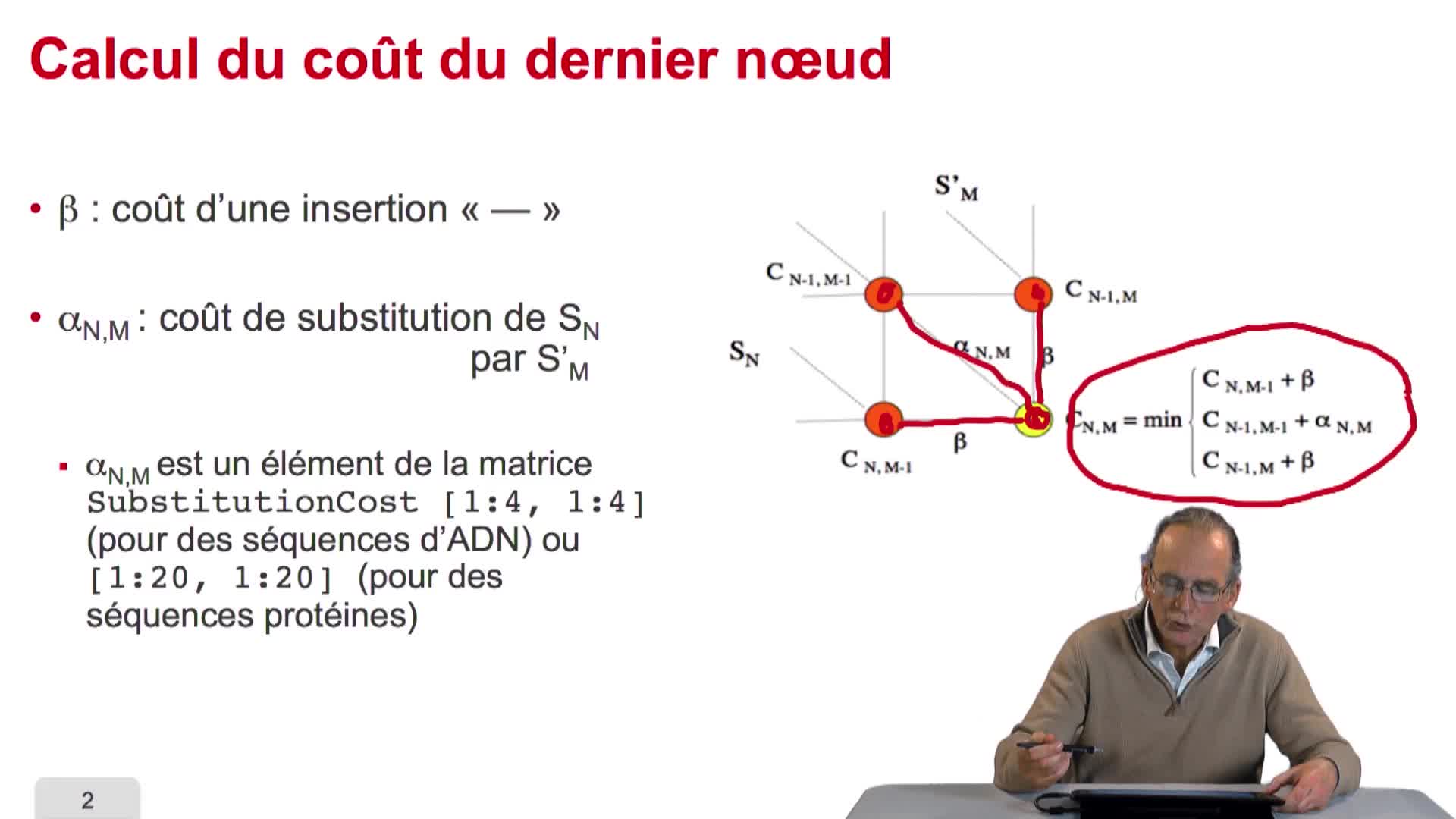
4.7. Coûts et alignement
Nous avons vu l'ébauche de notre algorithme d'alignement optimal en considérant la possibilité de calculer le coût optimal, ou score optimal, de ce dernier noeud. Et nous avons vu que le coût de ce
4.8. Un algorithme récursif
Nous avons désormais en main tous les éléments pour écrire notre algorithme de détermination d'un alignement optimal, ici d'un chemin optimal. Avec les notations que nous avons introduites, je vous
4.9. Éviter la récursivité : une version itérative
La fonction récursive que nous avons obtenue est d'un code assez compact et plutôt élégant, mais effectivement peu efficace. Pourquoi ? Rappelons son fonctionnement. Cette fonction est d'abord appelée
4.10. Cet algorithme est-il efficace ?
La version itérative de notre algorithme d'alignement optimal de séquences est indéniablement beaucoup plus efficace que sa version récursive, puisque nous avons vu qu'il permettait d'éviter que le
Intervenants et intervenantes
Ingénieur de recherche chez Inria. Exepert du langage de programmation Python (2015)
Ingénieur. Auteur d'une thèse de docteur-ingénieur en sciences appliquées (Grenoble INPG, 1976). - HDR. Directeur de thèse à Grenoble INPG (1990-1994-) et à l'université de Grenoble 1. Directeur de recherche au centre Inria Grenoble – Rhône-Alpes (2002, 2015)