Notice
4.6. Si un chemin est optimal, tous ses chemins partiels sont optimaux
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
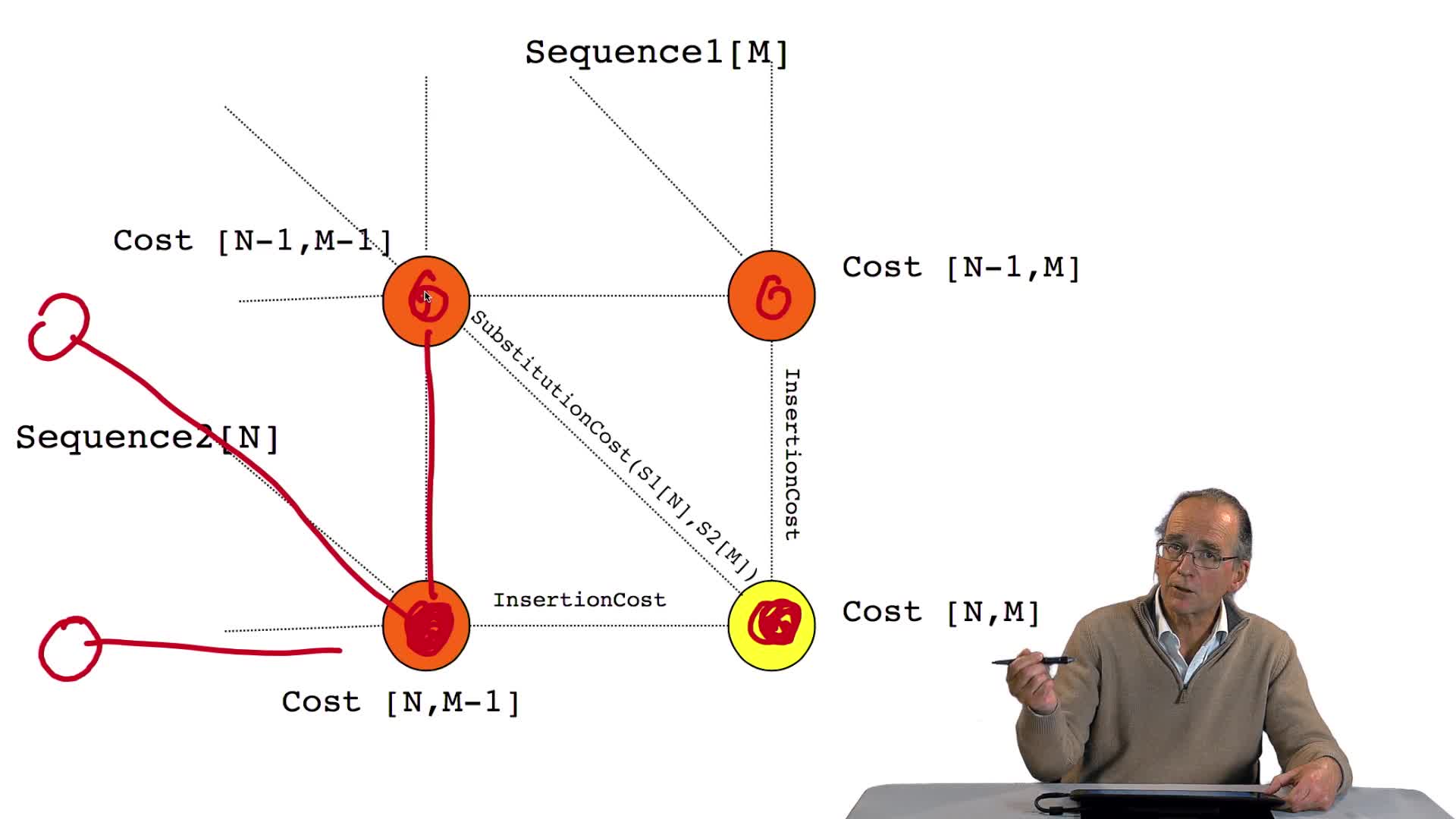
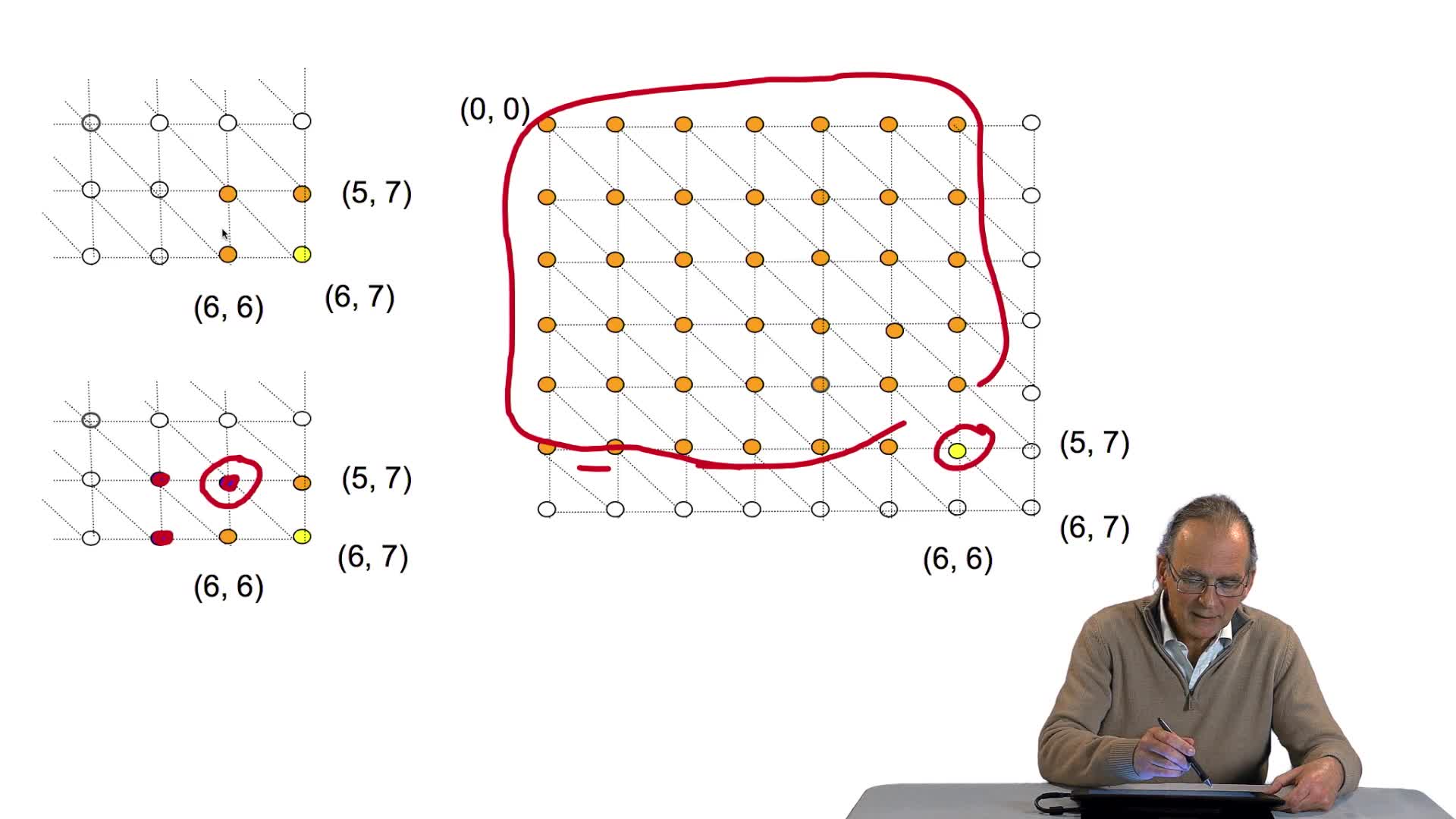
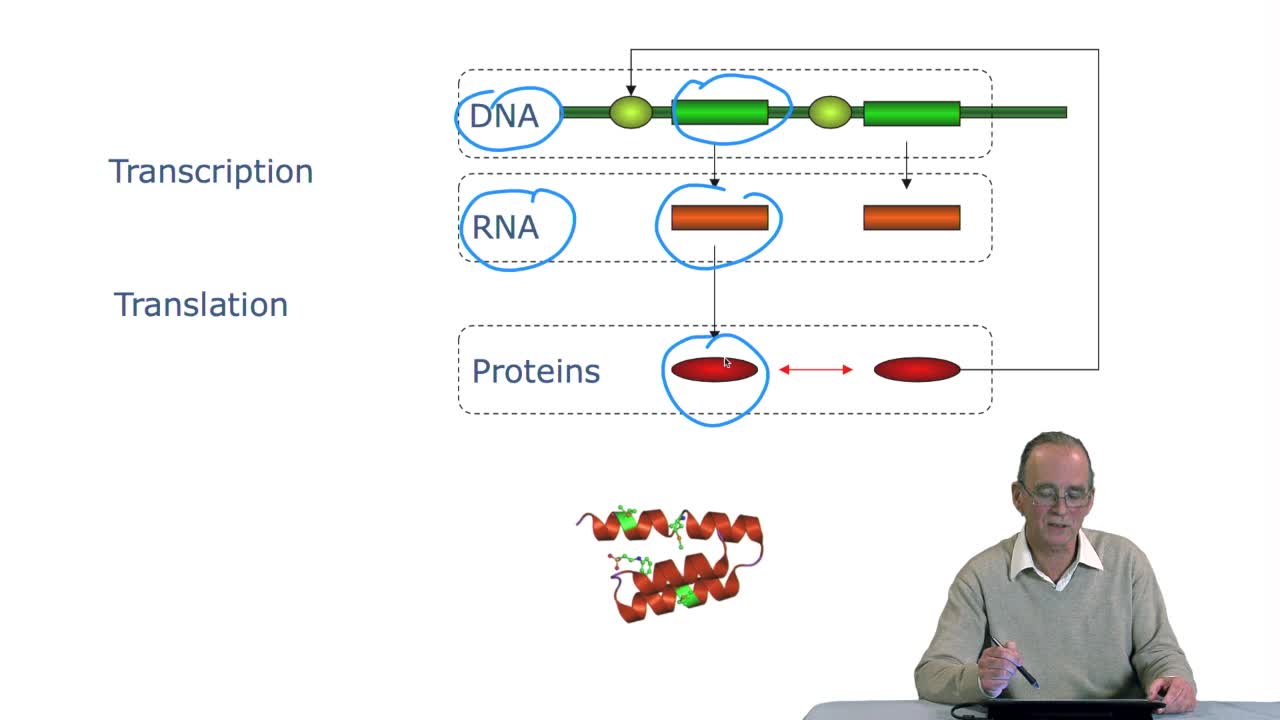
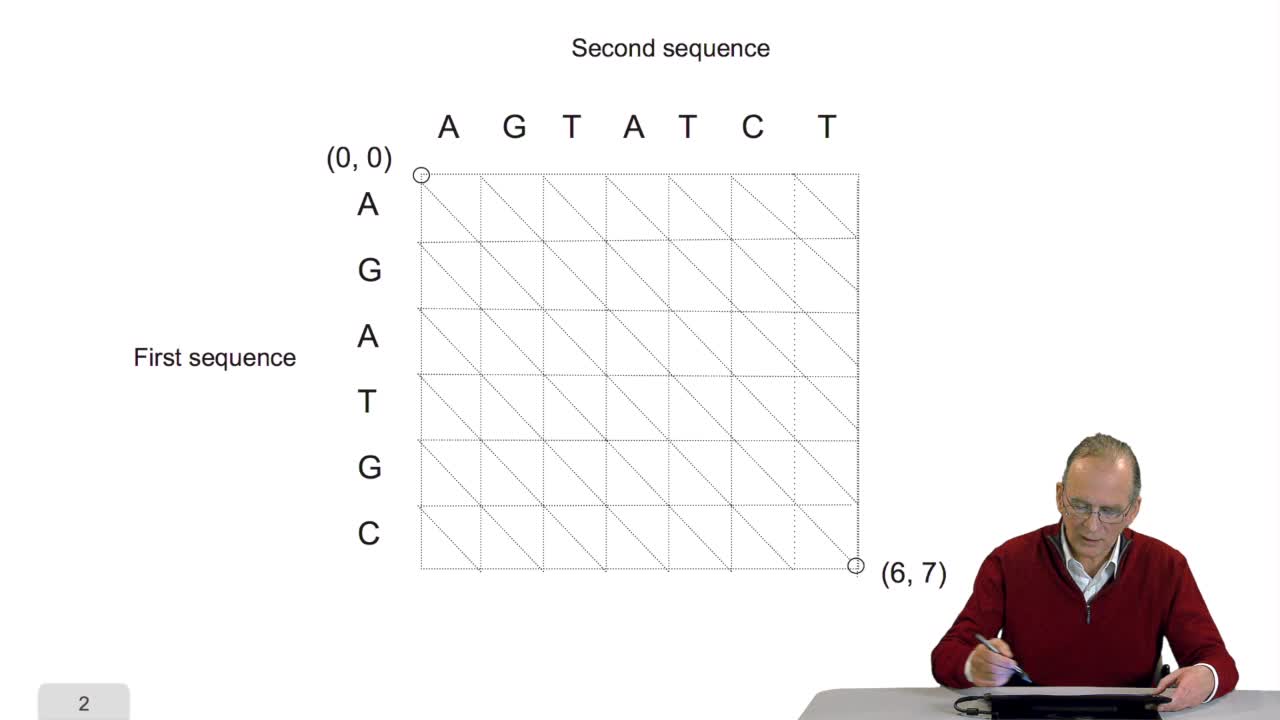
Nous cherchons à concevoir un algorithme capable de déterminer l'alignement optimal de 2 séquences. Et nous avons vu que ça revient à chercher un algorithme qui recherche un chemin optimal dans une grille. Chemin optimal, c'est-à-dire de coût de score minimal.
Pour bâtir cet algorithme, nous allons nous appuyer sur une propriété de ce chemin optimal qui est la suivante : si un chemin de longueur l est optimal, alors le chemin de longueur l-1 l'est aussi. Comment prouver cette propriété ? Très simplement en fait par l'absurde. C'est-à-dire qu'on va faire l'hypothèse contraire. C'est-à-dire que si le chemin de longueur L est optimal, il se peut que le chemin de longueur L-1, qu'il existe un chemin de longueur L-1 qui ne le soit pas. Et on arrivera à une contradiction. Ce qui va montrer par l'absurde, la véracité de cette affirmation-là. On voit également qu’un chemin de longueur L-1 correspond sur l'alignement à un alignement de longueur L-1 également. Correspondance, on l'avait vu, entre alignement et chemin...
Intervention
Dans la même collection
-
4.7. Coûts et alignement
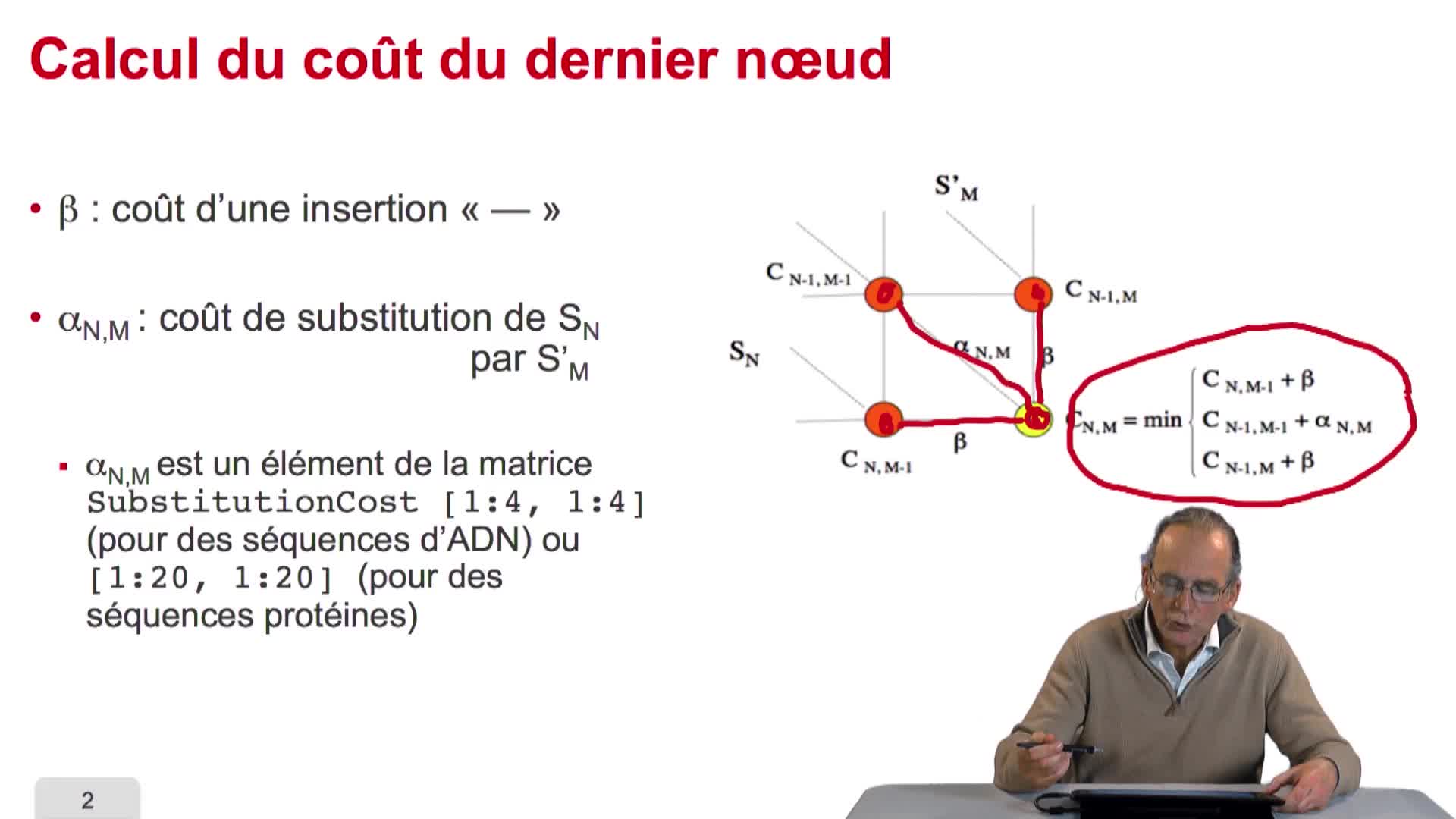
RechenmannFrançoisParmentelatThierryNous avons vu l'ébauche de notre algorithme d'alignement optimal en considérant la possibilité de calculer le coût optimal, ou score optimal, de ce dernier noeud. Et nous avons vu que le coût de ce
-
4.1. Comment prédire les fonctions des gènes/protéines ?
RechenmannFrançoisParmentelatThierryAprès avoir regardé dans les yeux, les semaines précédentes, l'ADN, vu comment cet ADN par séquençage produisait des textes, des séquences génomiques, étudié la relation entre gènes et protéines,
-
4.10. Cet algorithme est-il efficace ?
RechenmannFrançoisParmentelatThierryLa version itérative de notre algorithme d'alignement optimal de séquences est indéniablement beaucoup plus efficace que sa version récursive, puisque nous avons vu qu'il permettait d'éviter que le
-
4.4. L’alignement de séquences devient un problème d’optimisation
RechenmannFrançoisParmentelatThierryLa distance de Hamming nous donne une première possibilité de mesurer la similarité entre 2 séquences. Mais elle ne reflète pas suffisamment la réalité biologique. Qu'est-ce que j'entends par là ? On
-
4.8. Un algorithme récursif
RechenmannFrançoisParmentelatThierryNous avons désormais en main tous les éléments pour écrire notre algorithme de détermination d'un alignement optimal, ici d'un chemin optimal. Avec les notations que nous avons introduites, je vous
-
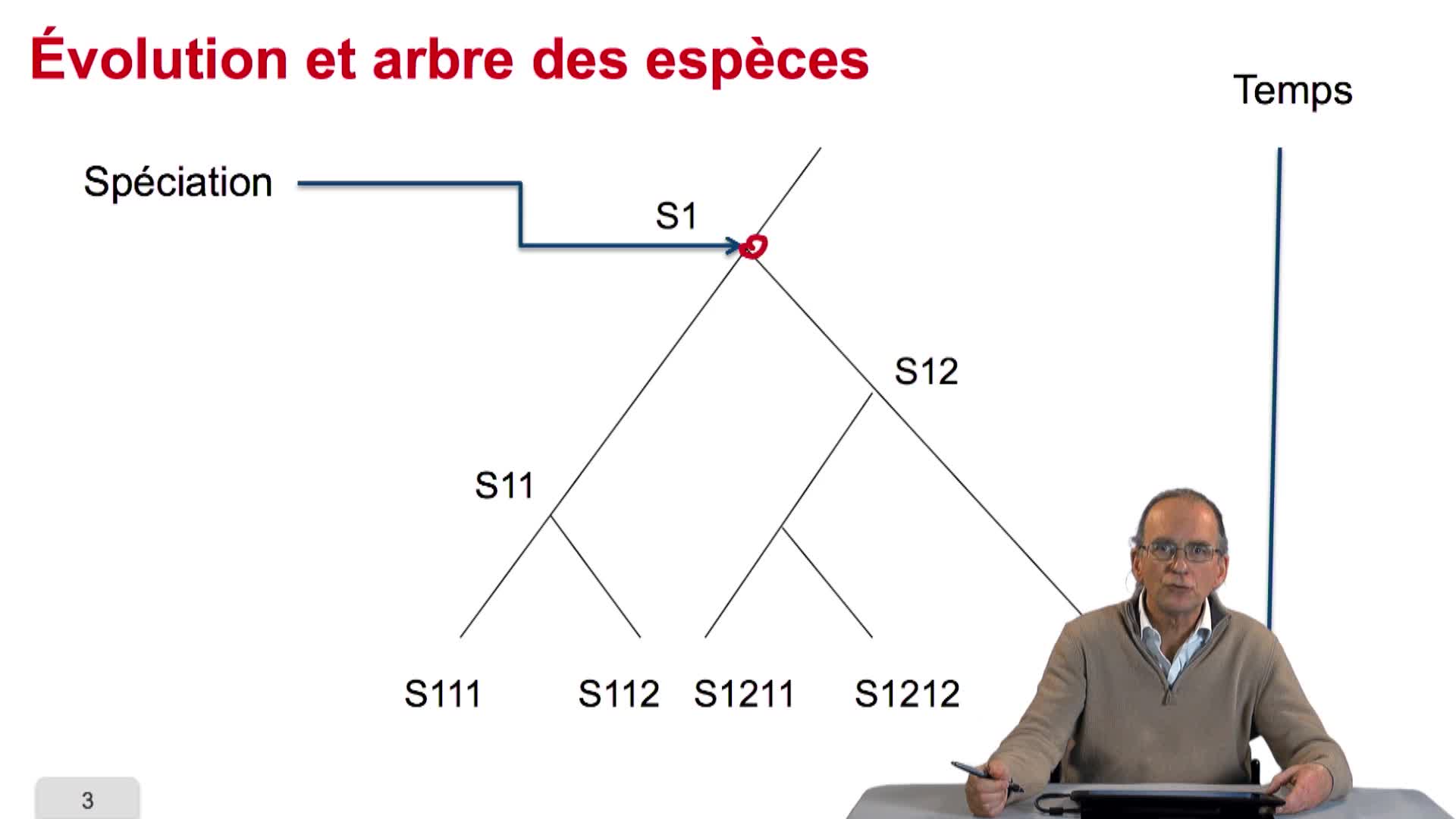
4.2. Évolution et similarité de séquences
RechenmannFrançoisParmentelatThierryAvant de chercher à quantifier ce qu'est la similarité de séquence, on peut se poser la question même de savoir pourquoi des séquences de génome sont similaires entre organismes. La réponse tient dans
-
4.5. Un alignement de séquences vu comme un chemin dans une grille
RechenmannFrançoisParmentelatThierryPour comparer deux séquences entre elles, il faut donc les aligner. Aligner ces deux séquences suppose faire des hypothèses d'insertion, délétion, aux bons endroits. Ça signifie, d'un point de vue
-
4.9. Éviter la récursivité : une version itérative
RechenmannFrançoisParmentelatThierryLa fonction récursive que nous avons obtenue est d'un code assez compact et plutôt élégant, mais effectivement peu efficace. Pourquoi ? Rappelons son fonctionnement. Cette fonction est d'abord appelée
-
4.3. Quantifier la similarité de deux séquences
RechenmannFrançoisParmentelatThierryLe principe est donc de rechercher, dans les bases de données, des séquences similaires à celles que nous sommes en train d'étudier. Nous faisons aussi l'hypothèse que plus les séquences sont
Avec les mêmes intervenants et intervenantes
-
1.8. Compressing the DNA walk
RechenmannFrançoisWe have written the algorithm for the circle DNA walk. Just a precision here: the kind of drawing we get has nothing to do with the physical drawing of the DNA molecule. It is a symbolic
-
2.7. The algorithm design trade-off
RechenmannFrançoisWe saw how to increase the efficiencyof our algorithm through the introduction of a data structure. Now let's see if we can do even better. We had a table of index and weexplain how the use of these
-
3.4. Predicting all the genes in a sequence
RechenmannFrançoisWe have written an algorithm whichis able to locate potential genes on a sequence but only on one phase because we are looking triplets after triplets. Now remember that the genes maybe located on
-
4.7. Alignment costs
RechenmannFrançoisWe have seen how we can compute the cost of the path ending on the last node of our grid if we know the cost of the sub-path ending on the three adjacent nodes. It is time now to see more deeply why
-
4.9. Recursion can be avoided: an iterative version
RechenmannFrançoisWe have written a recursive function to compute the optimal path that is an optimal alignment between two sequences. Here all the examples I gave were onDNA sequences, four letter alphabet. OK. The
-
1.3. DNA codes for genetic information
RechenmannFrançoisRemember at the heart of any cell,there is this very long molecule which is called a macromolecule for this reason, which is the DNA molecule. Now we will see that DNA molecules support what is called
-
2.1. The sequence as a model of DNA
RechenmannFrançoisWelcome back to our course on genomes and algorithms that is a computer analysis ofgenetic information. Last week we introduced the very basic concept in biology that is cell, DNA, genome, genes
-
2.9. Whole genome sequencing
RechenmannFrançoisSequencing is anexponential technology. The progresses in this technologyallow now to a sequence whole genome, complete genome. What does it mean? Well let'stake two examples: some twenty years ago,
-
3.7. Index and suffix trees
RechenmannFrançoisWe have seen with the Boyer-Moore algorithm how we can increase the efficiency of spin searching through the pre-processing of the pattern to be searched. Now we will see that an alternative way of
-
4.4. Aligning sequences is an optimization problem
RechenmannFrançoisWe have seen a nice and a quitesimple solution for measuring the similarity between two sequences. It relied on the so-called hammingdistance that is counting the number of differencesbetween two
-
5.2. The tree, an abstract object
RechenmannFrançoisWhen we speak of trees, of species,of phylogenetic trees, of course, it's a metaphoric view of a real tree. Our trees are abstract objects. Here is a tree and the different components of this tree.
-
1.6. GC and AT contents of DNA sequence
RechenmannFrançoisWe have designed our first algorithmfor counting nucleotides. Remember, what we have writtenin pseudo code is first declaration of variables. We have several integer variables that are variables which
Sur le même thème
-
Machines algorithmiques, mythes et réalités
MazenodVincentVincent Mazenod, informaticien, partage le fruit de ses réflexions sur l'évolution des outils numériques, en lien avec les problématiques de souveraineté, de sécurité et de vie privée...
-
Désassemblons le numérique - #Episode11 : Les algorithmes façonnent-ils notre société ?
SchwartzArnaudLima PillaLaércioEstériePierreSalletFrédéricFerbosAudeRoumanosRayyaChraibi KadoudIkramUn an après le tout premier hackathon sur les méthodologies d'enquêtes journalistiques sur les algorithmes, ce nouvel épisode part à la rencontre de différents points de vue sur les algorithmes.
-
Les machines à enseigner. Du livre à l'IA...
BruillardÉricQue peut-on, que doit-on déléguer à des machines ? C'est l'une des questions explorées par Éric Bruillard qui, du livre aux IA génératives, expose l'évolution des machines à enseigner...
-
Désassemblons le numérique - #Episode9 : Bientôt des supercalculateurs dans nos piscines ?
BeaumontOlivierBouzelRémiDes supercalculateurs feraient-ils bientôt leur apparition dans les piscines municipales pour les chauffer ? Réponses d'Olivier Beaumont, responsable de l'équipe-projet Topal, et Rémi Bouzel,
-
Le projet dnarXiv : Stockage de données sur des molécules d'ADN
LavenierDominiqueDuprazElsaLeblancJulienCoatrieuxGouenouDominique Lavenier, Elsa Dupraz, Julien Leblanc et Gouenou Coatrieux nous présentent le projet dnarXiv, un projet porté par le LabEx CominLabs qui explore le stockage de données sur des molécules d
-
Projection methods for community detection in complex networks
LitvakNellyCommunity detection is one of most prominent tasks in the analysis of complex networks such as social networks, biological networks, and the world wide web. A community is loosely defined as a group
-
Lara Croft. doing fieldwork under surveillance
Dall'AgnolaJasminLara Croft. Doing Fieldwork Under Surveillance Intervention de Jasmin Dall'Agnola (The George Washington University), dans le cadre du Colloque coorganisé par Anders Albrechtslund, professeur en
-
Containing predictive tokens in the EU
CzarnockiJanContaining Predictive Tokens in the EU – Mapping the Laws Against Digital Surveillance, intervention de Jan Czarnocki (KU Leuven), dans le cadre du Colloque coorganisé par Anders Albrechtslund,
-
Ivan Murit - Processus de création d'images
MuritIvanJe vais présenter une manière décalée d'aborder les outils d'impression. Pour cela nous ne partirons pas de l'envie d'imprimer une image préexistante, mais d'avant cela : comment se crée une forme
-
Le Creativ’Lab, au cœur de la robotique et de l’intelligence artificielle (ASR N°18 - LORIA)
HénaffPatrickLefebvreSylvainLe LORIA, laboratoire phare de la Grande Région dans le domaine de l’informatique, propose de rendre la recherche plus ouverte, plus collaborative, plus ambitieuse… en un mot, plus créative, à travers
-
Les algorithmes de Parcoursup
MathieuClaireL’objectif de la journée « Algorithmes d’aide à la décision publique » était de sensibiliser le grand public aux rôles des algorithmes d’aide à la décision publique utilisés par exemple pour l
-
Algorithmes d'aide à la décision publique / Ouverture
RéveillèreLaurentMaveyraud-TricoireSamuelBlancXavierBertrandYvesMainguenéMarcL’objectif de la journée « Algorithmes d’aide à la décision publique » était de sensibiliser le grand public aux rôles des algorithmes d’aide à la décision publique utilisés par exemple pour l
