4. Sequences comparison

Descriptif
Table of contents
4.1. How to predict gene/protein functions?
4.2. Why gene/protein sequences may be similar?
4.3. Measuring sequence similarity
4.4. Aligning sequences is an optimization problem
4.5. A sequence alignment as a path
4.6. A path is optimal if all its sub-paths are optimal
4.7. Alignment costs
4.8. A recursive algorithm
4.9. Recursion can be avoided: an iterative version
4.10. How efficient is this algorithm?
Vidéos
4.1. How to predict gene/protein functions?
Last week we have seen that annotating a genome means first locating the genes on the DNA sequences that is the genes, the region coding for proteins. But this is indeed the first step,the next very
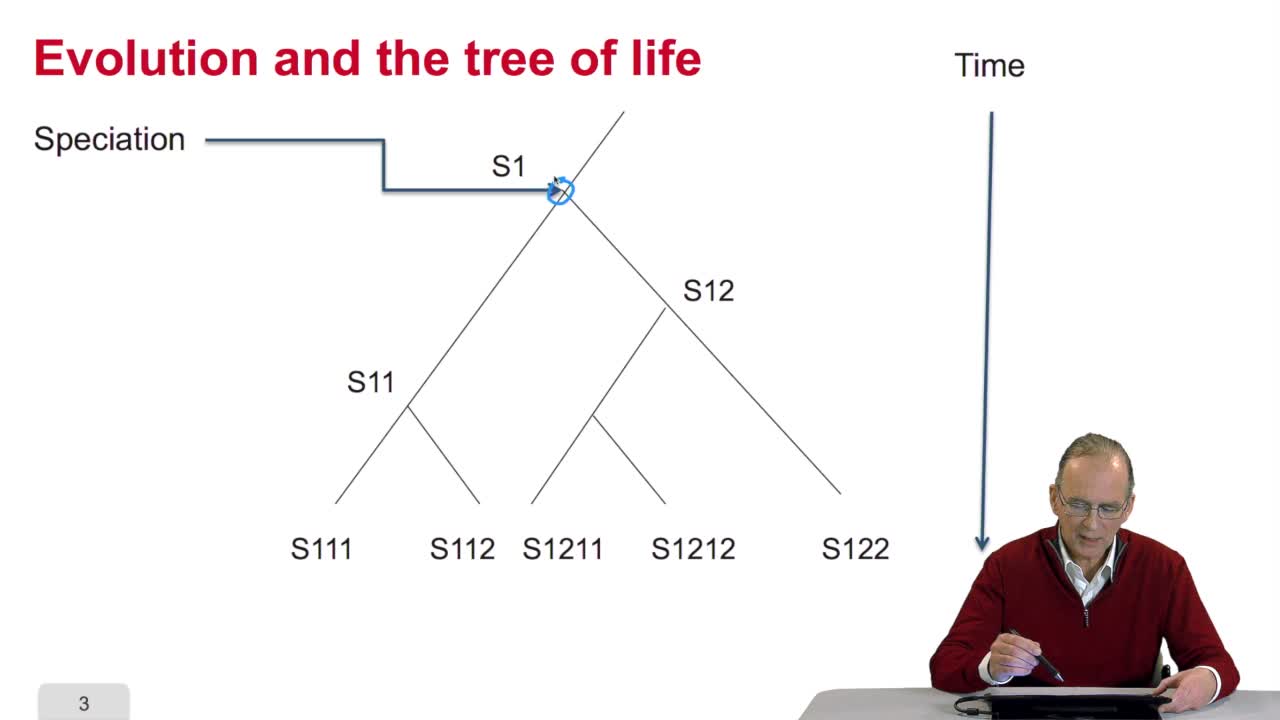
4.2. Why gene/protein sequences may be similar?
Before measuring the similaritybetween the sequences, it's interesting to answer the question: why gene or protein sequences may be similar? It is indeed veryinteresting because the answer is related
4.3. Measuring sequence similarity
So we understand why gene orprotein sequences may be similar. It's because they evolve togetherwith the species and they evolve in time, there aremodifications in the sequence and that the sequence
4.4. Aligning sequences is an optimization problem
We have seen a nice and a quitesimple solution for measuring the similarity between two sequences. It relied on the so-called hammingdistance that is counting the number of differencesbetween two
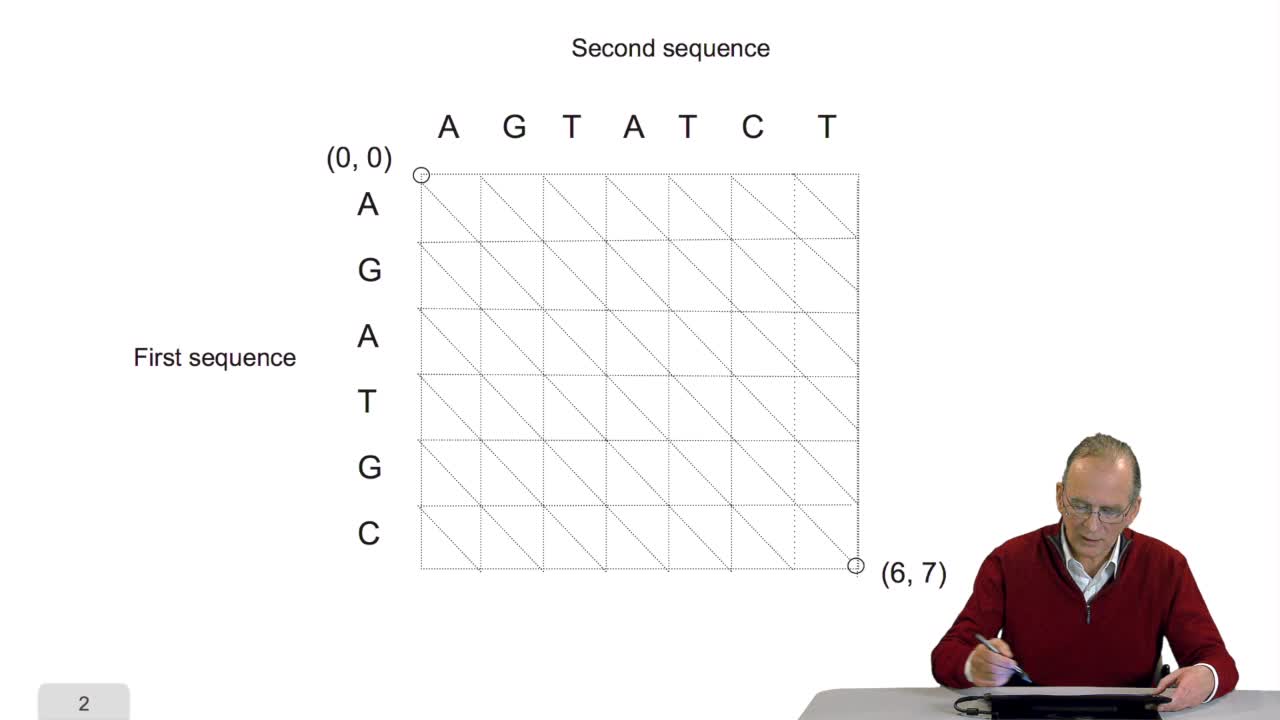
4.5. A sequence alignment as a path
Comparing two sequences and thenmeasuring their similarities is an optimization problem. Why? Because we have seen thatwe have to take into account substitution and deletion. During the alignment, the
4.6. A path is optimal if all its sub-paths are optimal
A sequence alignment between two sequences is a path in a grid. So that, an optimal sequence alignmentis an optimal path in the same grid. We'll see now that a property of this optimal path provides
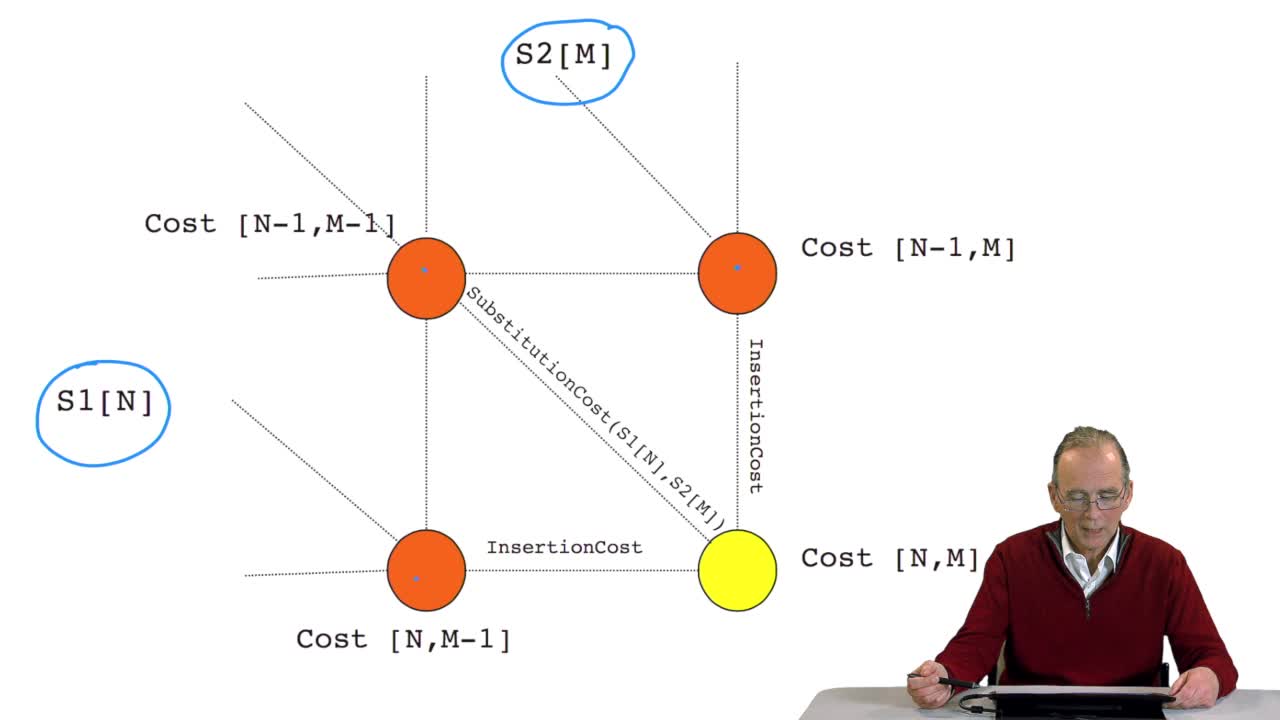
4.7. Alignment costs
We have seen how we can compute the cost of the path ending on the last node of our grid if we know the cost of the sub-path ending on the three adjacent nodes. It is time now to see more deeply why
4.8. A recursive algorithm
We have seen how we can computethe optimal cost, the ending node of our grid if we know the optimal cost of the three adjacent nodes. This is this computation scheme we can see here using the notation
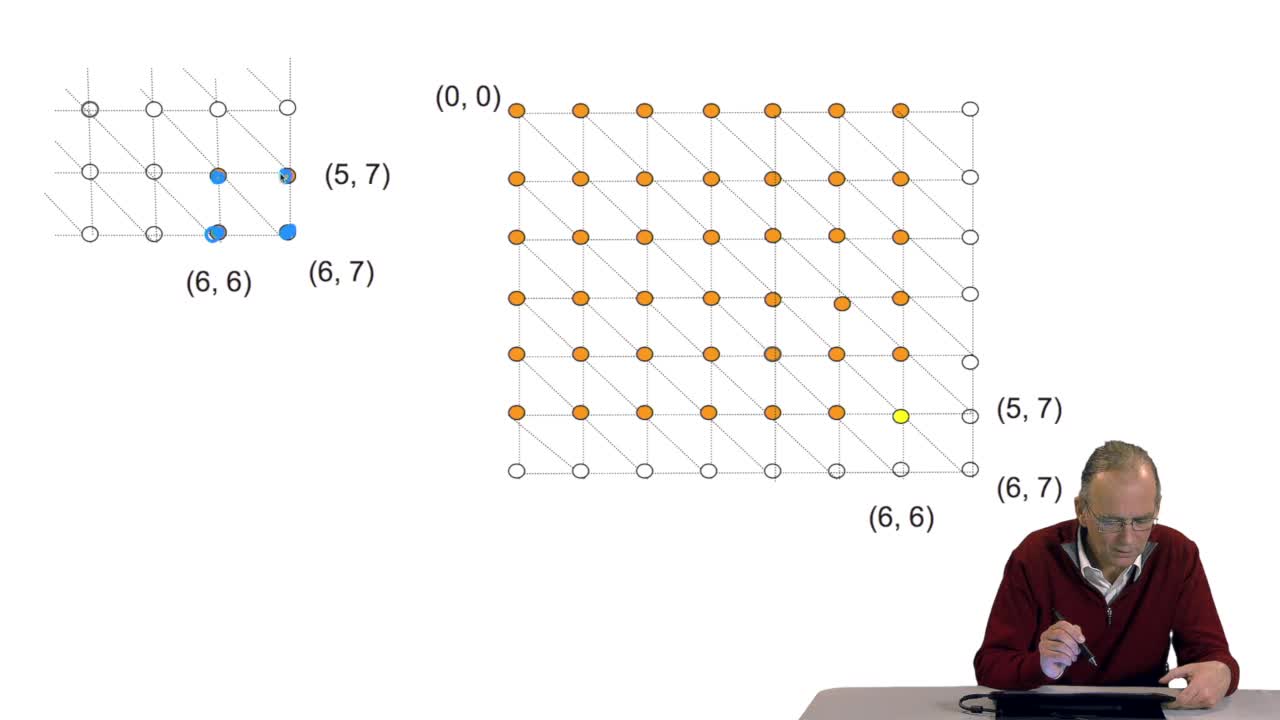
4.9. Recursion can be avoided: an iterative version
We have written a recursive function to compute the optimal path that is an optimal alignment between two sequences. Here all the examples I gave were onDNA sequences, four letter alphabet. OK. The
4.10. How efficient is this algorithm?
We have seen the principle of an iterative algorithm in two paths for aligning and comparing two sequences of characters, here DNA sequences. And we understoodwhy the iterative version is much more
Intervenants et intervenantes
Ingénieur. Auteur d'une thèse de docteur-ingénieur en sciences appliquées (Grenoble INPG, 1976). - HDR. Directeur de thèse à Grenoble INPG (1990-1994-) et à l'université de Grenoble 1. Directeur de recherche au centre Inria Grenoble – Rhône-Alpes (2002, 2015)