Notice
4.10. How efficient is this algorithm?
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
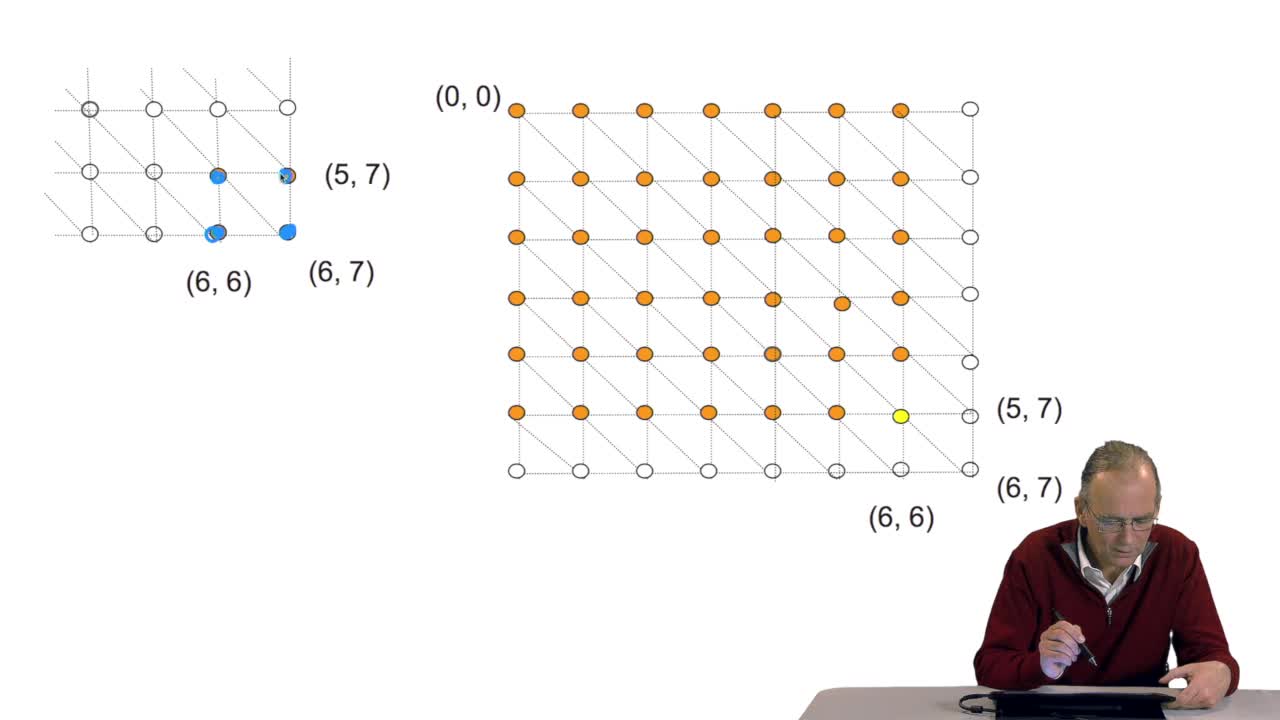
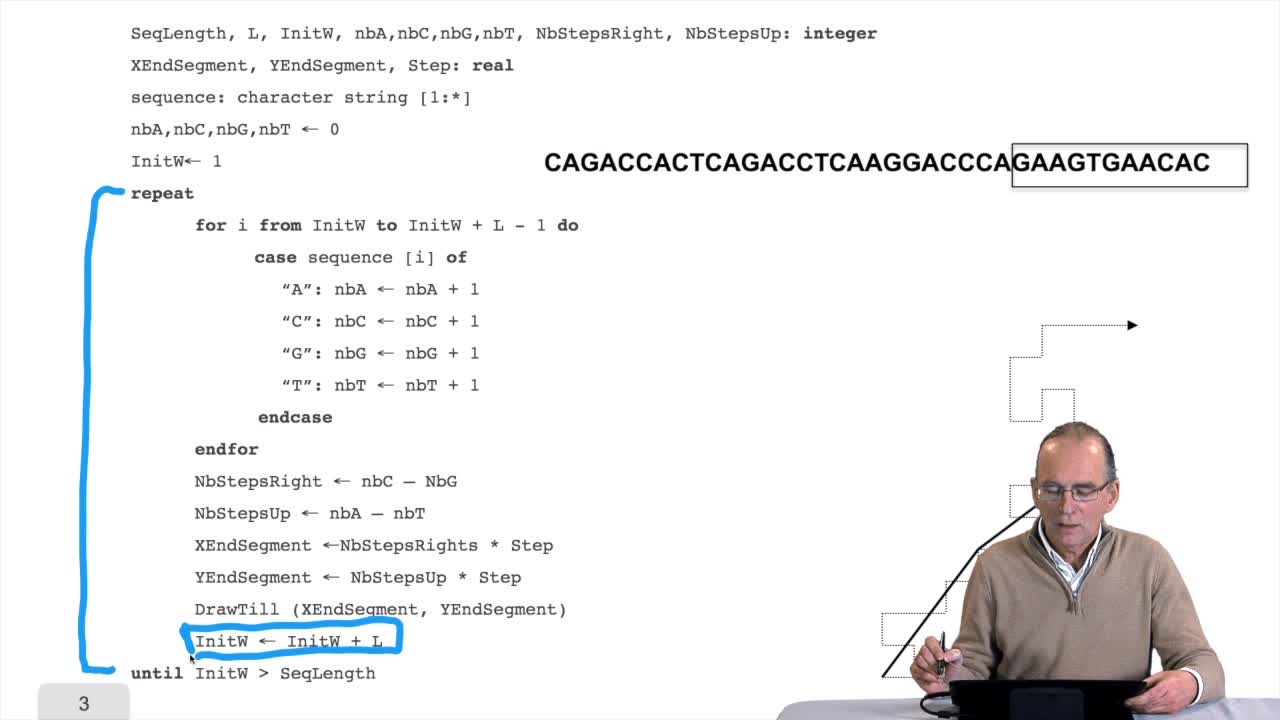
We have seen the principle of an iterative algorithm in two paths for aligning and comparing two sequences of characters, here DNA sequences. And we understoodwhy the iterative version is much more efficient than the recursive version. But, how efficient is reallythis iterative algorithm? You remember that in order to measure the efficiency of algorithms, the computer scientists do not use any mean of measuring the time or any other thing. They evaluate the number of timethe main operation inside the algorithm is executed. In the caseof this Needleman and Wunsch algorithm which has been published 40 years ago, the operation which is critical is the comparisonbetween two letters of a pair of letters. It's easy, if you look at the algorithm, to find that the number of comparison is of the order of N multiplied by M with N and M being the lengths of the sequences. We say that the algorithmic complexity of this algorithm is quadratic. What does it mean? It means thatif the lengths of the sequences double, the execution time will be multiplied by four. It's easy to see. First, you have two sequences of lengths N and M. You double the length of the first sequence and you double the length of the fourth sequence since the number of comparison is the result of the multiplication of these two values, you see that of course you multiply the execution time by four.
Intervention / Responsable scientifique
Thème
Documentation
Dans la même collection
-
4.6. A path is optimal if all its sub-paths are optimal
RechenmannFrançoisA sequence alignment between two sequences is a path in a grid. So that, an optimal sequence alignmentis an optimal path in the same grid. We'll see now that a property of this optimal path provides
-
4.1. How to predict gene/protein functions?
RechenmannFrançoisLast week we have seen that annotating a genome means first locating the genes on the DNA sequences that is the genes, the region coding for proteins. But this is indeed the first step,the next very
-
4.9. Recursion can be avoided: an iterative version
RechenmannFrançoisWe have written a recursive function to compute the optimal path that is an optimal alignment between two sequences. Here all the examples I gave were onDNA sequences, four letter alphabet. OK. The
-
4.4. Aligning sequences is an optimization problem
RechenmannFrançoisWe have seen a nice and a quitesimple solution for measuring the similarity between two sequences. It relied on the so-called hammingdistance that is counting the number of differencesbetween two
-
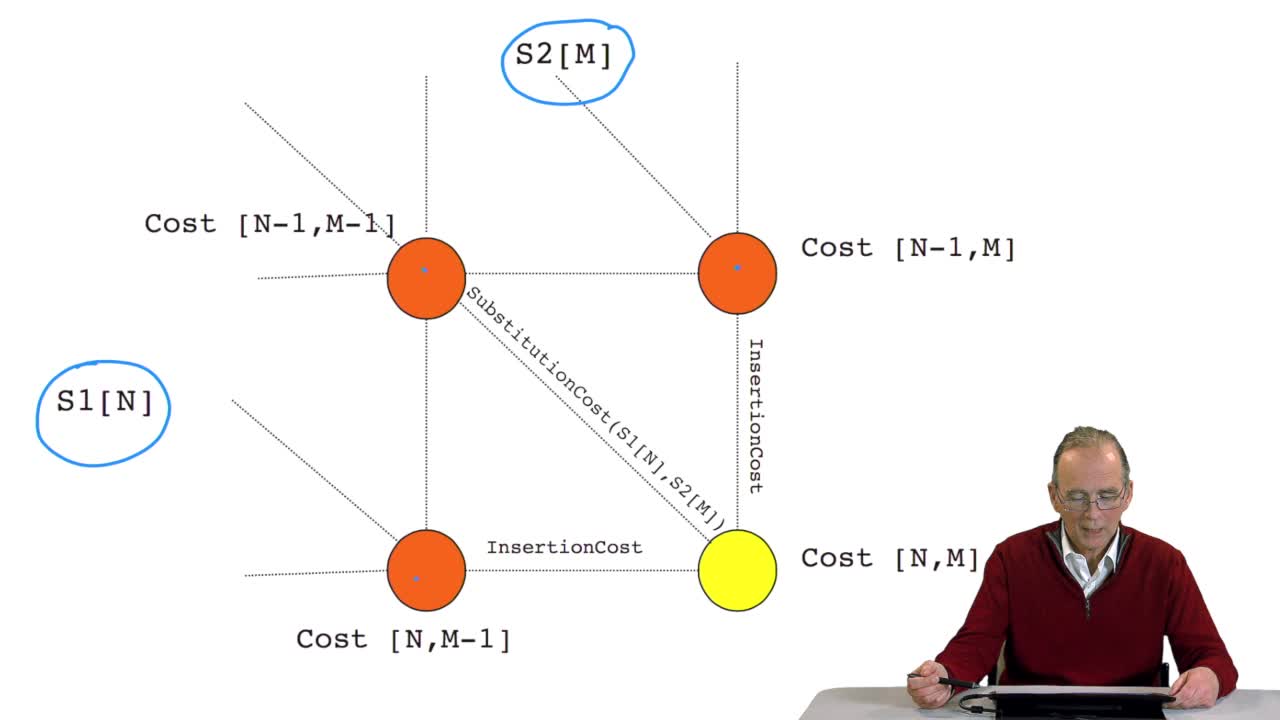
4.7. Alignment costs
RechenmannFrançoisWe have seen how we can compute the cost of the path ending on the last node of our grid if we know the cost of the sub-path ending on the three adjacent nodes. It is time now to see more deeply why
-
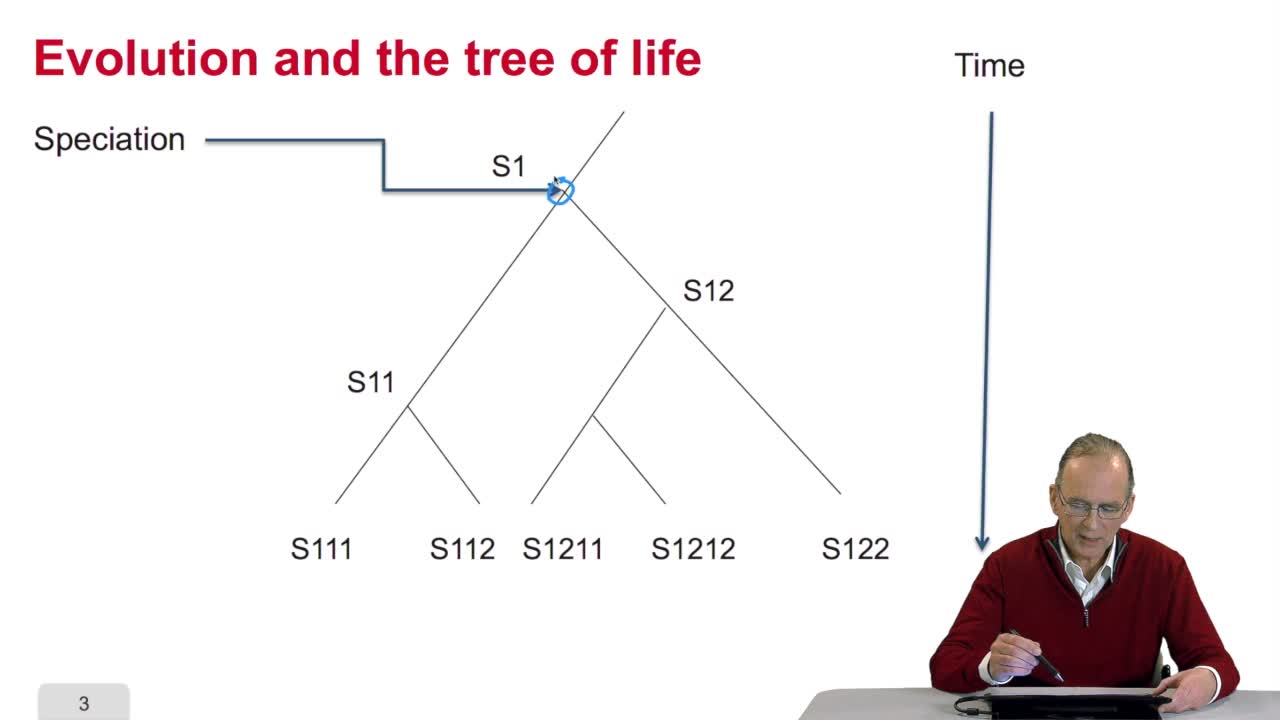
4.2. Why gene/protein sequences may be similar?
RechenmannFrançoisBefore measuring the similaritybetween the sequences, it's interesting to answer the question: why gene or protein sequences may be similar? It is indeed veryinteresting because the answer is related
-
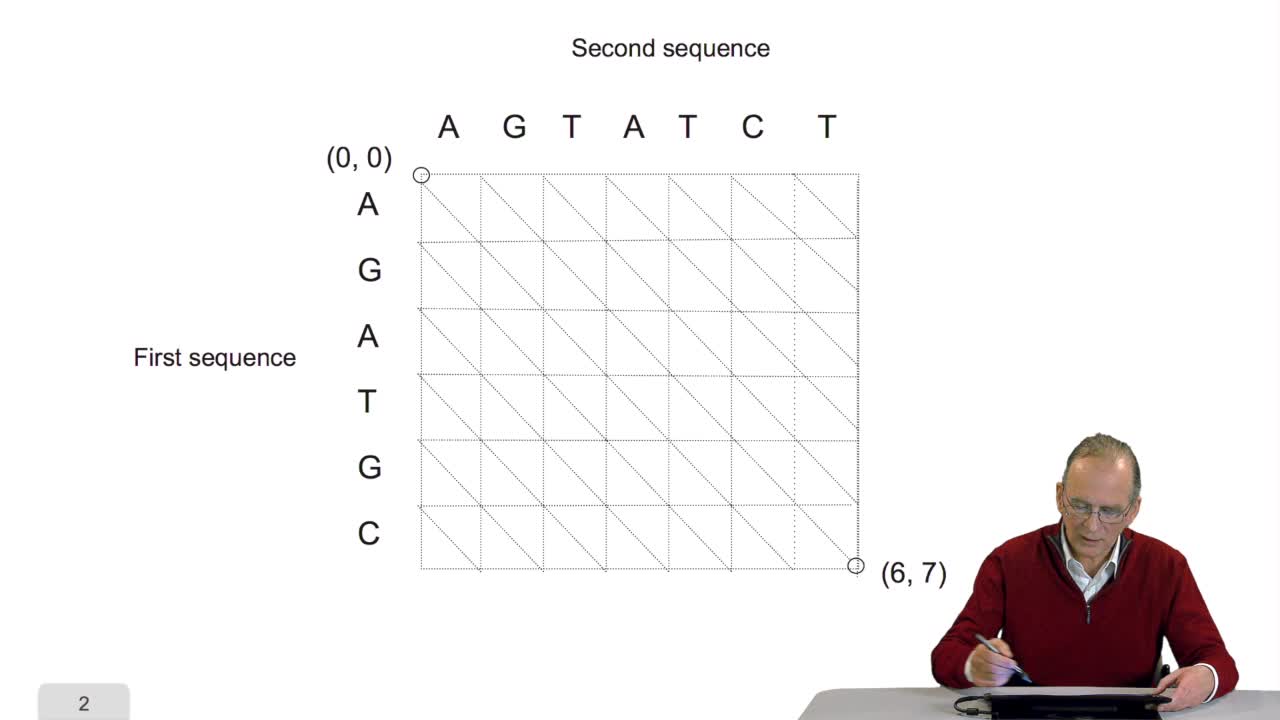
4.5. A sequence alignment as a path
RechenmannFrançoisComparing two sequences and thenmeasuring their similarities is an optimization problem. Why? Because we have seen thatwe have to take into account substitution and deletion. During the alignment, the
-
4.8. A recursive algorithm
RechenmannFrançoisWe have seen how we can computethe optimal cost, the ending node of our grid if we know the optimal cost of the three adjacent nodes. This is this computation scheme we can see here using the notation
-
4.3. Measuring sequence similarity
RechenmannFrançoisSo we understand why gene orprotein sequences may be similar. It's because they evolve togetherwith the species and they evolve in time, there aremodifications in the sequence and that the sequence
Avec les mêmes intervenants et intervenantes
-
1.6. GC and AT contents of DNA sequence
RechenmannFrançoisWe have designed our first algorithmfor counting nucleotides. Remember, what we have writtenin pseudo code is first declaration of variables. We have several integer variables that are variables which
-
2.5. Implementing the genetic code
RechenmannFrançoisRemember we were designing our translation algorithm and since we are a bit lazy, we decided to make the hypothesis that there was the adequate function forimplementing the genetic code. It's now time
-
3.2. A simple algorithm for gene prediction
RechenmannFrançoisBased on the principle we statedin the last session, we will now write in pseudo code a firstalgorithm for locating genes on a bacterial genome. Remember first how this algorithm should work, we first
-
3.10. Gene prediction in eukaryotic genomes
RechenmannFrançoisIf it is possible to have verygood predictions for bacterial genes, it's certainly not the caseyet for eukaryotic genomes. Eukaryotic cells have manydifferences in comparison to prokaryotic cells. You
-
4.8. A recursive algorithm
RechenmannFrançoisWe have seen how we can computethe optimal cost, the ending node of our grid if we know the optimal cost of the three adjacent nodes. This is this computation scheme we can see here using the notation
-
5.7. The application domains in microbiology
RechenmannFrançoisBioinformatics relies on many domains of mathematics and computer science. Of course, algorithms themselves on character strings are important in bioinformatics, we have seen them. Algorithms and
-
1.1. The cell, atom of the living world
RechenmannFrançoisWelcome to this introduction to bioinformatics. We will speak of genomes and algorithms. More specifically, we will see how genetic information can be analysed by algorithms. In these five weeks to
-
1.9. Predicting the origin of DNA replication?
RechenmannFrançoisWe have seen a nice algorithm to draw, let's say, a DNA sequence. We will see that first, we have to correct a little bit this algorithm. And then we will see how such as imple algorithm can provide
-
2.8. DNA sequencing
RechenmannFrançoisDuring the last session, I explained several times how it was important to increase the efficiency of sequences processing algorithm because sequences arevery long and there are large volumes of
-
3.5. Making the predictions more reliable
RechenmannFrançoisWe have got a bacterial gene predictor but the way this predictor works is rather crude and if we want to have more reliable results, we have to inject into this algorithmmore biological knowledge. We
-
4.6. A path is optimal if all its sub-paths are optimal
RechenmannFrançoisA sequence alignment between two sequences is a path in a grid. So that, an optimal sequence alignmentis an optimal path in the same grid. We'll see now that a property of this optimal path provides
-
5.5. Differences are not always what they look like
RechenmannFrançoisThe algorithm we have presented works on an array of distance between sequences. These distances are evaluated on the basis of differences between the sequences. The problem is that behind the
