Notice
4.7. Alignment costs
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
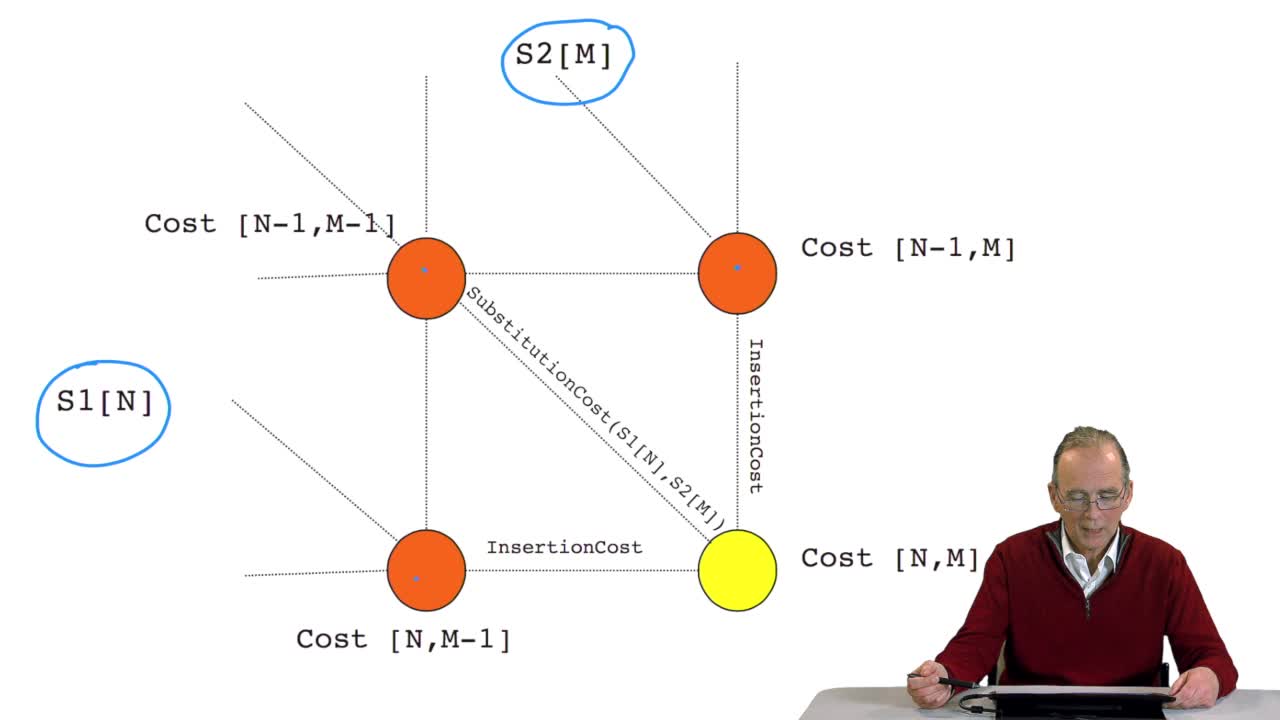
We have seen how we can compute the cost of the path ending on the last node of our grid if we know the cost of the sub-path ending on the three adjacent nodes. It is time now to see more deeply why these costs are used to compute the cost in the last node. So again, we saw how we can compute the cost here of the path ending on that node if we know the cost of the sub-path ending on these three red nodes. Indeed, if we come from that node, the cost on that node will be the cost of that node plus the cost of the gap that is an insertion cost. If we come from that node, the situation is similar, the cost of that node will be the cost of thatone plus the same insertion cost. If we come from that node, thecost here will be the sum of the cost of that node plus the code of the substitution of the letter N of the sequence by letter M of the second sequence. And this cost is known withinthe substitution matrix, here, which tells for each pair of characters, here in the four letter alphabet, the cost of substituting oneletter, one nucleotide by another one. So, now since we want to havehere the minimal cost what we do is we take, we return as the value of the cost here the minimum of these three expressions.
Intervention / Responsable scientifique
Thème
Documentation
Dans la même collection
-
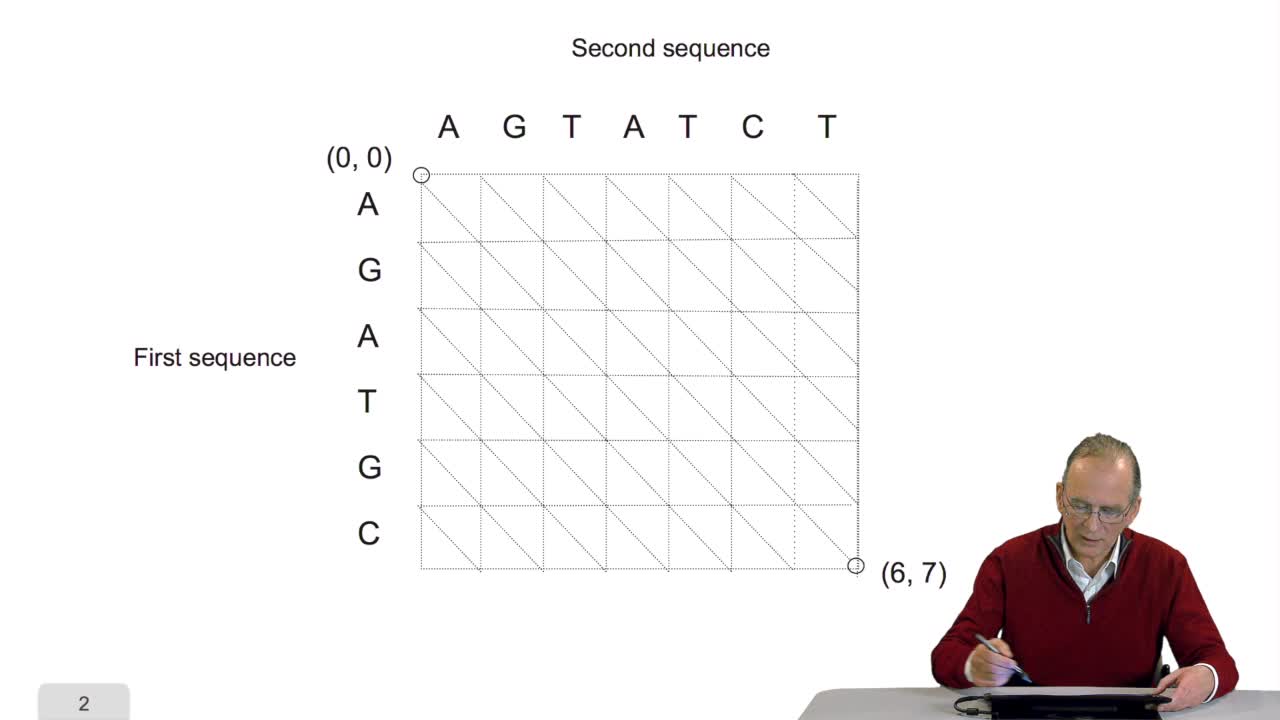
4.5. A sequence alignment as a path
RechenmannFrançoisComparing two sequences and thenmeasuring their similarities is an optimization problem. Why? Because we have seen thatwe have to take into account substitution and deletion. During the alignment, the
-
4.9. Recursion can be avoided: an iterative version
RechenmannFrançoisWe have written a recursive function to compute the optimal path that is an optimal alignment between two sequences. Here all the examples I gave were onDNA sequences, four letter alphabet. OK. The
-
4.3. Measuring sequence similarity
RechenmannFrançoisSo we understand why gene orprotein sequences may be similar. It's because they evolve togetherwith the species and they evolve in time, there aremodifications in the sequence and that the sequence
-
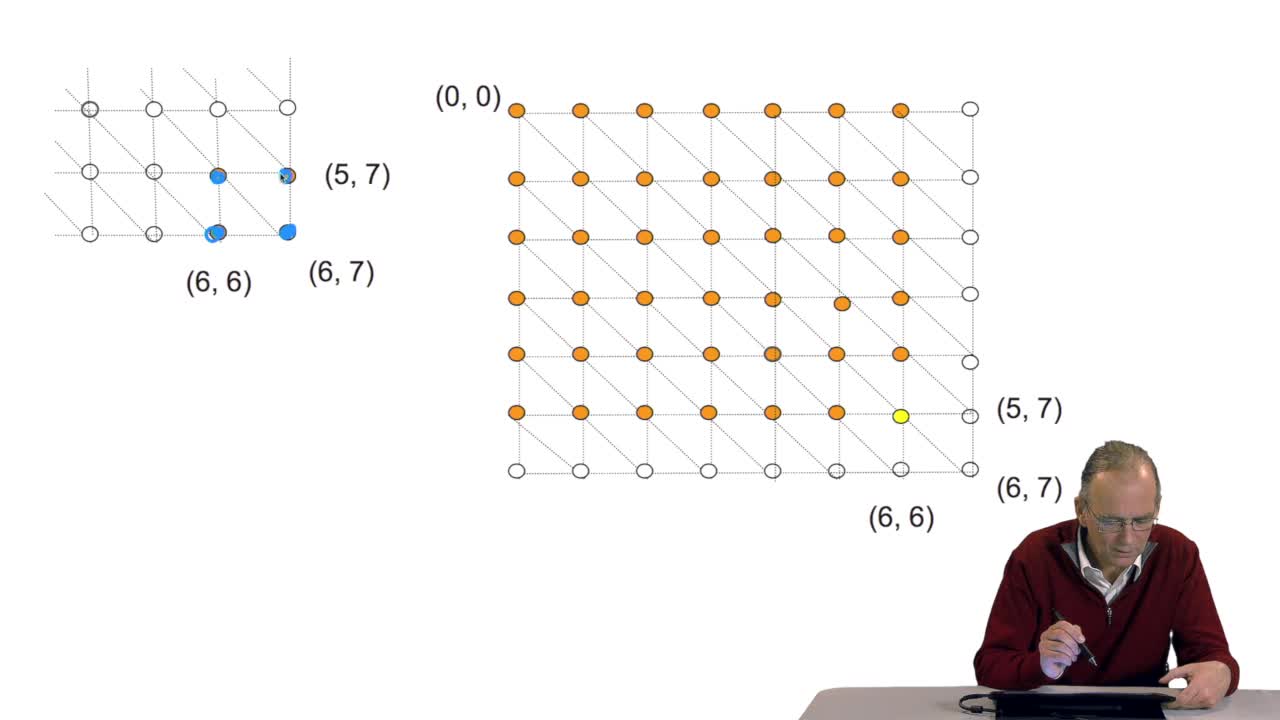
4.6. A path is optimal if all its sub-paths are optimal
RechenmannFrançoisA sequence alignment between two sequences is a path in a grid. So that, an optimal sequence alignmentis an optimal path in the same grid. We'll see now that a property of this optimal path provides
-
4.1. How to predict gene/protein functions?
RechenmannFrançoisLast week we have seen that annotating a genome means first locating the genes on the DNA sequences that is the genes, the region coding for proteins. But this is indeed the first step,the next very
-
4.10. How efficient is this algorithm?
RechenmannFrançoisWe have seen the principle of an iterative algorithm in two paths for aligning and comparing two sequences of characters, here DNA sequences. And we understoodwhy the iterative version is much more
-
4.4. Aligning sequences is an optimization problem
RechenmannFrançoisWe have seen a nice and a quitesimple solution for measuring the similarity between two sequences. It relied on the so-called hammingdistance that is counting the number of differencesbetween two
-
4.8. A recursive algorithm
RechenmannFrançoisWe have seen how we can computethe optimal cost, the ending node of our grid if we know the optimal cost of the three adjacent nodes. This is this computation scheme we can see here using the notation
-
4.2. Why gene/protein sequences may be similar?
RechenmannFrançoisBefore measuring the similaritybetween the sequences, it's interesting to answer the question: why gene or protein sequences may be similar? It is indeed veryinteresting because the answer is related
Avec les mêmes intervenants et intervenantes
-
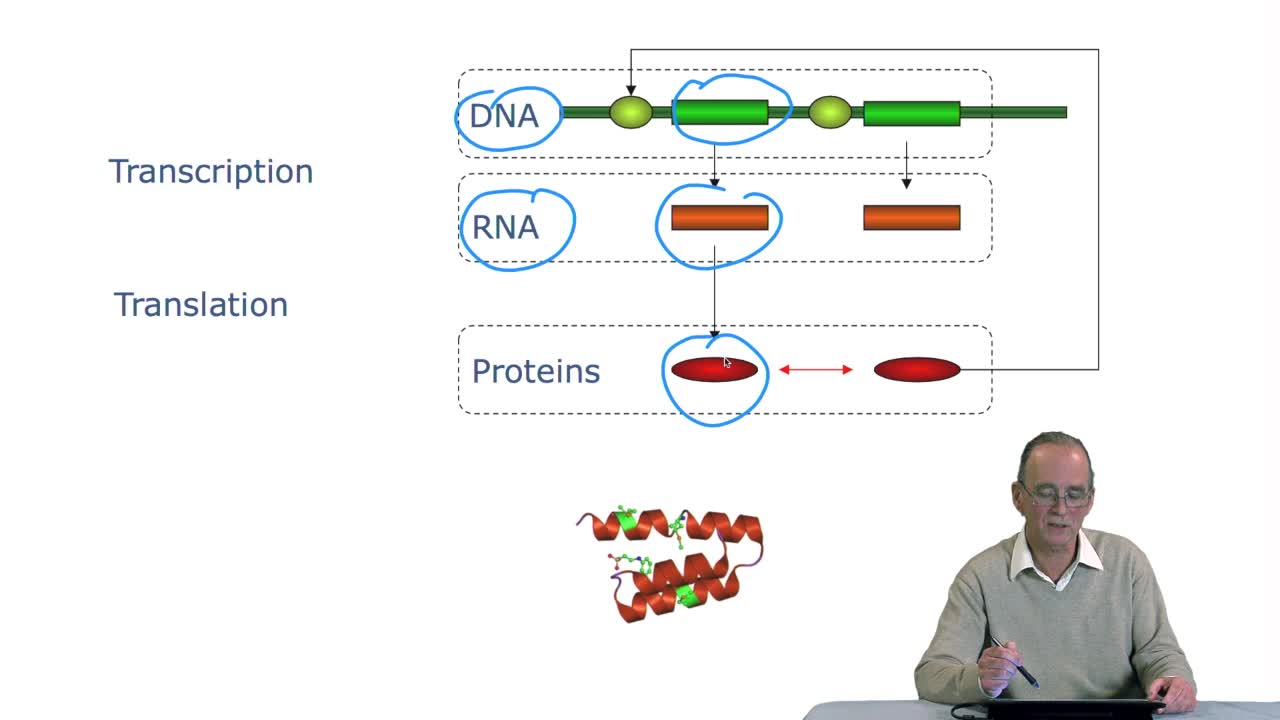
1.2. At the heart of the cell: the DNA macromolecule
RechenmannFrançoisDuring the last session, we saw how at the heart of the cell there's DNA in the nucleus, sometimes of cells, or directly in the cytoplasm of the bacteria. The DNA is what we call a macromolecule, that
-
1.10. Overlapping sliding window
RechenmannFrançoisWe have made some drawings along a genomic sequence. And we have seen that although the algorithm is quite simple, even if some points of the algorithmare bit trickier than the others, we were able to
-
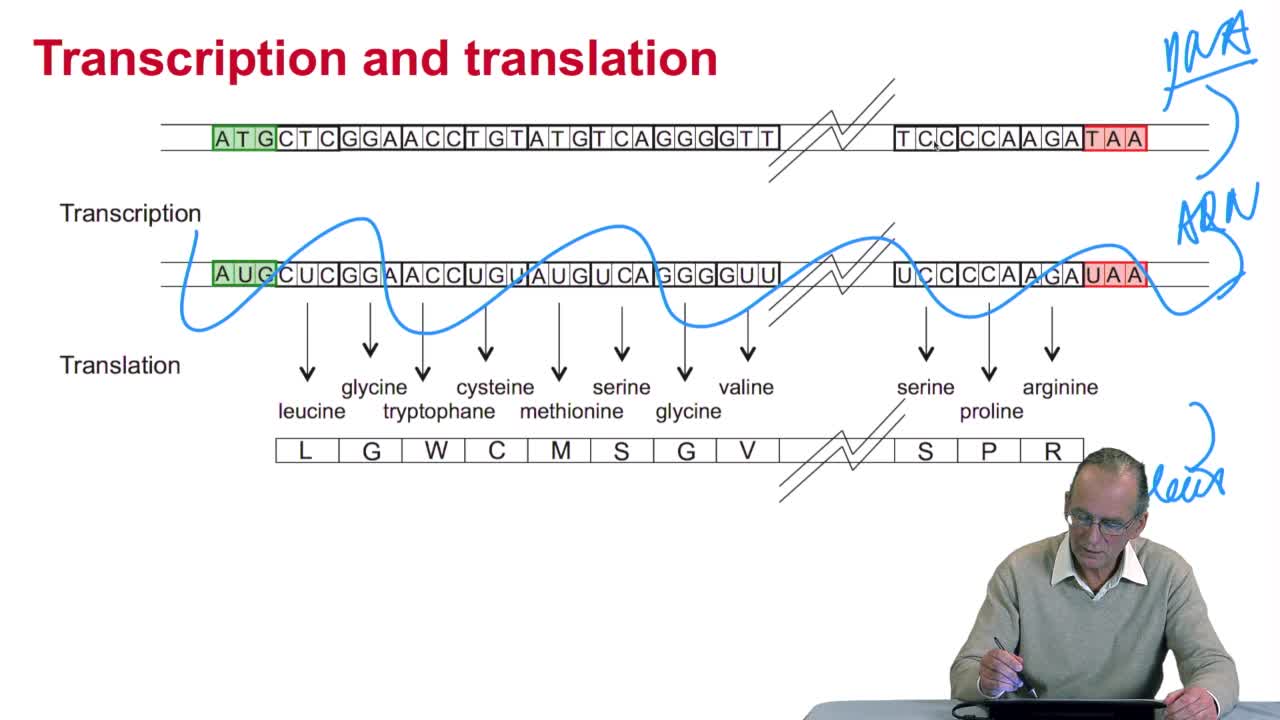
2.3. The genetic code
RechenmannFrançoisGenes code for proteins. What is the correspondence betweenthe genes, DNA sequences, and the structure of proteins? The correspondence isthe genetic code. Proteins have indeedsequences of amino acids.
-
3.6. Boyer-Moore algorithm
RechenmannFrançoisWe have seen how we can make gene predictions more reliable through searching for all the patterns,all the occurrences of patterns. We have seen, for example, howif we locate the RBS, Ribosome
-
4.4. Aligning sequences is an optimization problem
RechenmannFrançoisWe have seen a nice and a quitesimple solution for measuring the similarity between two sequences. It relied on the so-called hammingdistance that is counting the number of differencesbetween two
-
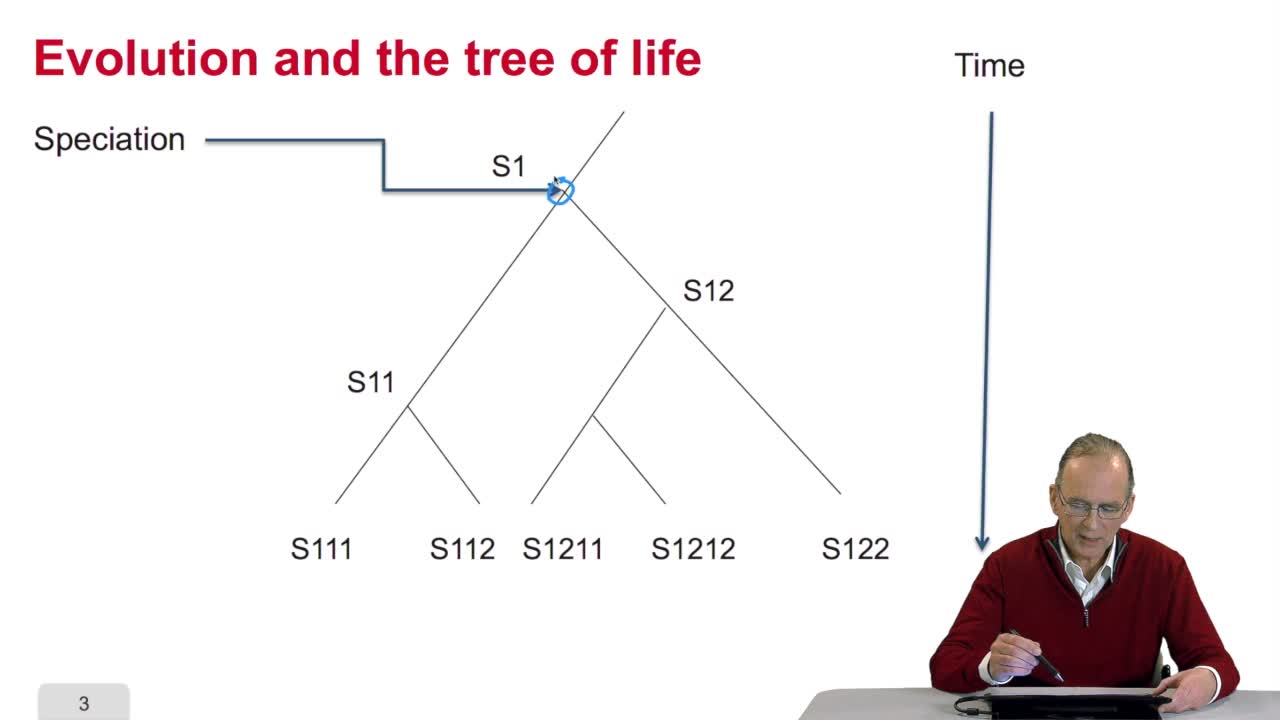
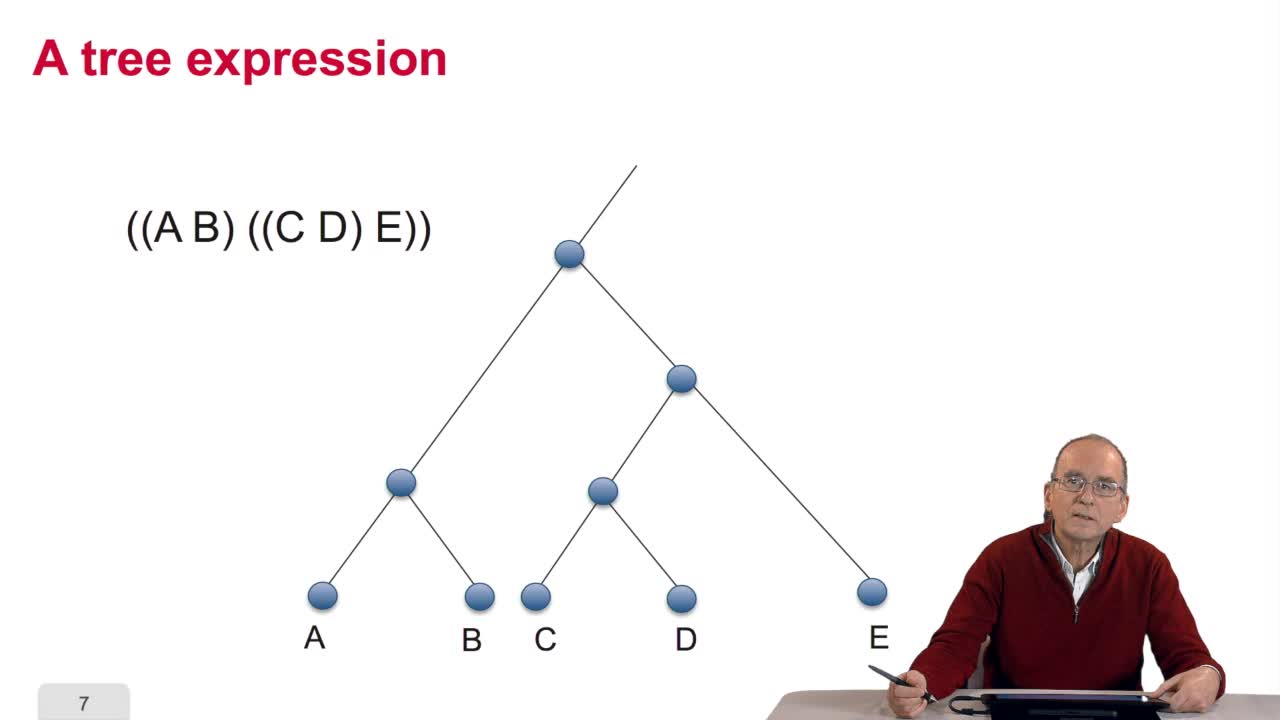
5.2. The tree, an abstract object
RechenmannFrançoisWhen we speak of trees, of species,of phylogenetic trees, of course, it's a metaphoric view of a real tree. Our trees are abstract objects. Here is a tree and the different components of this tree.
-
1.5. Counting nucleotides
RechenmannFrançoisIn this session, don't panic. We will design our first algorithm. This algorithm is forcounting nucleotides. The idea here is that as an input,you have a sequence of nucleotides, of bases, of letters,
-
2.4. A translation algorithm
RechenmannFrançoisWe have seen that the genetic codeis a correspondence between the DNA or RNA sequences and aminoacid sequences that is proteins. Our aim here is to design atranslation algorithm, we make the
-
3.1. All genes end on a stop codon
RechenmannFrançoisLast week we studied genes and proteins and so how genes, portions of DNA, are translated into proteins. We also saw the very fast evolutionof the sequencing technology which allows for producing
-
3.9. Benchmarking the prediction methods
RechenmannFrançoisIt is necessary to underline that gene predictors produce predictions. Predictions mean that you have no guarantees that the coding sequences, the coding regions,the genes you get when applying your
-
4.8. A recursive algorithm
RechenmannFrançoisWe have seen how we can computethe optimal cost, the ending node of our grid if we know the optimal cost of the three adjacent nodes. This is this computation scheme we can see here using the notation
-
5.6. The diversity of bioinformatics algorithms
RechenmannFrançoisIn this course, we have seen a very little set of bioinformatic algorithms. There exist numerous various algorithms in bioinformatics which deal with a large span of classes of problems. For example,