Notice
5.5. Differences are not always what they look like
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
The algorithm we have presented works on an array of distance between sequences. These distances are evaluated on the basis of differences between the sequences. The problem is that behind the differences we observed on the set of sequences, there may beother mutations which cannot be observed and we should modify the distances. We will have a look at some simple cases of these observed differences which may correspond to hidden differences and then we will see how the evaluation, computationof the number of differences may be affected. The simple case is this one, aunique substitution between, in the sequence One we have a Cand it turns out that in the sequence Two, there is a mutation, C becomes A. So what we observed is one mutation and the actual substitution is also one. Let's look, here we have two sequencesand here we have a mutation. OK. One difference, one mutation so in that case it's correct. A first case in which there is a discrepancy between the substitutions, number of substitutions beingobserved and the number of actual substitutions is in the case of multiple substitutions. In the first sequence there isan A, it's OK, in the second sequence the A mutates in C andthen in T so what we will see is only one difference, one substitution when there is actually two.
Intervention / Responsable scientifique
Thème
Documentation
Dans la même collection
-
5.7. The application domains in microbiology
RechenmannFrançoisBioinformatics relies on many domains of mathematics and computer science. Of course, algorithms themselves on character strings are important in bioinformatics, we have seen them. Algorithms and
-
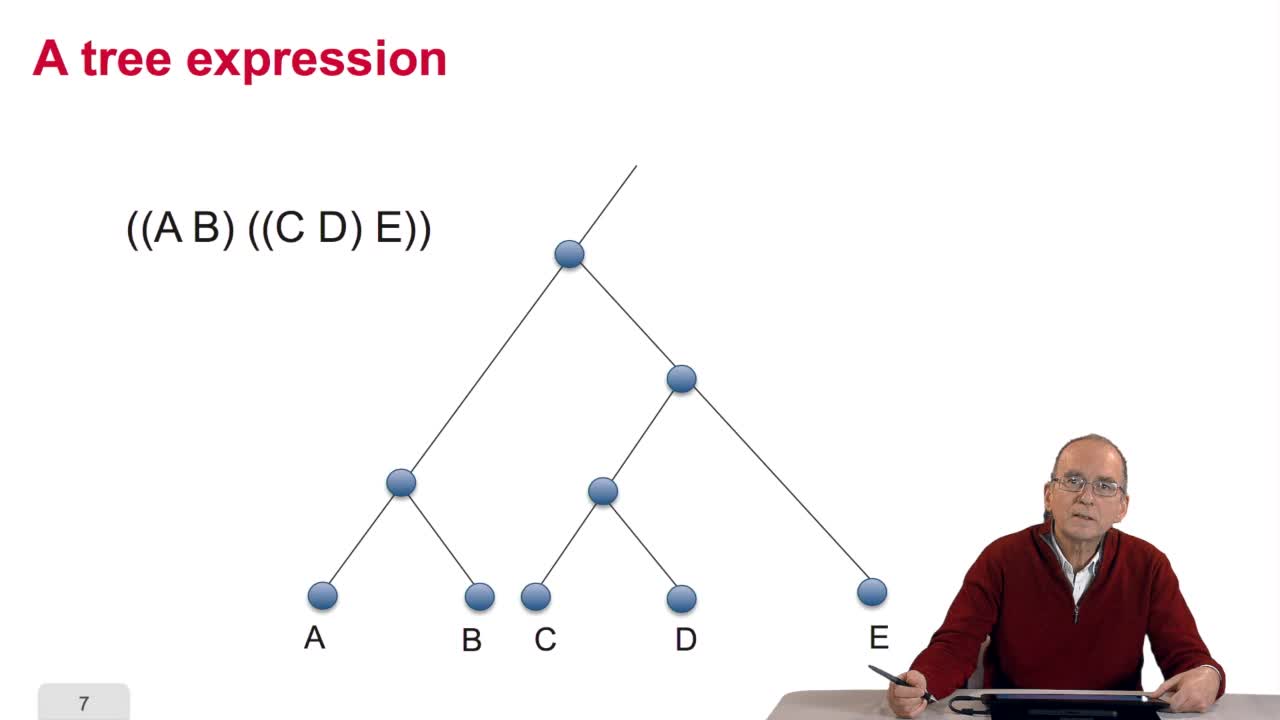
5.1. The tree of life
RechenmannFrançoisWelcome to this fifth and last week of our course on genomes and algorithms that is the computer analysis of genetic information. During this week, we will firstsee what phylogenetic trees are and how
-
5.4. The UPGMA algorithm
RechenmannFrançoisWe know how to fill an array with the values of the distances between sequences, pairs of sequences which are available in the file. This array of distances will be the input of our algorithm for
-
5.2. The tree, an abstract object
RechenmannFrançoisWhen we speak of trees, of species,of phylogenetic trees, of course, it's a metaphoric view of a real tree. Our trees are abstract objects. Here is a tree and the different components of this tree.
-
5.6. The diversity of bioinformatics algorithms
RechenmannFrançoisIn this course, we have seen a very little set of bioinformatic algorithms. There exist numerous various algorithms in bioinformatics which deal with a large span of classes of problems. For example,
-
5.3. Building an array of distances
RechenmannFrançoisSo using the sequences of homologous gene between several species, our aim is to reconstruct phylogenetic tree of the corresponding species. For this, we have to comparesequences and compute distances
Avec les mêmes intervenants et intervenantes
-
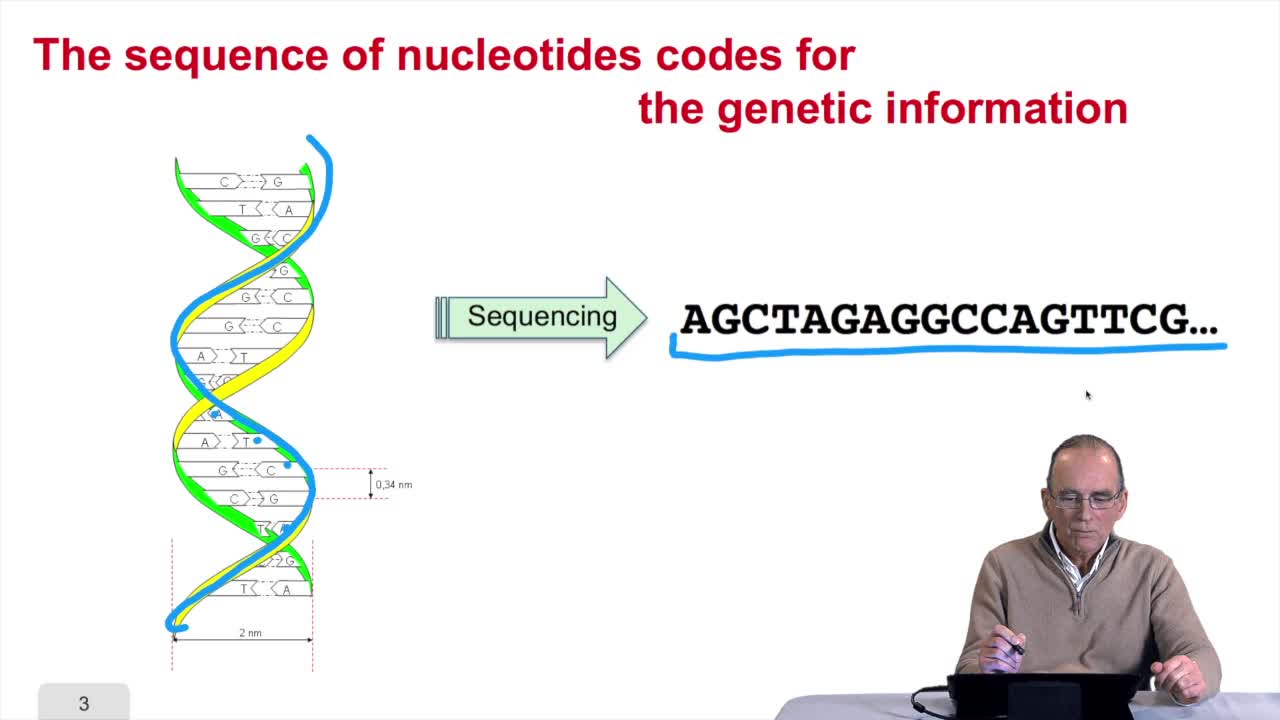
1.3. DNA codes for genetic information
RechenmannFrançoisRemember at the heart of any cell,there is this very long molecule which is called a macromolecule for this reason, which is the DNA molecule. Now we will see that DNA molecules support what is called
-
2.1. The sequence as a model of DNA
RechenmannFrançoisWelcome back to our course on genomes and algorithms that is a computer analysis ofgenetic information. Last week we introduced the very basic concept in biology that is cell, DNA, genome, genes
-
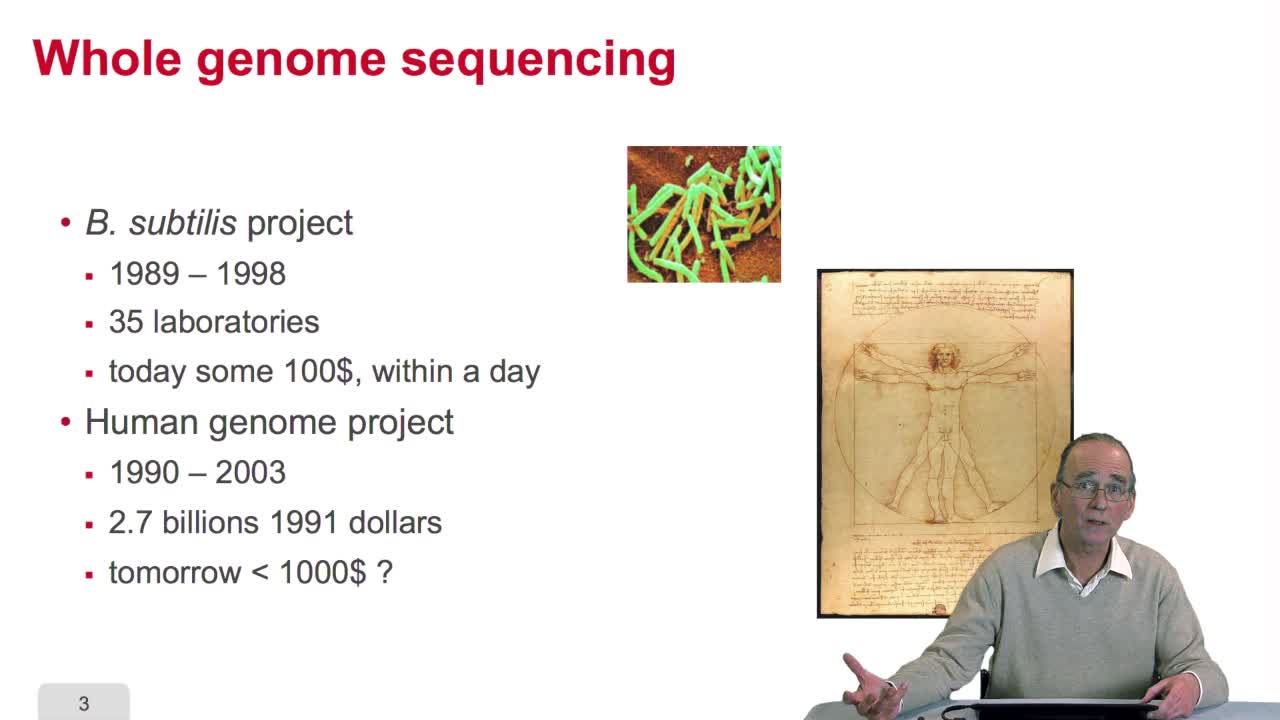
2.9. Whole genome sequencing
RechenmannFrançoisSequencing is anexponential technology. The progresses in this technologyallow now to a sequence whole genome, complete genome. What does it mean? Well let'stake two examples: some twenty years ago,
-
3.7. Index and suffix trees
RechenmannFrançoisWe have seen with the Boyer-Moore algorithm how we can increase the efficiency of spin searching through the pre-processing of the pattern to be searched. Now we will see that an alternative way of
-
4.4. Aligning sequences is an optimization problem
RechenmannFrançoisWe have seen a nice and a quitesimple solution for measuring the similarity between two sequences. It relied on the so-called hammingdistance that is counting the number of differencesbetween two
-
5.3. Building an array of distances
RechenmannFrançoisSo using the sequences of homologous gene between several species, our aim is to reconstruct phylogenetic tree of the corresponding species. For this, we have to comparesequences and compute distances
-
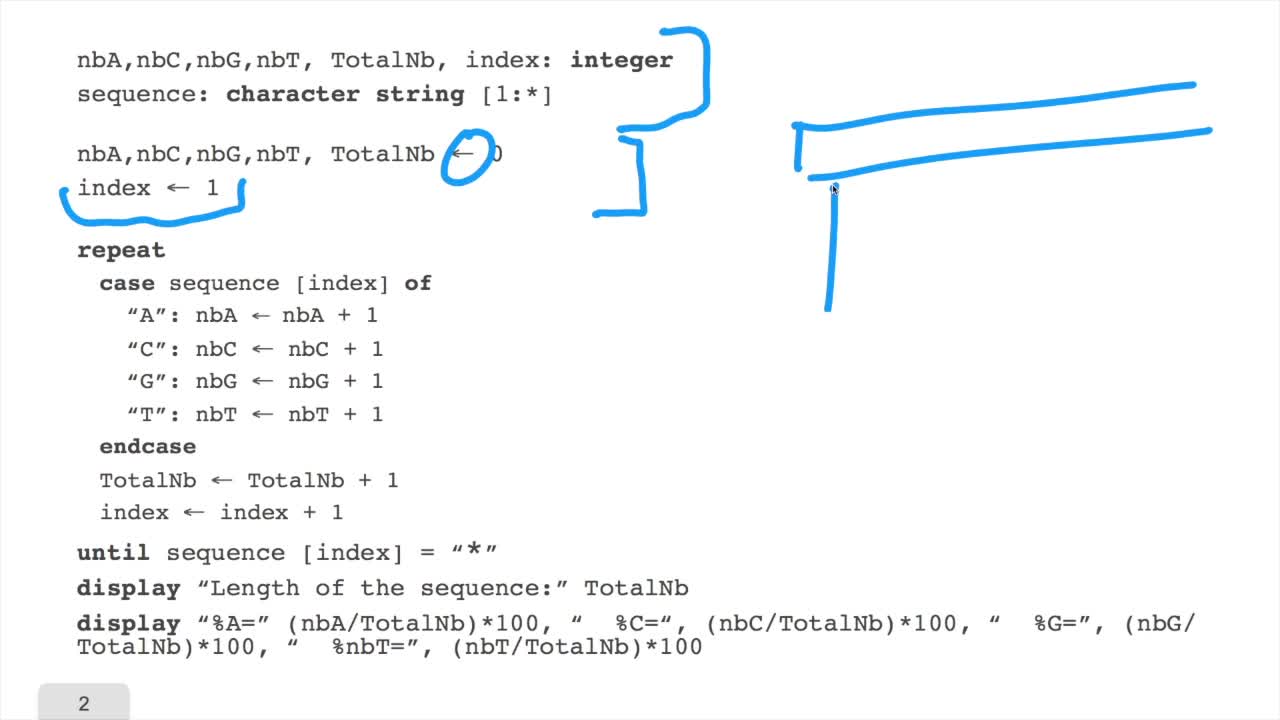
1.6. GC and AT contents of DNA sequence
RechenmannFrançoisWe have designed our first algorithmfor counting nucleotides. Remember, what we have writtenin pseudo code is first declaration of variables. We have several integer variables that are variables which
-
2.5. Implementing the genetic code
RechenmannFrançoisRemember we were designing our translation algorithm and since we are a bit lazy, we decided to make the hypothesis that there was the adequate function forimplementing the genetic code. It's now time
-
3.2. A simple algorithm for gene prediction
RechenmannFrançoisBased on the principle we statedin the last session, we will now write in pseudo code a firstalgorithm for locating genes on a bacterial genome. Remember first how this algorithm should work, we first
-
3.10. Gene prediction in eukaryotic genomes
RechenmannFrançoisIf it is possible to have verygood predictions for bacterial genes, it's certainly not the caseyet for eukaryotic genomes. Eukaryotic cells have manydifferences in comparison to prokaryotic cells. You
-
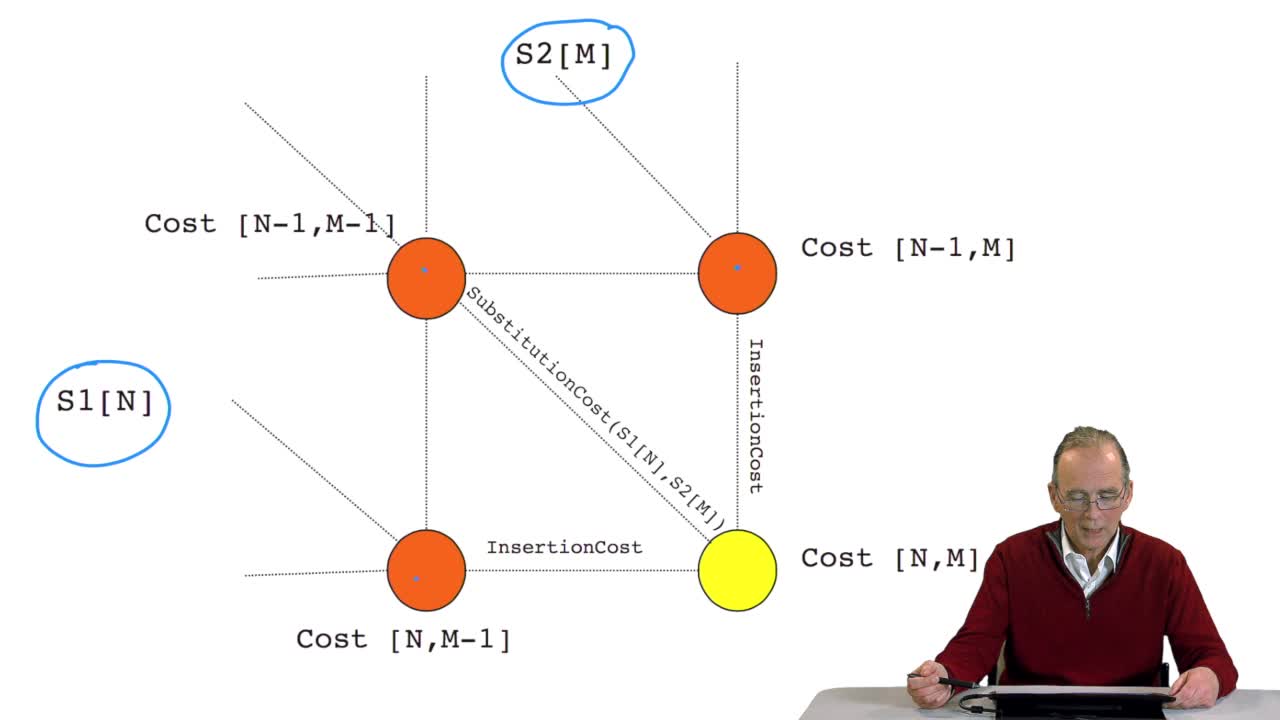
4.8. A recursive algorithm
RechenmannFrançoisWe have seen how we can computethe optimal cost, the ending node of our grid if we know the optimal cost of the three adjacent nodes. This is this computation scheme we can see here using the notation
-
5.7. The application domains in microbiology
RechenmannFrançoisBioinformatics relies on many domains of mathematics and computer science. Of course, algorithms themselves on character strings are important in bioinformatics, we have seen them. Algorithms and