Notice
5.4. The UPGMA algorithm
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
We know how to fill an array with the values of the distances between sequences, pairs of sequences which are available in the file. This array of distances will be the input of our algorithm for reconstructing phylogenetic trees. The name of this algorithm israther complicated but the method itself is rather simple,too simple indeed. We will see that. The name standsfor Unweighted Pair Group Method with Arithmetic Mean, wewill understand these terms along the presentationof the algorithm. The algorithm starts withan array of distances. Let's take this very simpleexample, it implies seven species and here we have the values of thedistances between these different sequences associated with a species. As you remember, the array issymmetrical and all the values on the diagonal are equal to zero so here we display only the meaning ful values. So all the cells of the array are not displayed here. OK. First step consists in selectingthe smallest value of the array, this is two here which isthe distance between F and C. So since it is the smallest distance we allow to group these two species, these two nodes into a first sub tree and create a new node here which is the route of this sub tree.
Thème
Documentation
Dans la même collection
-
5.2. The tree, an abstract object
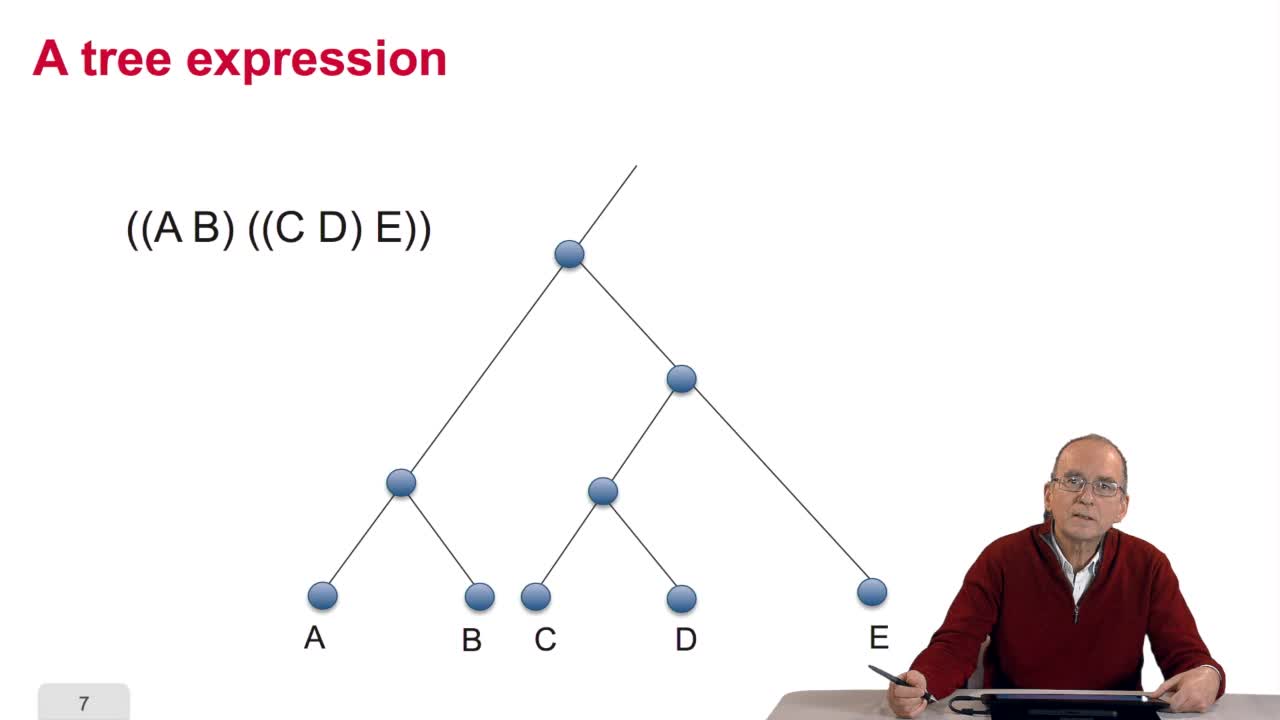
RechenmannFrançoisWhen we speak of trees, of species,of phylogenetic trees, of course, it's a metaphoric view of a real tree. Our trees are abstract objects. Here is a tree and the different components of this tree.
-
5.6. The diversity of bioinformatics algorithms
RechenmannFrançoisIn this course, we have seen a very little set of bioinformatic algorithms. There exist numerous various algorithms in bioinformatics which deal with a large span of classes of problems. For example,
-
5.3. Building an array of distances
RechenmannFrançoisSo using the sequences of homologous gene between several species, our aim is to reconstruct phylogenetic tree of the corresponding species. For this, we have to comparesequences and compute distances
-
5.7. The application domains in microbiology
RechenmannFrançoisBioinformatics relies on many domains of mathematics and computer science. Of course, algorithms themselves on character strings are important in bioinformatics, we have seen them. Algorithms and
-
5.1. The tree of life
RechenmannFrançoisWelcome to this fifth and last week of our course on genomes and algorithms that is the computer analysis of genetic information. During this week, we will firstsee what phylogenetic trees are and how
-
5.5. Differences are not always what they look like
RechenmannFrançoisThe algorithm we have presented works on an array of distance between sequences. These distances are evaluated on the basis of differences between the sequences. The problem is that behind the
Avec les mêmes intervenants et intervenantes
-
1.7. DNA walk
RechenmannFrançoisWe will now design a more graphical algorithm which is called "the DNA walk". We shall see what does it mean "DNA walk". Walk on to DNA. Something like that, yes. But first, just have a look again at
-
2.6. Algorithms + data structures = programs
RechenmannFrançoisBy writing the Lookup GeneticCode Function, we completed our translation algorithm. So we may ask the question about the algorithm, does it terminate? Andthe answer is yes, obviously. Is it pertinent,
-
3.3. Searching for start and stop codons
RechenmannFrançoisWe have written an algorithm for finding genes. But you remember that we arestill to write the two functions for finding the next stop codonand the next start codon. Let's see how we can do that. We
-
4.1. How to predict gene/protein functions?
RechenmannFrançoisLast week we have seen that annotating a genome means first locating the genes on the DNA sequences that is the genes, the region coding for proteins. But this is indeed the first step,the next very
-
4.10. How efficient is this algorithm?
RechenmannFrançoisWe have seen the principle of an iterative algorithm in two paths for aligning and comparing two sequences of characters, here DNA sequences. And we understoodwhy the iterative version is much more
-
1.2. At the heart of the cell: the DNA macromolecule
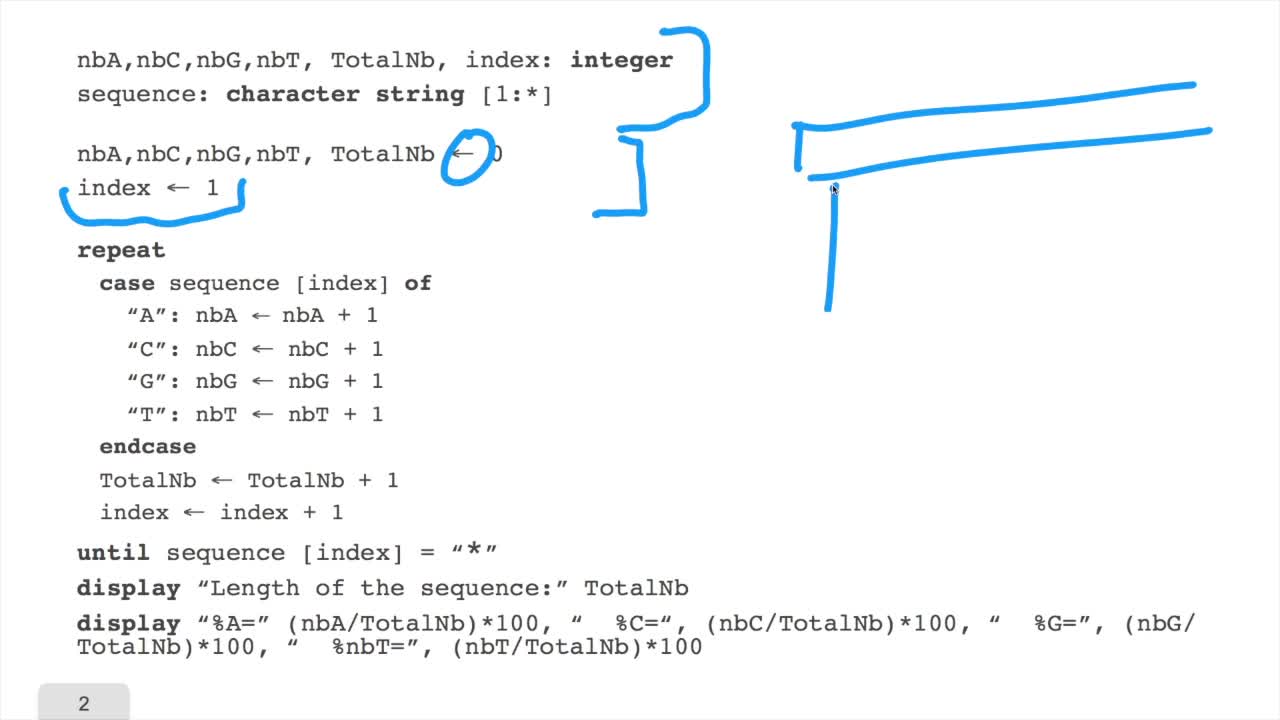
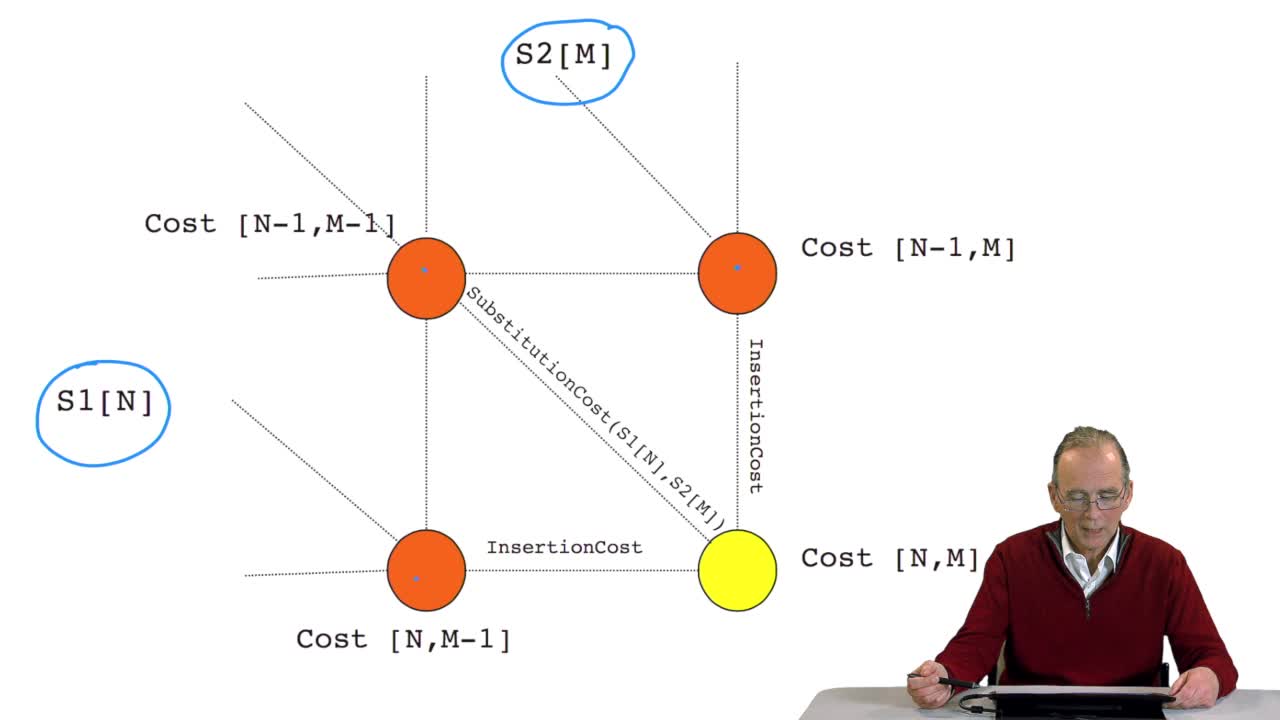
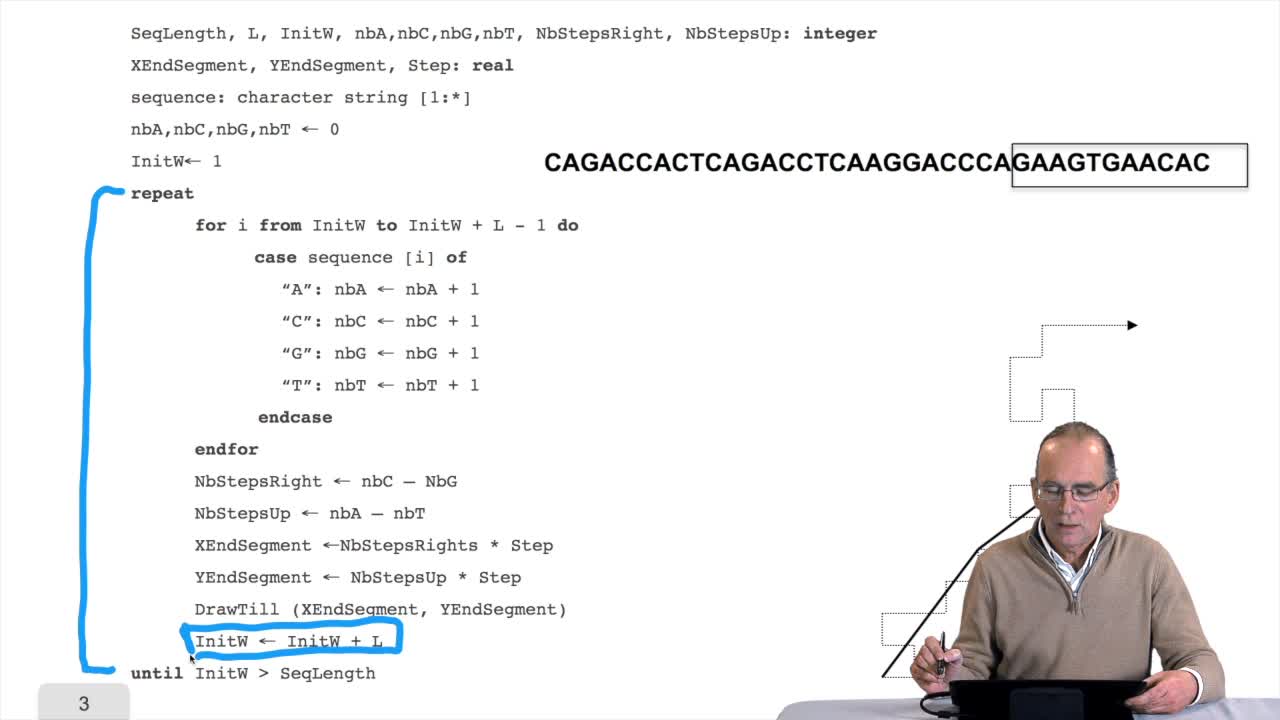
RechenmannFrançoisDuring the last session, we saw how at the heart of the cell there's DNA in the nucleus, sometimes of cells, or directly in the cytoplasm of the bacteria. The DNA is what we call a macromolecule, that
-
1.10. Overlapping sliding window
RechenmannFrançoisWe have made some drawings along a genomic sequence. And we have seen that although the algorithm is quite simple, even if some points of the algorithmare bit trickier than the others, we were able to
-
2.3. The genetic code
RechenmannFrançoisGenes code for proteins. What is the correspondence betweenthe genes, DNA sequences, and the structure of proteins? The correspondence isthe genetic code. Proteins have indeedsequences of amino acids.
-
3.6. Boyer-Moore algorithm
RechenmannFrançoisWe have seen how we can make gene predictions more reliable through searching for all the patterns,all the occurrences of patterns. We have seen, for example, howif we locate the RBS, Ribosome
-
4.5. A sequence alignment as a path
RechenmannFrançoisComparing two sequences and thenmeasuring their similarities is an optimization problem. Why? Because we have seen thatwe have to take into account substitution and deletion. During the alignment, the
-
5.5. Differences are not always what they look like
RechenmannFrançoisThe algorithm we have presented works on an array of distance between sequences. These distances are evaluated on the basis of differences between the sequences. The problem is that behind the
-
1.5. Counting nucleotides
RechenmannFrançoisIn this session, don't panic. We will design our first algorithm. This algorithm is forcounting nucleotides. The idea here is that as an input,you have a sequence of nucleotides, of bases, of letters,
