Notice
5.7. The application domains in microbiology
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
Bioinformatics relies on many domains of mathematics and computer science. Of course, algorithms themselves on character strings are important in bioinformatics, we have seen them. Algorithms and trees, for example,for reconstructing phylogenetic trees, algorithms on networks toreconstruct gene interaction networks, metabolic networks and maybe to simulate the dynamics of the time. We have seen also the implicationof probability and statistics. The implication of optimizationmethods, for example, for the computation of the optimalalignment of a pair of sequences. Constraint satisfaction is used forpredicting molecule structure. Automata and formal grammarswhich are some exotic parts of computer science are also usefulin bioinformatics, the same for signal processing. And soother domains may be listed here. We also have to understand that designing an algorithm is something but implementing the algorithm asa working software is another part of the story. So after the algorithm design, we have to think in terms of software development,in terms of user interfaces and especially for data visualization and of course in terms of database, conception design and maintenance. This software and database are the tools which can be used in various application domainsof bioinformatics.
Intervention / Responsable scientifique
Thème
Documentation
Dans la même collection
-
5.6. The diversity of bioinformatics algorithms
RechenmannFrançoisIn this course, we have seen a very little set of bioinformatic algorithms. There exist numerous various algorithms in bioinformatics which deal with a large span of classes of problems. For example,
-
5.1. The tree of life
RechenmannFrançoisWelcome to this fifth and last week of our course on genomes and algorithms that is the computer analysis of genetic information. During this week, we will firstsee what phylogenetic trees are and how
-
5.4. The UPGMA algorithm
RechenmannFrançoisWe know how to fill an array with the values of the distances between sequences, pairs of sequences which are available in the file. This array of distances will be the input of our algorithm for
-
5.2. The tree, an abstract object
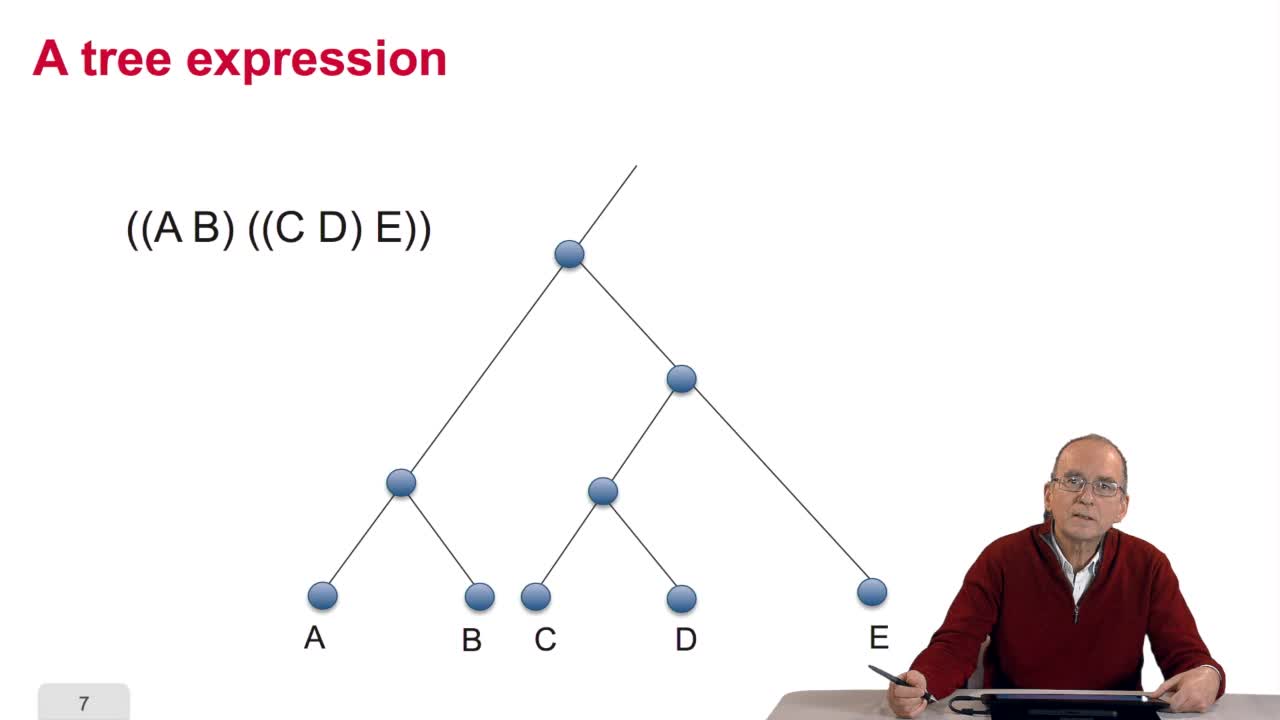
RechenmannFrançoisWhen we speak of trees, of species,of phylogenetic trees, of course, it's a metaphoric view of a real tree. Our trees are abstract objects. Here is a tree and the different components of this tree.
-
5.5. Differences are not always what they look like
RechenmannFrançoisThe algorithm we have presented works on an array of distance between sequences. These distances are evaluated on the basis of differences between the sequences. The problem is that behind the
-
5.3. Building an array of distances
RechenmannFrançoisSo using the sequences of homologous gene between several species, our aim is to reconstruct phylogenetic tree of the corresponding species. For this, we have to comparesequences and compute distances
Avec les mêmes intervenants et intervenantes
-
1.6. GC and AT contents of DNA sequence
RechenmannFrançoisWe have designed our first algorithmfor counting nucleotides. Remember, what we have writtenin pseudo code is first declaration of variables. We have several integer variables that are variables which
-
2.5. Implementing the genetic code
RechenmannFrançoisRemember we were designing our translation algorithm and since we are a bit lazy, we decided to make the hypothesis that there was the adequate function forimplementing the genetic code. It's now time
-
3.2. A simple algorithm for gene prediction
RechenmannFrançoisBased on the principle we statedin the last session, we will now write in pseudo code a firstalgorithm for locating genes on a bacterial genome. Remember first how this algorithm should work, we first
-
3.10. Gene prediction in eukaryotic genomes
RechenmannFrançoisIf it is possible to have verygood predictions for bacterial genes, it's certainly not the caseyet for eukaryotic genomes. Eukaryotic cells have manydifferences in comparison to prokaryotic cells. You
-
4.8. A recursive algorithm
RechenmannFrançoisWe have seen how we can computethe optimal cost, the ending node of our grid if we know the optimal cost of the three adjacent nodes. This is this computation scheme we can see here using the notation
-
5.6. The diversity of bioinformatics algorithms
RechenmannFrançoisIn this course, we have seen a very little set of bioinformatic algorithms. There exist numerous various algorithms in bioinformatics which deal with a large span of classes of problems. For example,
-
1.1. The cell, atom of the living world
RechenmannFrançoisWelcome to this introduction to bioinformatics. We will speak of genomes and algorithms. More specifically, we will see how genetic information can be analysed by algorithms. In these five weeks to
-
1.9. Predicting the origin of DNA replication?
RechenmannFrançoisWe have seen a nice algorithm to draw, let's say, a DNA sequence. We will see that first, we have to correct a little bit this algorithm. And then we will see how such as imple algorithm can provide
-
2.8. DNA sequencing
RechenmannFrançoisDuring the last session, I explained several times how it was important to increase the efficiency of sequences processing algorithm because sequences arevery long and there are large volumes of
-
3.5. Making the predictions more reliable
RechenmannFrançoisWe have got a bacterial gene predictor but the way this predictor works is rather crude and if we want to have more reliable results, we have to inject into this algorithmmore biological knowledge. We
-
4.6. A path is optimal if all its sub-paths are optimal
RechenmannFrançoisA sequence alignment between two sequences is a path in a grid. So that, an optimal sequence alignmentis an optimal path in the same grid. We'll see now that a property of this optimal path provides
-
5.1. The tree of life
RechenmannFrançoisWelcome to this fifth and last week of our course on genomes and algorithms that is the computer analysis of genetic information. During this week, we will firstsee what phylogenetic trees are and how
