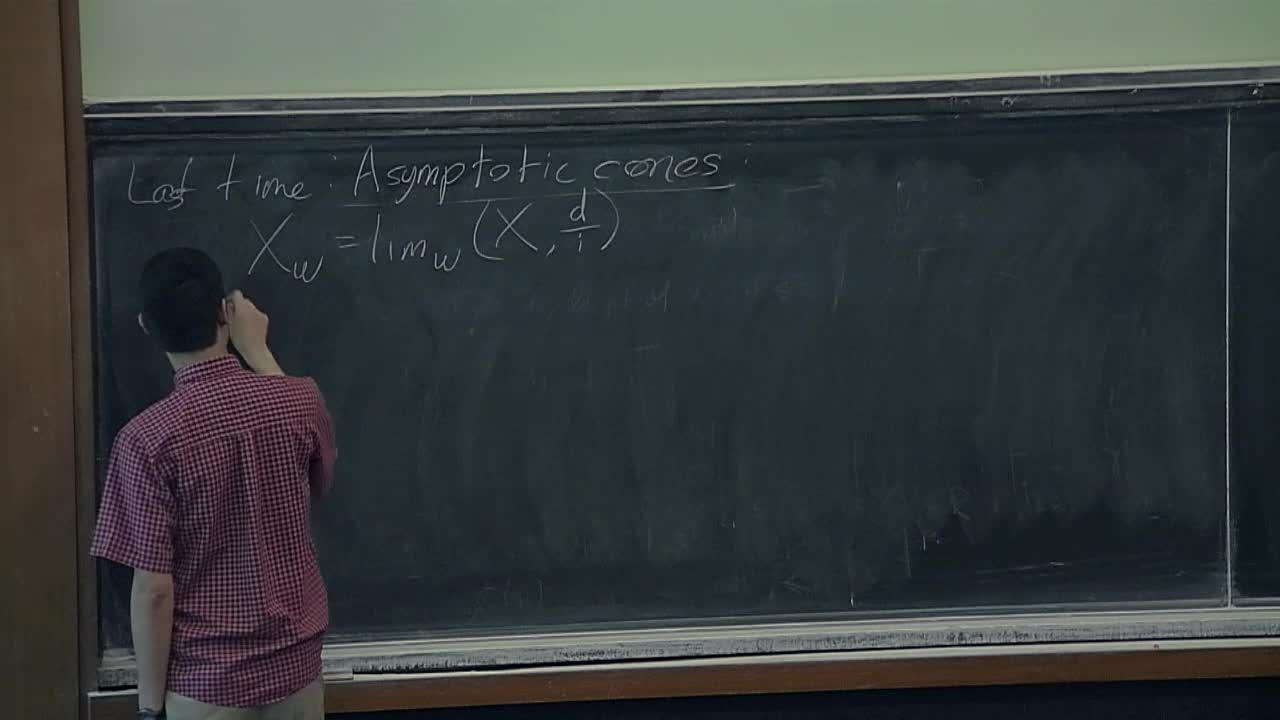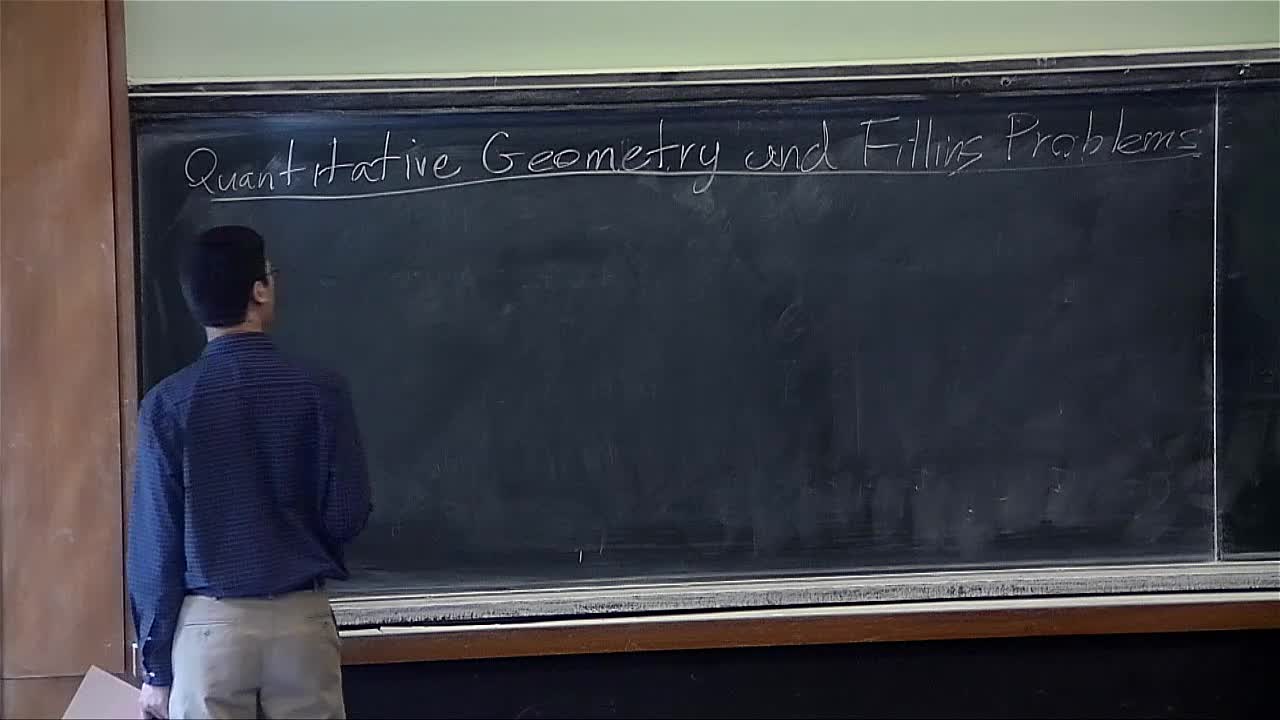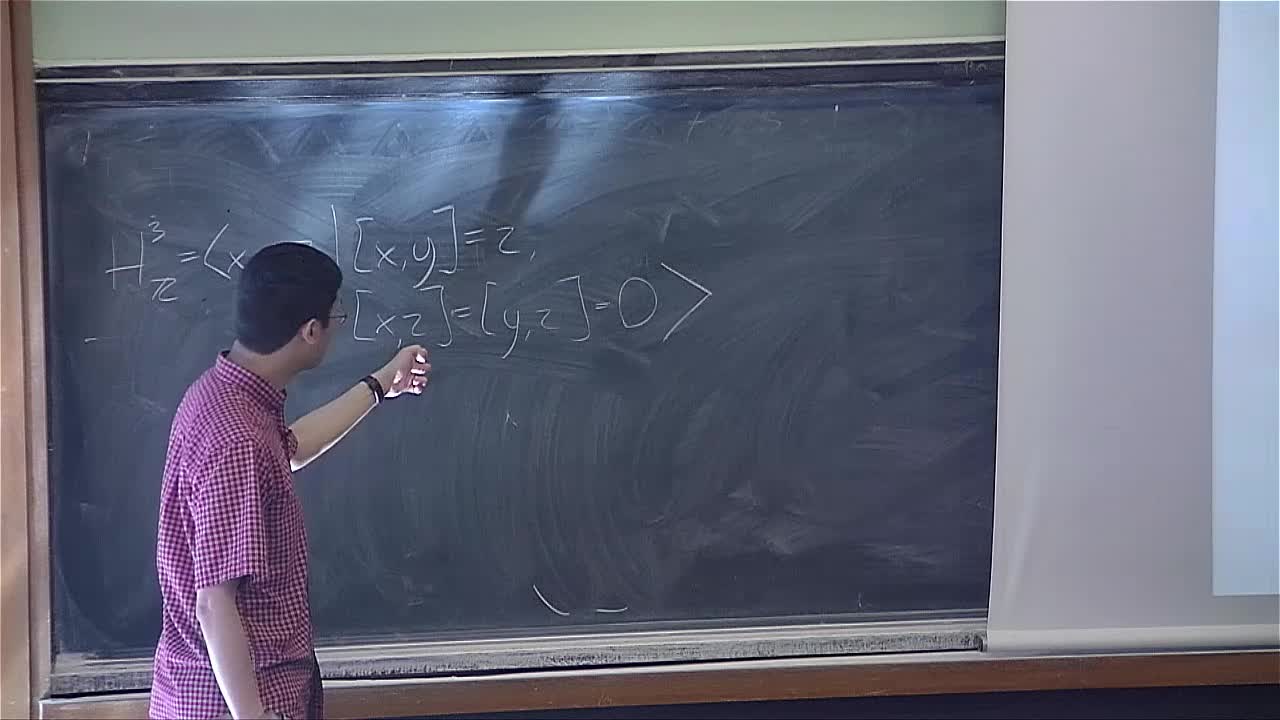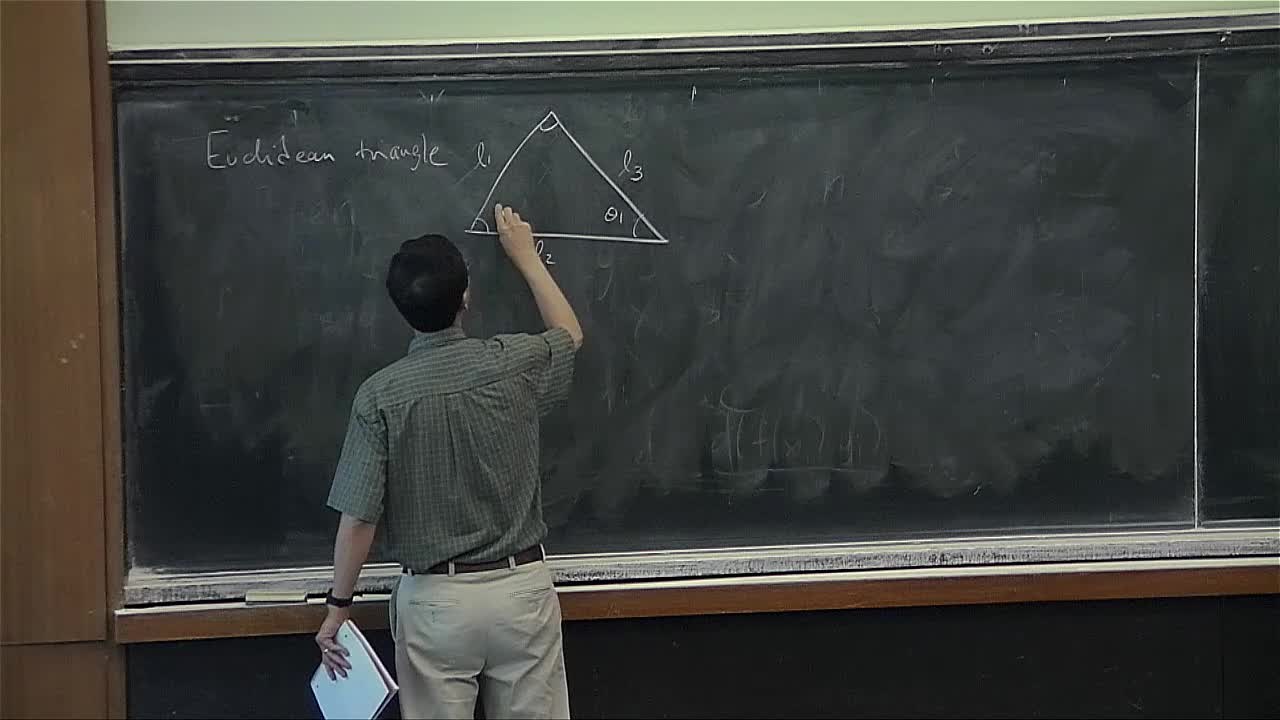Notice
Feng Luo - An introduction to discrete conformal geometry of polyhedral surfaces (Part 1)
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
The goal of the course is to introduce some of the recent developments on discrete conformal geometry of polyhedral surfaces. We plan to cover the following topics.
- The Andreev-Koebe-Thurston theorem on circle packing polyhedral metrics and Marden-Rodin’s proof
- Thurston’s conjecture on the convergence of circle packings to the Riemann mapping and its solution by Rodin-Sullivan
- Finite dimensional variational principles associated to polyhedral surfaces
- A discrete conformal equivalence of polyhedral surfaces and its relationship to convex polyhedra in hyperbolic 3-space
- A discrete uniformization theorem for compact polyhedral surfaces
- Convergence of discrete conformality and some open problems
Thème
Dans la même collection
-
Robert Young - Quantitative geometry and filling problems (Part 1)
Plateau's problem asks whether there exists a minimal surface with a given boundary in Euclidean space. In this course, we will study related problems in broader classes of spaces and ask what the
-
Robert Young - Quantitative geometry and filling problems (Part 3)
Plateau's problem asks whether there exists a minimal surface with a given boundary in Euclidean space. In this course, we will study related problems in broader classes of spaces and ask what the
-
Robert Young - Quantitative geometry and filling problems (Part 5)
Plateau's problem asks whether there exists a minimal surface with a given boundary in Euclidean space. In this course, we will study related problems in broader classes of spaces and ask what the
-
Robert Young - Quantitative geometry and filling problems (Part 2)
Plateau's problem asks whether there exists a minimal surface with a given boundary in Euclidean space. In this course, we will study related problems in broader classes of spaces and ask what the
-
Robert Young - Quantitative geometry and filling problems (Part 4)
Plateau's problem asks whether there exists a minimal surface with a given boundary in Euclidean space. In this course, we will study related problems in broader classes of spaces and ask what the
-
Feng Luo - An introduction to discrete conformal geometry of polyhedral surfaces (Part 2)
LuoFengThe goal of the course is to introduce some of the recent developments on discrete conformal geometry of polyhedral surfaces. We plan to cover the following topics. - The Andreev-Koebe-Thurston
-
Sylvain Maillot - An introduction to open 3-manifolds (Part 1)
MaillotSylvainW. Thurston's geometrization program has lead to manyoutstanding results in 3-manifold theory. Thanks to worksof G. Perelman, J. Kahn and V. Markovic, D. Wise, and I. Agol among others, compact 3
-
Feng Luo - An introduction to discrete conformal geometry of polyhedral surfaces (Part 4)
LuoFengThe goal of the course is to introduce some of the recent developments on discrete conformal geometry of polyhedral surfaces. We plan to cover the following topics. - The Andreev-Koebe-Thurston
-
Sylvain Maillot - An introduction to open 3-manifolds (Part 4)
MaillotSylvainW. Thurston's geometrization program has lead to manyoutstanding results in 3-manifold theory. Thanks to worksof G. Perelman, J. Kahn and V. Markovic, D. Wise, and I. Agol among others, compact 3
-
Sylvain Maillot - An introduction to open 3-manifolds (Part 2)
MaillotSylvainW. Thurston's geometrization program has lead to manyoutstanding results in 3-manifold theory. Thanks to worksof G. Perelman, J. Kahn and V. Markovic, D. Wise, and I. Agol among others, compact 3
-
Feng Luo - An introduction to discrete conformal geometry of polyhedral surfaces (Part 3)
LuoFengThe goal of the course is to introduce some of the recent developments on discrete conformal geometry of polyhedral surfaces. We plan to cover the following topics. - The Andreev-Koebe-Thurston
-
Sylvain Maillot - An introduction to open 3-manifolds (Part 3)
MaillotSylvainW. Thurston's geometrization program has lead to manyoutstanding results in 3-manifold theory. Thanks to worksof G. Perelman, J. Kahn and V. Markovic, D. Wise, and I. Agol among others, compact 3
Avec les mêmes intervenants et intervenantes
-
Feng Luo - An introduction to discrete conformal geometry of polyhedral surfaces (Part 5)
LuoFengThe goal of the course is to introduce some of the recent developments on discrete conformal geometry of polyhedral surfaces. We plan to cover the following topics. - The Andreev-Koebe-Thurston
-
Feng Luo - An introduction to discrete conformal geometry of polyhedral surfaces (Part 3)
LuoFengThe goal of the course is to introduce some of the recent developments on discrete conformal geometry of polyhedral surfaces. We plan to cover the following topics. - The Andreev-Koebe-Thurston
-
Feng Luo - An introduction to discrete conformal geometry of polyhedral surfaces (Part 4)
LuoFengThe goal of the course is to introduce some of the recent developments on discrete conformal geometry of polyhedral surfaces. We plan to cover the following topics. - The Andreev-Koebe-Thurston
-
Feng Luo - An introduction to discrete conformal geometry of polyhedral surfaces (Part 2)
LuoFengThe goal of the course is to introduce some of the recent developments on discrete conformal geometry of polyhedral surfaces. We plan to cover the following topics. - The Andreev-Koebe-Thurston
-
Feng Luo - Discrete conformal geometry of polyhedral surfaces and its convergence
LuoFengOur recent joint work with D. Gu established a discrete version of the uniformization theorem for compact polyhedral surfaces. In this talk, we prove that discrete uniformizaton maps converge to
Sur le même thème
-
"Le mathématicien Petre (Pierre) Sergescu, historien des sciences, personnalité du XXe siècle"
HerléaAlexandreAlexandre HERLEA est membre de la section « Sciences, histoire des sciences et des techniques et archéologie industrielle » du CTHS. Professeur émérite des universités, membre effectif de l'Académie
-
Webinaire sur la rédaction des PGD
LouvetViolaineRédaction des Plans de Gestion de Données (PGD) sous l’angle des besoins de la communauté mathématique.
-
Alexandre Booms : « Usage de matériel pédagogique adapté en géométrie : une transposition à interro…
« Usage de matériel pédagogique adapté en géométrie : une transposition à interroger ». Alexandre Booms, doctorant (Université de Reims Champagne-Ardenne - Cérep UR 4692)
-
P. Burkhardt - Pointwise lower scalar curvature bounds for C0 metrics via regularizing Ricci flow
Burkhardt-GuimPaulaWe propose a class of local definitions of weak lower scalar curvature bounds that is well defined for C0 metrics. We show the following: that our definitions are stable under greater-than-second
-
R. Bamler - Compactness and partial regularity theory of Ricci flows in higher dimensions
BamlerRichard H.We present a new compactness theory of Ricci flows. This theory states that any sequence of Ricci flows that is pointed in an appropriate sense, subsequentially converges to a synthetic flow.
-
C. Li - Classifying sufficiently connected PSC manifolds in 4 and 5 dimensions
LiChaoIn this talk, I will discuss some recent developments on the topology of closed manifolds admitting Riemannian metrics of positive scalar curvature. In particular, we will prove if a closed PSC
-
Y. Lai - A family of 3d steady gradient Ricci solitons that are flying wings
LaiYiWe find a family of 3d steady gradient Ricci solitons that are flying wings. This verifies a conjecture by Hamilton. For a 3d flying wing, we show that the scalar curvature does not vanish at
-
T. Ozuch - Noncollapsed degeneration and desingularization of Einstein 4-manifolds
OzuchTristanWe study the noncollapsed singularity formation of Einstein 4-manifolds. We prove that any smooth Einstein 4-manifold close to a singular one in a mere Gromov-Hausdorff (GH) sense is the result
-
D. Tewodrose - Limits of Riemannian manifolds satisfying a uniform Kato condition
TewodroseDavidPresentation of a joint work with G. Carron and I. Mondello where we study Kato limit spaces.
-
A. Mondino - Time-like Ricci curvature bounds via optimal transport
MondinoAndreaThe goal of the talk is to present a recent work in collaboration with Cavalletti (SISSA) on optimal transport in Lorentzian synthetic spaces. The aim is to set up a “Lorentzian analog” of the
-
M. Lesourd - Positive Scalar Curvature on Noncompact Manifolds and the Positive Mass Theorem
LesourdMartinThe study of positive scalar curvature on noncompact manifolds has seen significant progress in the last few years. A major role has been played by Gromov's results and conjectures, and in
-
J. Wang - Topological rigidity and positive scalar curvature
WangJianIn this talk, we shall describe some topological rigidity and its relationship with positive scalar curvature. Precisely, we will present a proof that a complete contractible 3-manifold with
