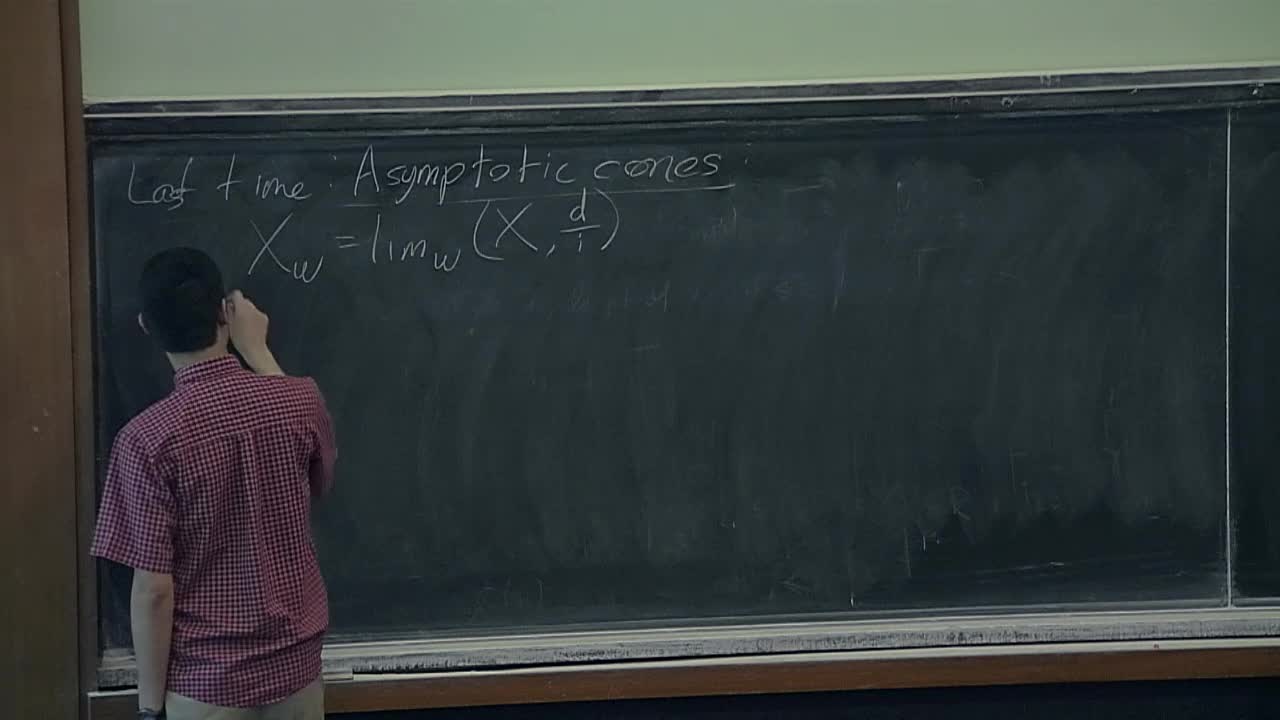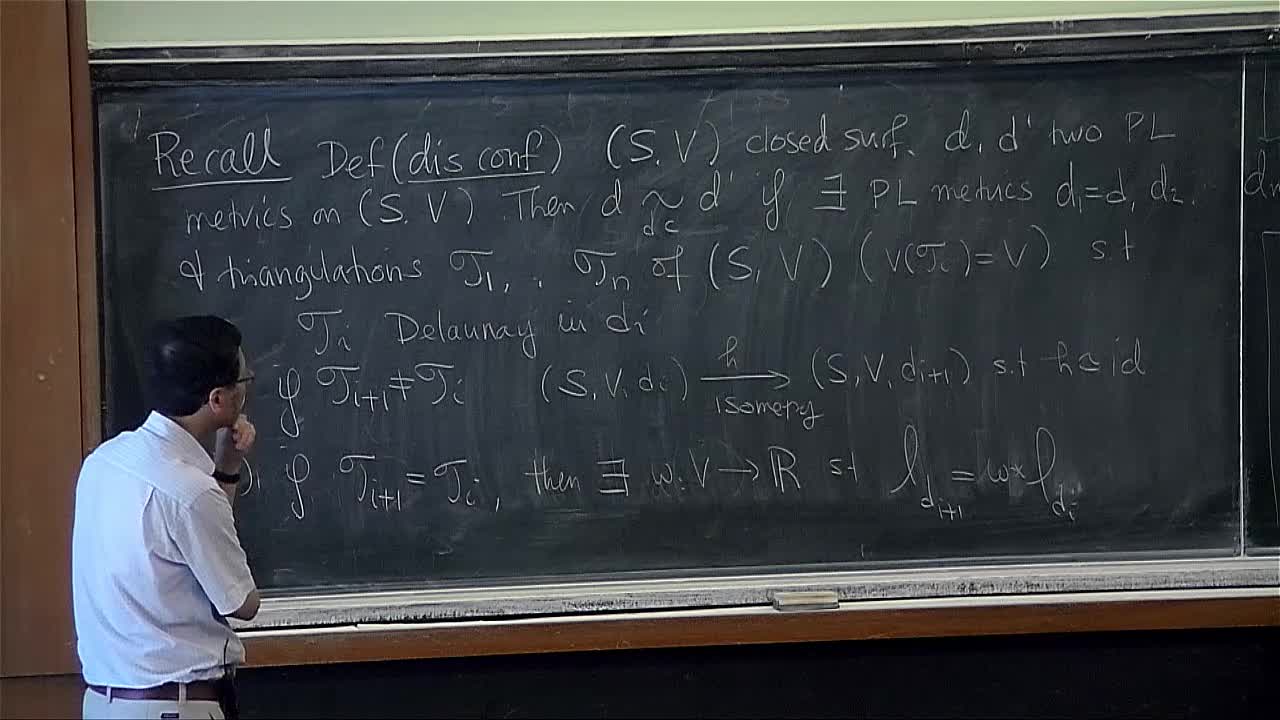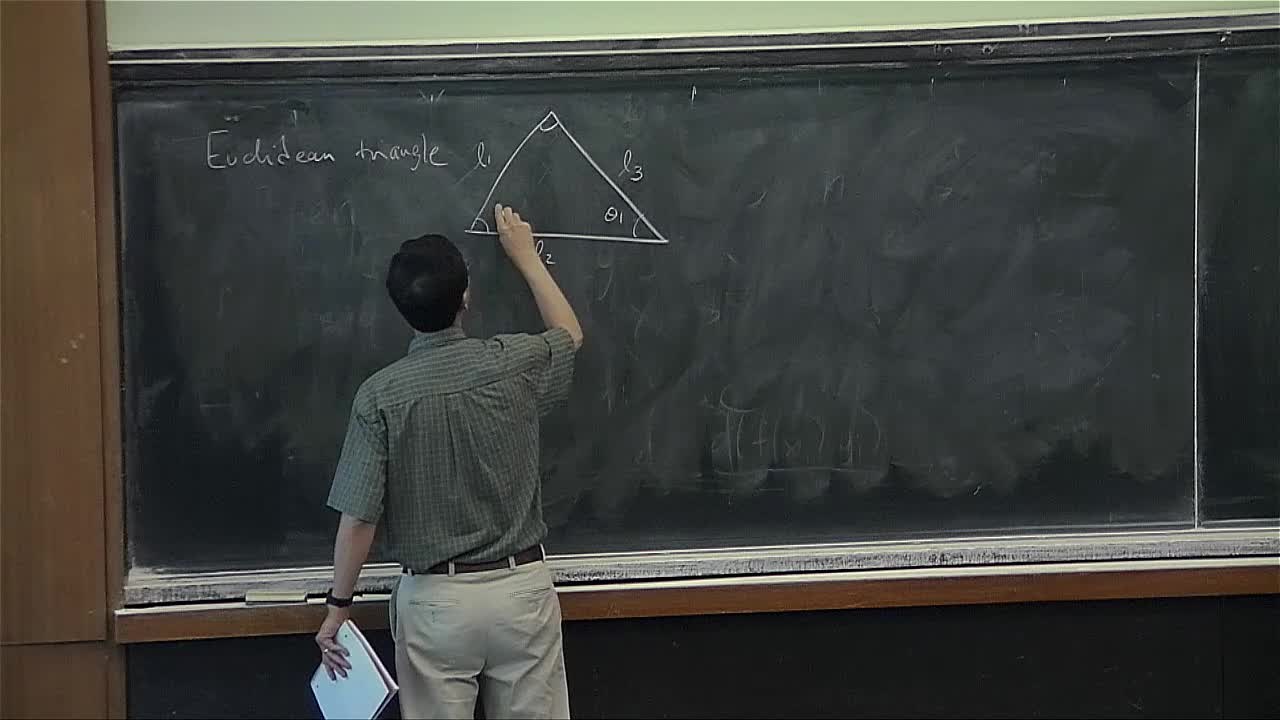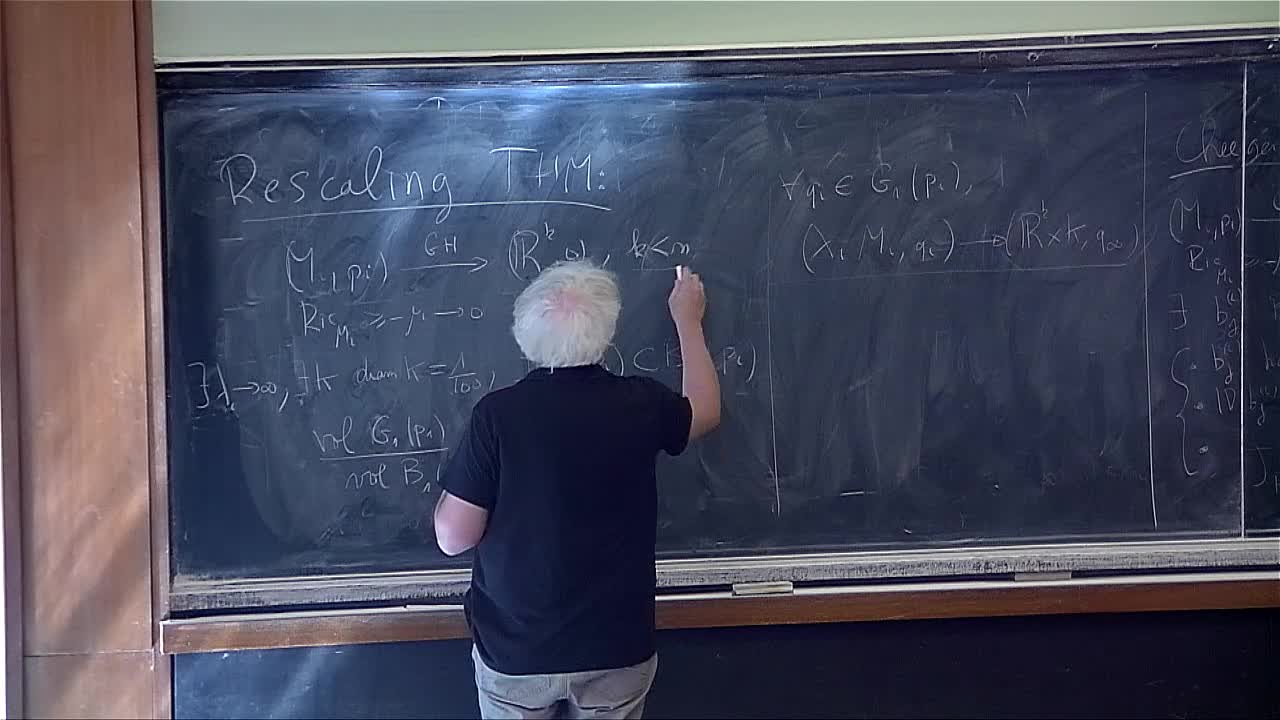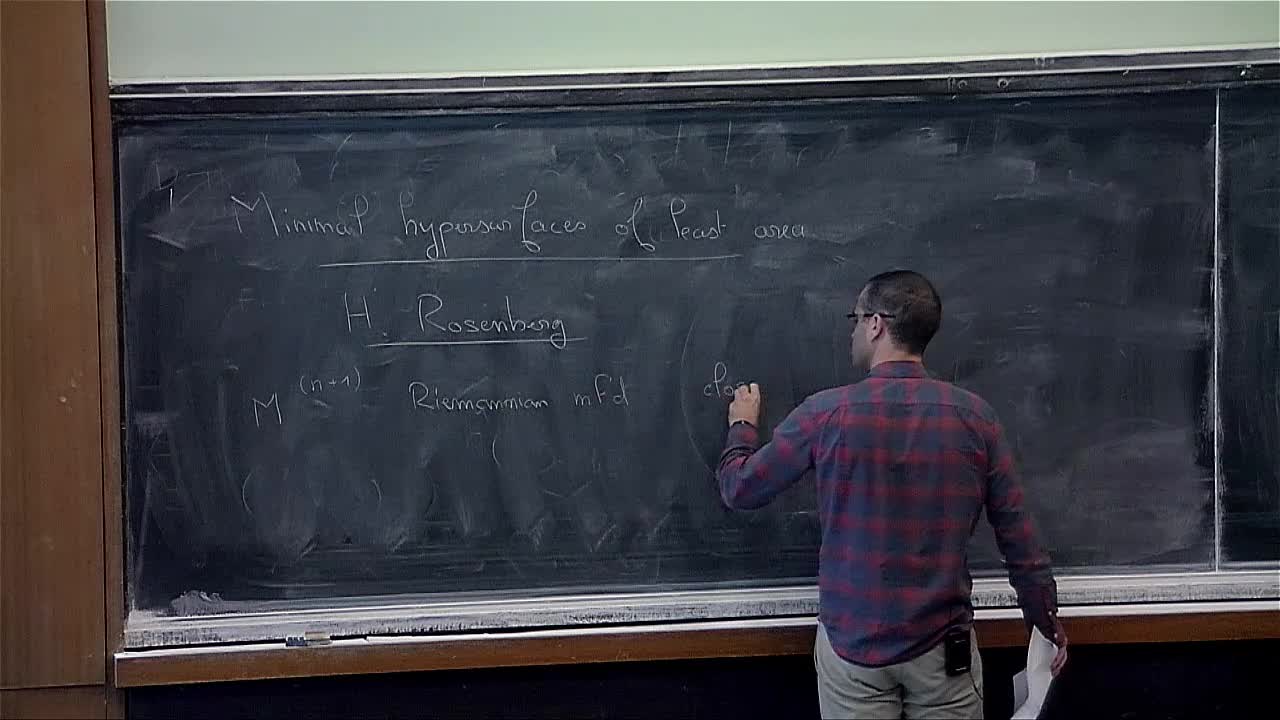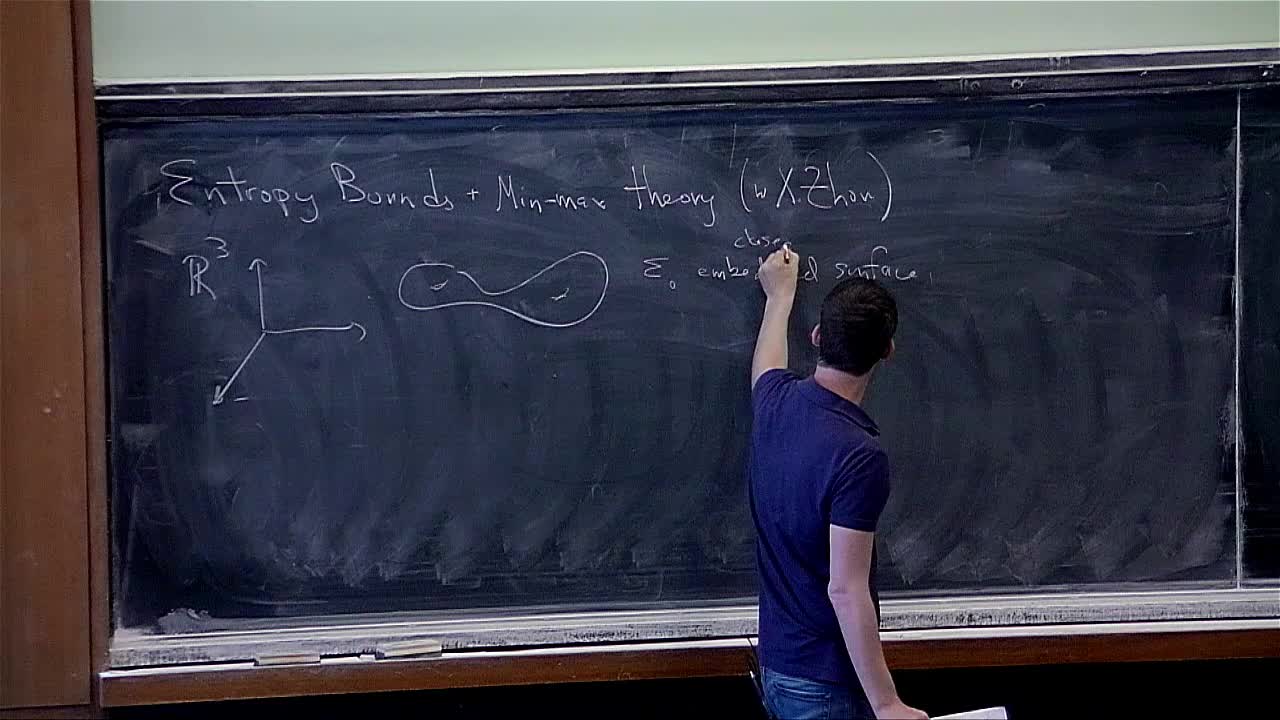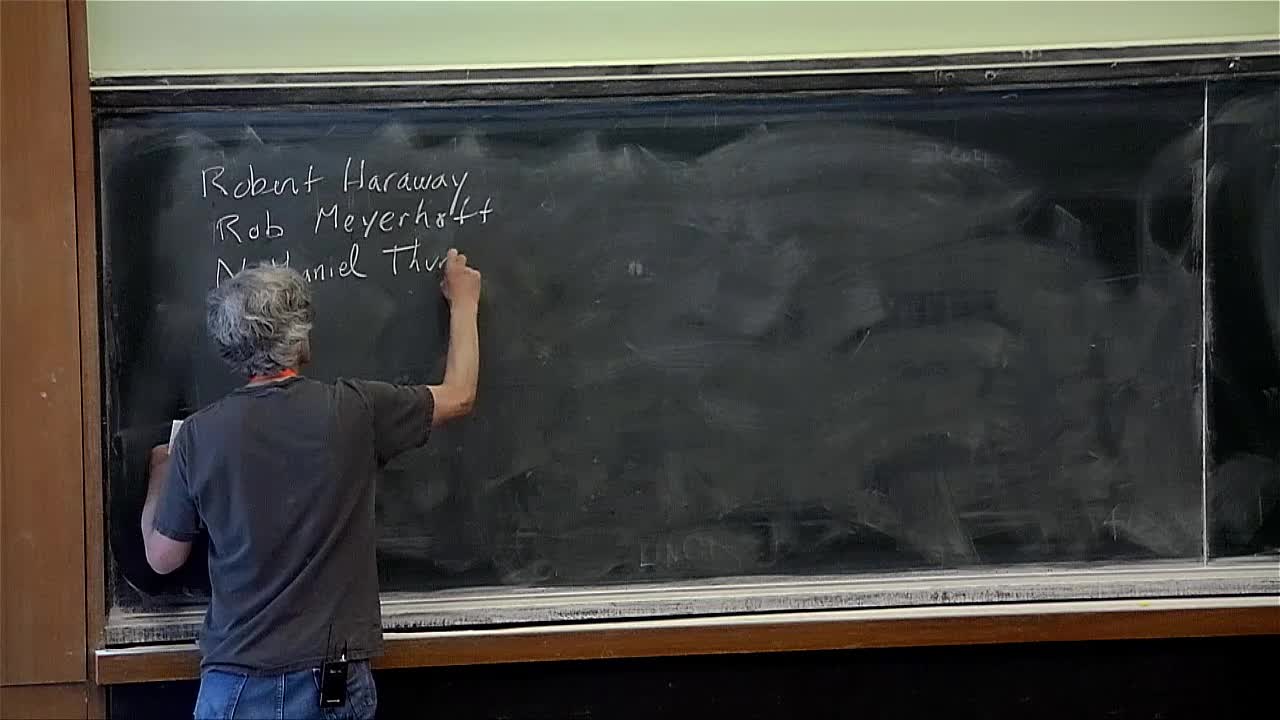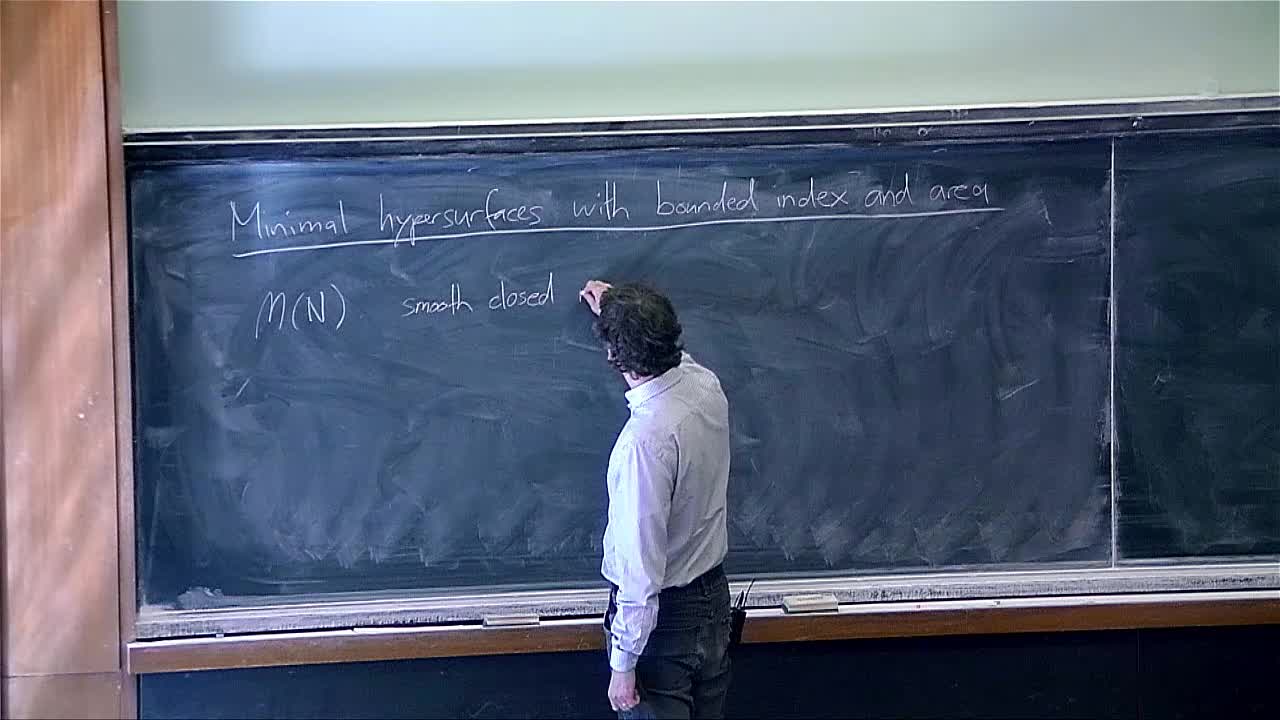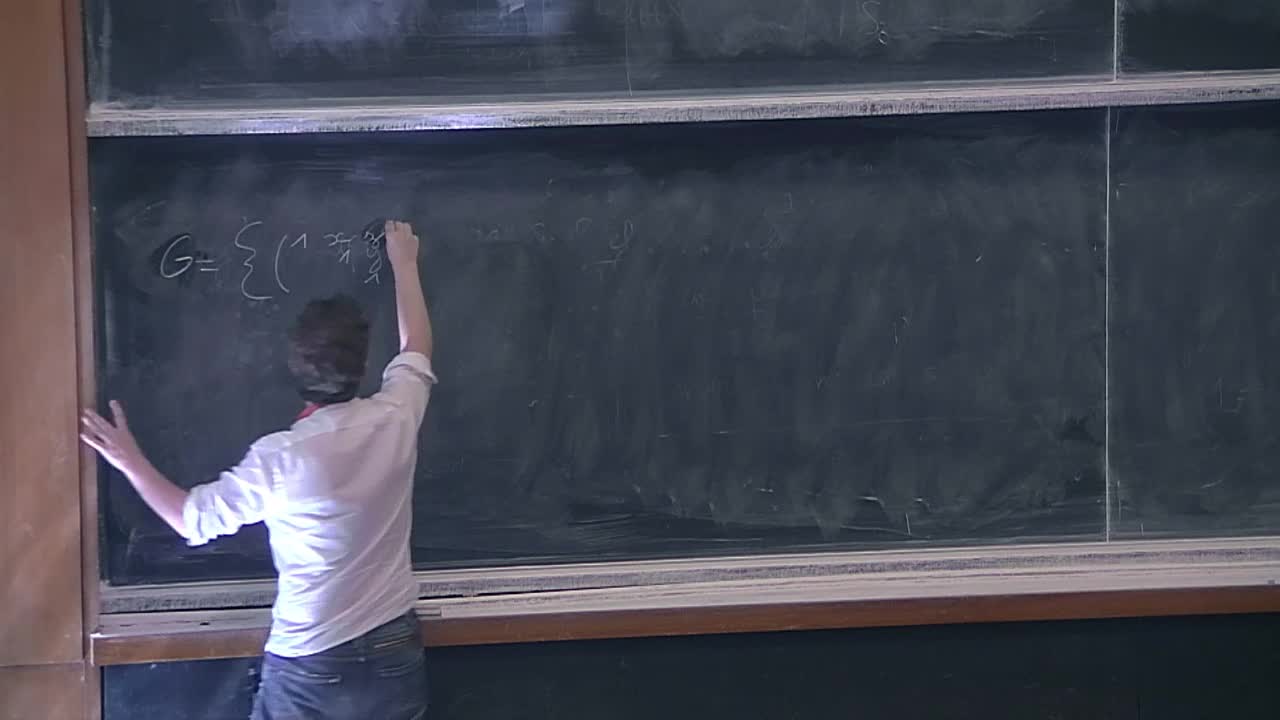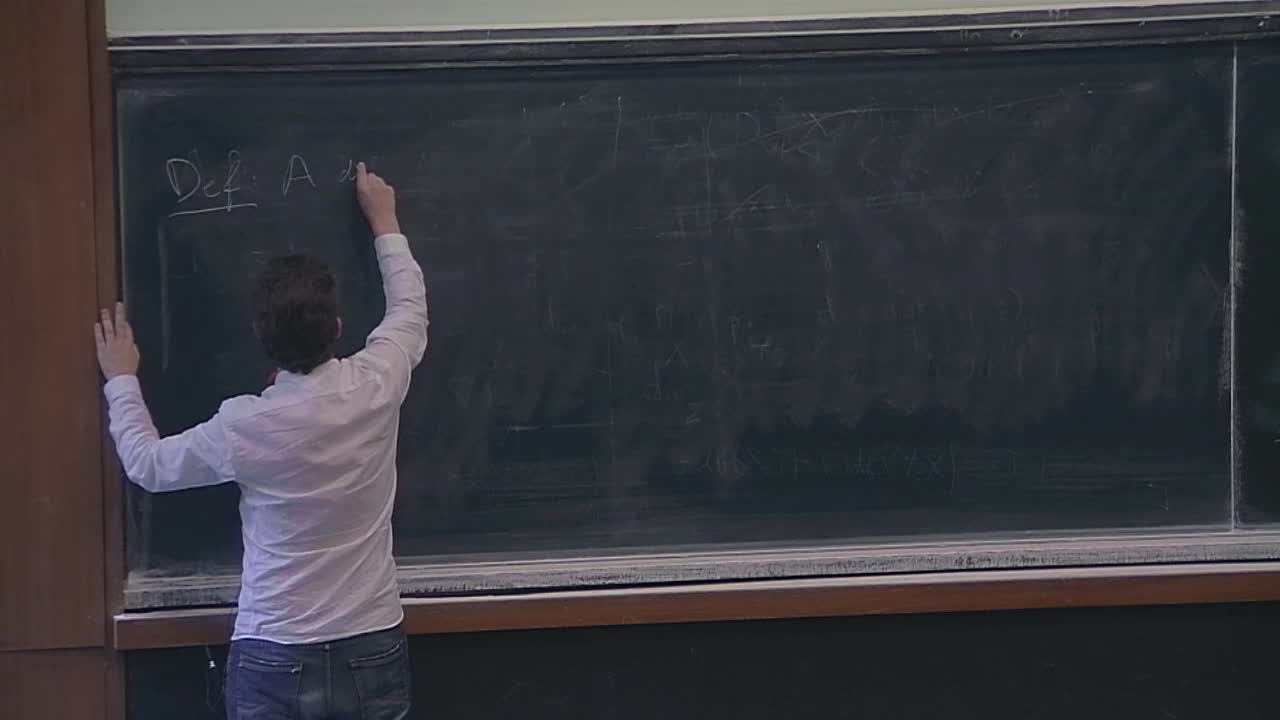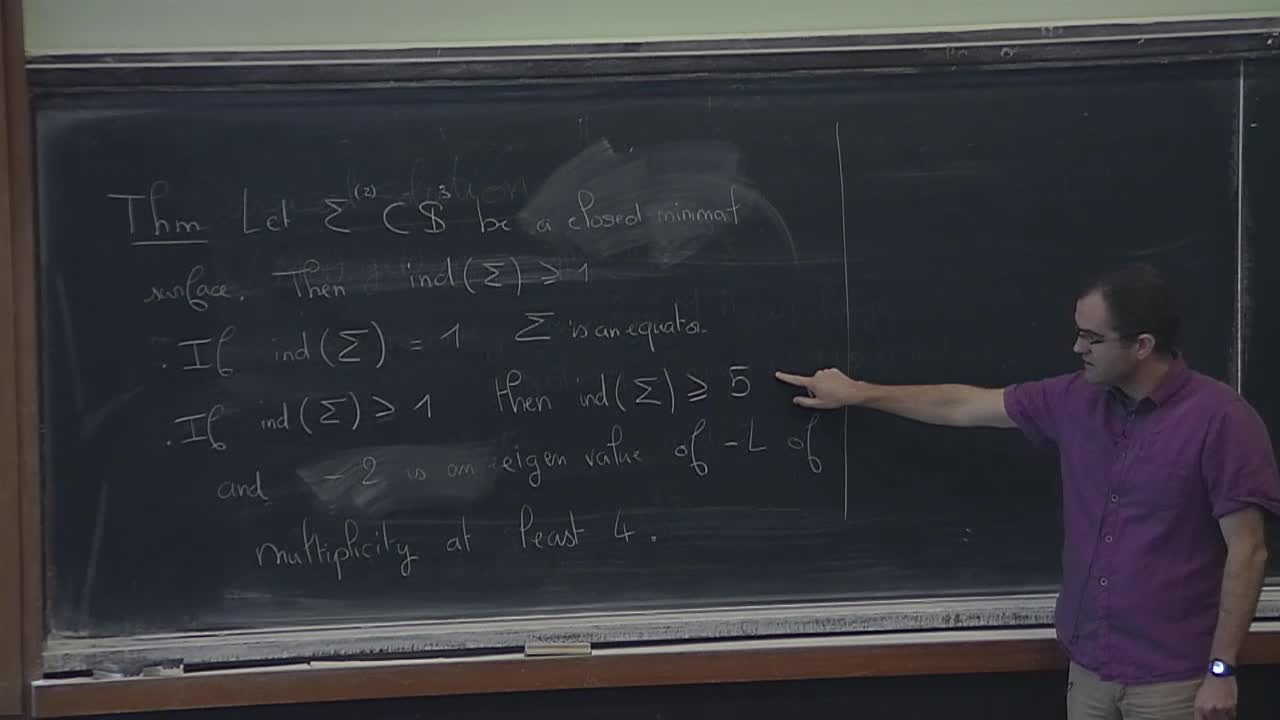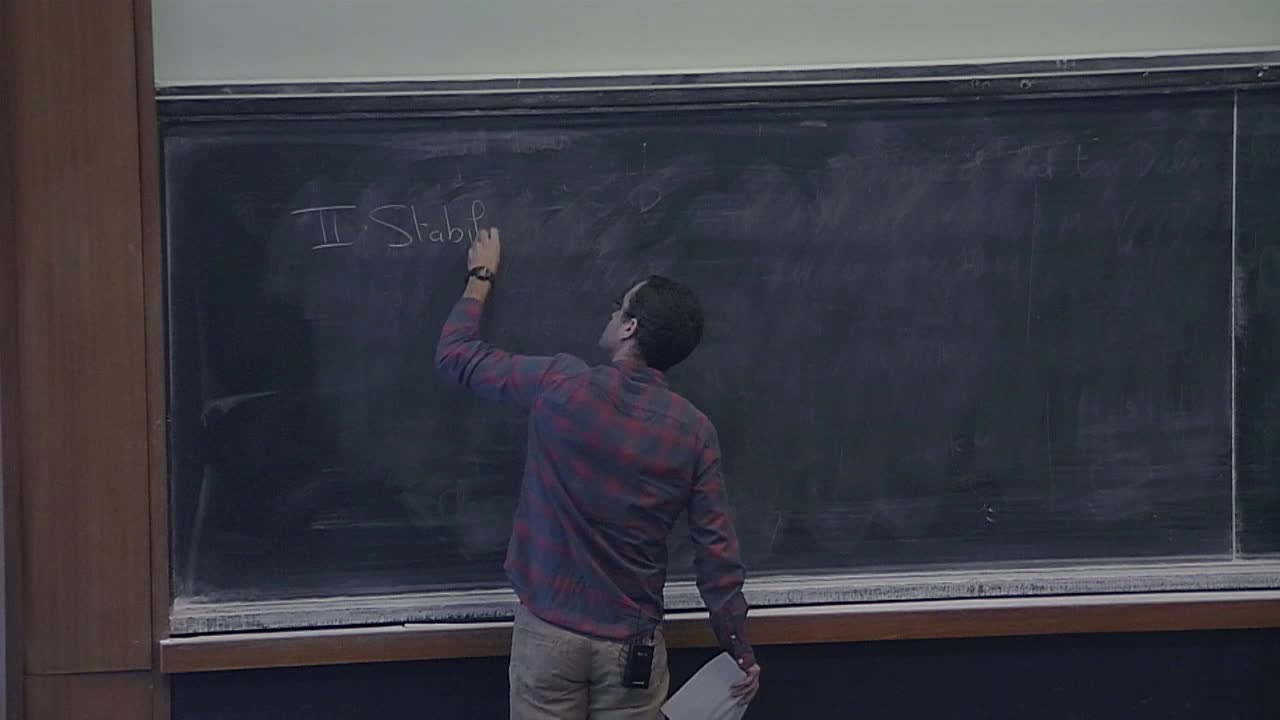2016
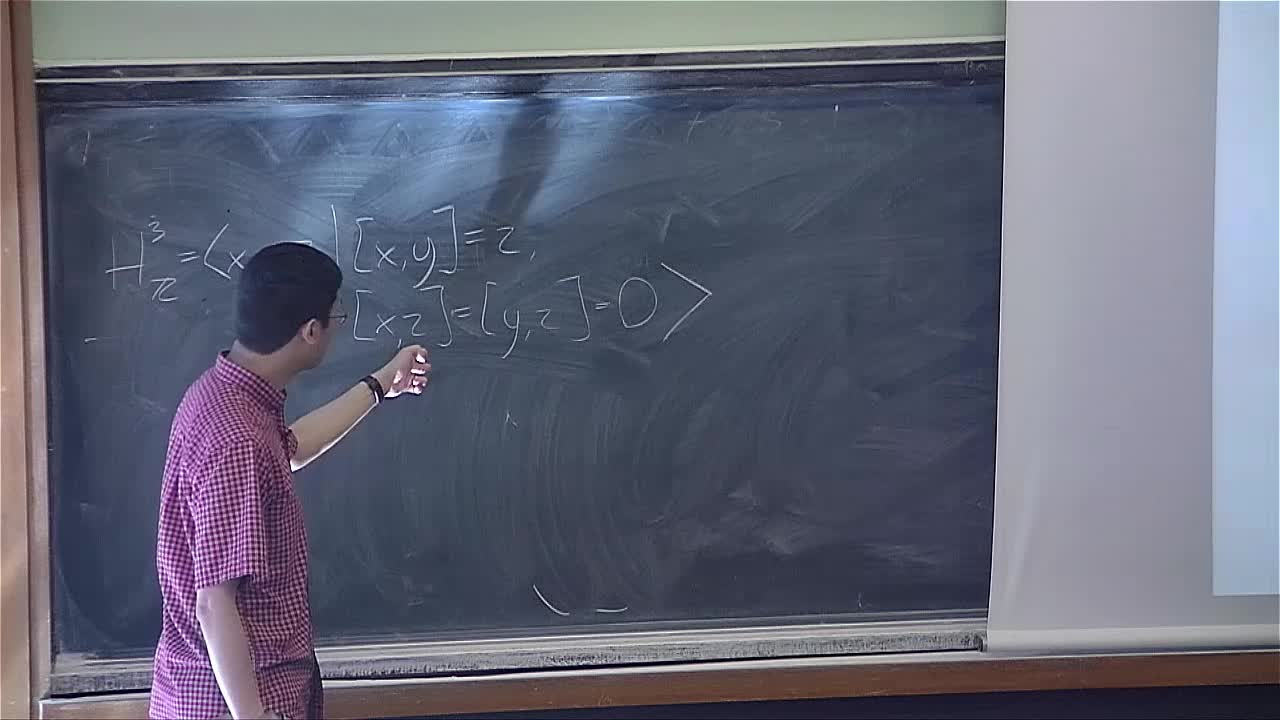
Vidéos
Robert Young - Quantitative geometry and filling problems (Part 5)
Plateau's problem asks whether there exists a minimal surface with a given boundary in Euclidean space. In this course, we will study related problems in broader classes of spaces and ask what the
Robert Young - Quantitative geometry and filling problems (Part 4)
Plateau's problem asks whether there exists a minimal surface with a given boundary in Euclidean space. In this course, we will study related problems in broader classes of spaces and ask what the
Robert Young - Quantitative geometry and filling problems (Part 3)
Plateau's problem asks whether there exists a minimal surface with a given boundary in Euclidean space. In this course, we will study related problems in broader classes of spaces and ask what the
Robert Young - Quantitative geometry and filling problems (Part 2)
Plateau's problem asks whether there exists a minimal surface with a given boundary in Euclidean space. In this course, we will study related problems in broader classes of spaces and ask what the
Robert Young - Quantitative geometry and filling problems (Part 1)
Plateau's problem asks whether there exists a minimal surface with a given boundary in Euclidean space. In this course, we will study related problems in broader classes of spaces and ask what the
Sylvain Maillot - An introduction to open 3-manifolds (Part 4)
W. Thurston's geometrization program has lead to manyoutstanding results in 3-manifold theory. Thanks to worksof G. Perelman, J. Kahn and V. Markovic, D. Wise, and I. Agol among others, compact 3
Sylvain Maillot - An introduction to open 3-manifolds (Part 3)
W. Thurston's geometrization program has lead to manyoutstanding results in 3-manifold theory. Thanks to worksof G. Perelman, J. Kahn and V. Markovic, D. Wise, and I. Agol among others, compact 3
Sylvain Maillot - An introduction to open 3-manifolds (Part 1)
W. Thurston's geometrization program has lead to manyoutstanding results in 3-manifold theory. Thanks to worksof G. Perelman, J. Kahn and V. Markovic, D. Wise, and I. Agol among others, compact 3
Sylvain Maillot - An introduction to open 3-manifolds (Part 2)
W. Thurston's geometrization program has lead to manyoutstanding results in 3-manifold theory. Thanks to worksof G. Perelman, J. Kahn and V. Markovic, D. Wise, and I. Agol among others, compact 3
Feng Luo - An introduction to discrete conformal geometry of polyhedral surfaces (Part 5)
The goal of the course is to introduce some of the recent developments on discrete conformal geometry of polyhedral surfaces. We plan to cover the following topics. - The Andreev-Koebe-Thurston
Feng Luo - An introduction to discrete conformal geometry of polyhedral surfaces (Part 4)
The goal of the course is to introduce some of the recent developments on discrete conformal geometry of polyhedral surfaces. We plan to cover the following topics. - The Andreev-Koebe-Thurston
Feng Luo - An introduction to discrete conformal geometry of polyhedral surfaces (Part 3)
The goal of the course is to introduce some of the recent developments on discrete conformal geometry of polyhedral surfaces. We plan to cover the following topics. - The Andreev-Koebe-Thurston
Feng Luo - An introduction to discrete conformal geometry of polyhedral surfaces (Part 2)
The goal of the course is to introduce some of the recent developments on discrete conformal geometry of polyhedral surfaces. We plan to cover the following topics. - The Andreev-Koebe-Thurston
Feng Luo - An introduction to discrete conformal geometry of polyhedral surfaces (Part 1)
The goal of the course is to introduce some of the recent developments on discrete conformal geometry of polyhedral surfaces. We plan to cover the following topics. - The Andreev-Koebe-Thurston
Gilles Courtois - The Margulis lemma, old and new (Part 5)
The Margulis lemma describes the structure of the group generated by small loops in the fundamental group of a Riemannian manifold, thus giving a picture of its local topology. Originally stated for
Gilles Courtois - The Margulis lemma, old and new (Part 4)
The Margulis lemma describes the structure of the group generated by small loops in the fundamental group of a Riemannian manifold, thus giving a picture of its local topology. Originally stated for
Gilles Courtois - The Margulis lemma, old and new (Part 3)
The Margulis lemma describes the structure of the group generated by small loops in the fundamental group of a Riemannian manifold, thus giving a picture of its local topology. Originally stated for
Gilles Courtois - The Margulis lemma, old and new (Part 2)
The Margulis lemma describes the structure of the group generated by small loops in the fundamental group of a Riemannian manifold, thus giving a picture of its local topology. Originally stated for
Gilles Courtois - The Margulis lemma, old and new (Part 1)
The Margulis lemma describes the structure of the group generated by small loops in the fundamental group of a Riemannian manifold, thus giving a picture of its local topology. Originally stated for
Greg McShane - Volumes of hyperbolics manifolds and translation distances
Schlenker and Krasnov have established a remarkable Schlaffli-type formula for the (renormalized) volume of a quasi-Fuchsian manifold. Using this, some classical results in complex analysis and Gromov
Laurent Mazet - Minimal hypersurfaces of least area
In this talk, I will present a joint work with H. Rosenberg where we give a characterization of the minimal hypersurface of least area in any Riemannian manifold. As a consequence, we give a lower
Daniel Ketover - Sharp entropy bounds of closed surfaces and min-max theory
In 2012, Colding-Ilmanen-Minicozzi-White conjectured that the entropy of any closed surface in R^3 is at least that of the self-shrinking two-sphere. I will explain joint work with X. Zhou where we
Electrical Networks and Stephenson's Conjecture
The Riemann Mapping Theorem asserts that any simply connected planar domain which is not the whole of it, can be mapped by a conformal homeomorphism onto the open unit disk. After normalization, this
David Gabai - Maximal cusps of low volume
With Robert Haraway, Robert Meyerhoff, Nathaniel Thurston and Andrew Yarmola. We address the following question. What are all the 1-cusped hyperbolic 3-manifolds whose maximal cusps have low volume?
Reto Buzano - Minimal hypersurfaces with bounded index and bounded area
We study sequences of closed minimal hypersurfaces (in closed Riemannian manifolds) that have uniformly bounded index and area. In particular, we develop a bubbling result which yields a bound on the
Robert Young - Quantitative rectifiability and differentiation in the Heisenberg group
(joint work with Assaf Naor) The Heisenberg group $\mathbb{H}$ is a sub-Riemannian manifold that is unusually difficult to embed in $\mathbb{R}^n$. Cheeger and Kleiner introduced a new notion of
Burkhard Wilking - Manifolds with almost nonnegative curvature operator
Manifolds with almost nonnegative curvature operator
Genevieve Walsh - Boundaries of Kleinian groups
We study the problem of classifying Kleinian groups via the topology of their limit sets. In particular, we are interested in one-ended convex-cocompact Kleinian groups where each piece in the JSJ
Jeff Viaclovsky - Deformation theory of scalar-flat Kahler ALE surfaces
I will discuss a Kuranishi-type theorem for deformations of complex structure on ALE Kahler surfaces, which will be used to prove that for any scalar-flat Kahler ALE surface, all small deformations of
Juan Souto - Counting curves on surfaces
An old theorem of Huber asserts that the number of closed geodesics of length at most L on a hyperbolic surface is asymptotic to $\frac{e^L}L$. However, things are less clear if one either fixes the
Jean-Marc Schlenker - Anti-de Sitter geometry and polyhedra inscribed in quadrics
Anti-de Sitter geometry is a Lorentzian analog of hyperbolic geometry. In the last 25 years a number of connections have emerged between 3-dimensional anti-de Sitter geometry and the geometry of
Stéphane Saboureau - Sweep-outs, width estimates and volume
Sweep-out techniques in geometry and topology have recently received a great deal of attention, leading to major breakthroughs. In this talk, we will present several width estimates relying on min-max
Melanie Rupflin - Horizontal curves of metrics and applications to geometric flows
On closed surfaces there are three basic ways to evolve a metric, by conformal change, by pull-back with diffeomorphisms and by horizontal curves, moving orthogonally to the first two types of
Vladimir Markovic - Harmonic quasi-isometries between negatively curved manifolds
Very recently, Markovic, Lemm-Markovic and Benoist-Hulin, established the existence of a harmonic mapping in the homotopy class of an arbitrary quasi-isometry between rank 1 symmetric spaces. I will
Feng Luo - Discrete conformal geometry of polyhedral surfaces and its convergence
Our recent joint work with D. Gu established a discrete version of the uniformization theorem for compact polyhedral surfaces. In this talk, we prove that discrete uniformizaton maps converge to
Robert Haslhofer - The moduli space of 2-convex embedded spheres
We investigate the topology of the space of smoothly embedded n-spheres in R^{n+1}, i.e. the quotient space M_n:=Emb(S^n,R^{n+1})/Diff(S^n). By Hatcher’s proof of the Smale conjecture, M_2 is
Igor Belegradek - Smoothness of Minkowski sum and generic rotations
I will discuss whether the Minkowski sum of two compact convex bodies can be made smoother by a generic rotation of one of them. Here "generic" is understood in the sense of Baire category. The main
Vincent Beffara - Percolation of random nodal lines
Percolation of random nodal lines
Thomas Richard - Lower bounds on Ricci curvature, with a glimpse on limit spaces (Part 5)
The goal of these lectures is to introduce some fundamental tools in the study of manifolds with a lower bound on Ricci curvature. We will first state and prove the laplacian comparison theorem
Thomas Richard - Lower bounds on Ricci curvature, with a glimpse on limit spaces (Part 4)
The goal of these lectures is to introduce some fundamental tools in the study of manifolds with a lower bound on Ricci curvature. We will first state and prove the laplacian comparison theorem
Thomas Richard - Lower bounds on Ricci curvature, with a glimpse on limit spaces (Part 3)
The goal of these lectures is to introduce some fundamental tools in the study of manifolds with a lower bound on Ricci curvature. We will first state and prove the laplacian comparison theorem
Thomas Richard - Lower bounds on Ricci curvature, with a glimpse on limit spaces (Part 2)
The goal of these lectures is to introduce some fundamental tools in the study of manifolds with a lower bound on Ricci curvature. We will first state and prove the laplacian comparison theorem
Thomas Richard - Lower bounds on Ricci curvature, with a glimpse on limit spaces (Part 1)
The goal of these lectures is to introduce some fundamental tools in the study of manifolds with a lower bound on Ricci curvature. We will first state and prove the laplacian comparison theorem
Laurent Mazet - Some aspects of minimal surface theory (Part 5)
In a Riemannian 3-manifold, minimal surfaces are critical points of the area functional and can be a useful tool to understand the geometry and the topology of the ambient manifold. The aim of
Laurent Mazet - Some aspects of minimal surface theory (Part 4)
In a Riemannian 3-manifold, minimal surfaces are critical points of the area functional and can be a useful tool to understand the geometry and the topology of the ambient manifold. The aim of
Laurent Mazet - Some aspects of minimal surface theory (Part 3)
In a Riemannian 3-manifold, minimal surfaces are critical points of the area functional and can be a useful tool to understand the geometry and the topology of the ambient manifold. The aim of
Laurent Mazet - Some aspects of minimal surface theory (Part 2)
In a Riemannian 3-manifold, minimal surfaces are critical points of the area functional and can be a useful tool to understand the geometry and the topology of the ambient manifold. The aim of
Laurent Mazet - Some aspects of minimal surface theory (Part 1)
In a Riemannian 3-manifold, minimal surfaces are critical points of the area functional and can be a useful tool to understand the geometry and the topology of the ambient manifold. The aim of
Intervenants et intervenantes
Auteur d'une thèse de : Mathématiques, Université Paris-Sud 11, Orsay (en 2003)
Directeur de recherche CNRS à l'Institut Fourier (depuis 2015-09-01)
Professeur à l'école de mathématiques du Georgia Tech College of Science (2016)
Professeur associé de géométrie à l'Università degli Studi di Torino (UniTo) (2016)
Mathématicien. Directeur de recherche CNRS, membre de l'équipe de recherche Analyse complexe et géométrie, Institut de mathématiques de Jussieu - Paris Rive gauche (IMJ-PRG, UMR 7586), Sorbonne université et Université de Paris (en 2021)
Docteur en mathématiques (Grenoble 1, 1987)
Membre du jury d'une thèse en Mathématiques à Université Côte d'Azur en 2025
Mathématicien. En poste à l'université Princeton, N.J. (en 2011)
Professeur et chercheur au département de mathématiques de l'université de Géorgie (en 2016)
Enseigne l'analyse géométrique à la Princeton University working in geometric analysis (2016)
Titulaire d'un doctorat en mathématiques (Université de Californie, San Diego, 1989) Mathématicien. En poste à l'Université Rutgers à New Brunswick, NJ, depuis 1993.
Titulaire d'une thèse de doctorat en mathématiques pures soutenue à l'Université Paul Sabatier à Toulouse (en 2000)
Mathématicien. Enseigne à l'Institut de Mathématiques et de Modélisation, Université de Montpellier II (en 2010)
Mathématicien. Chargé de Recherche CNRS affecté au Laboratoire d’Analyse et Mathématiques Appliquées (UPEC) (de 2007 à 2018). Professeur à l'Université de Tours et membre de l'Institut Denis Poisson, spécialité : géométrie riemannienne et analyse géométrique (depuis 2018-09)
Titulaire d'une thèse de doctorat en mathématiques pures, Université Paul Sabatier, Toulouse (en 2004)
Auteur d'une thèse en mathématiques à Grenoble en 2012
Mathématicienne. Professeure au Mathematical Institute de l'Université d'Oxford (2016)
Auteur d'une thèse de mathématiques soutenue à Montpellier le 14 décembre 2001
Mathématicien. Maître de conférence à l'Université de Tours et membre du Laboratoire de Mathématiques et Physique Théorique (LMPT, UMR 7050) et de la Fédération Denis Poisson (jusqu'en 2011-07). Professeur des universités, membre de l'équipe de recherche Géométrie et courbure, Laboratoire analyse et mathématiques appliquées (LAMA, UMR 8050), Université Paris-Est Créteil Val-de-Marne (depuis 2011-08)
Elève-ingénieur de l'Ecole polytechnique, promotion 1988. Professeur de mathématiques à l'université Paul Sabatier à Toulouse (en 2005)
Professeur de mathématiques, Université du Luxembourg (depuis 2013)
Professeur au Département de Mathématiques de l'Université de Californie (2016)
Professeur de l'institut de mathématiques de l'Université de Münster (2016)