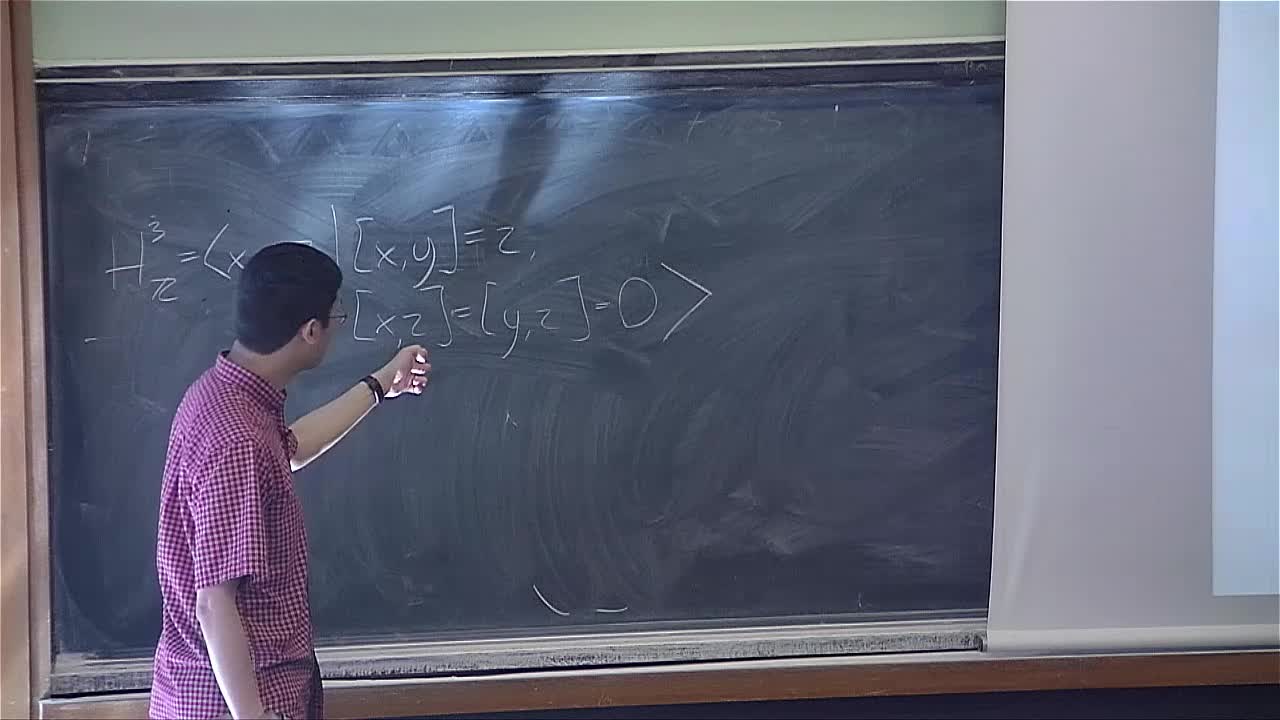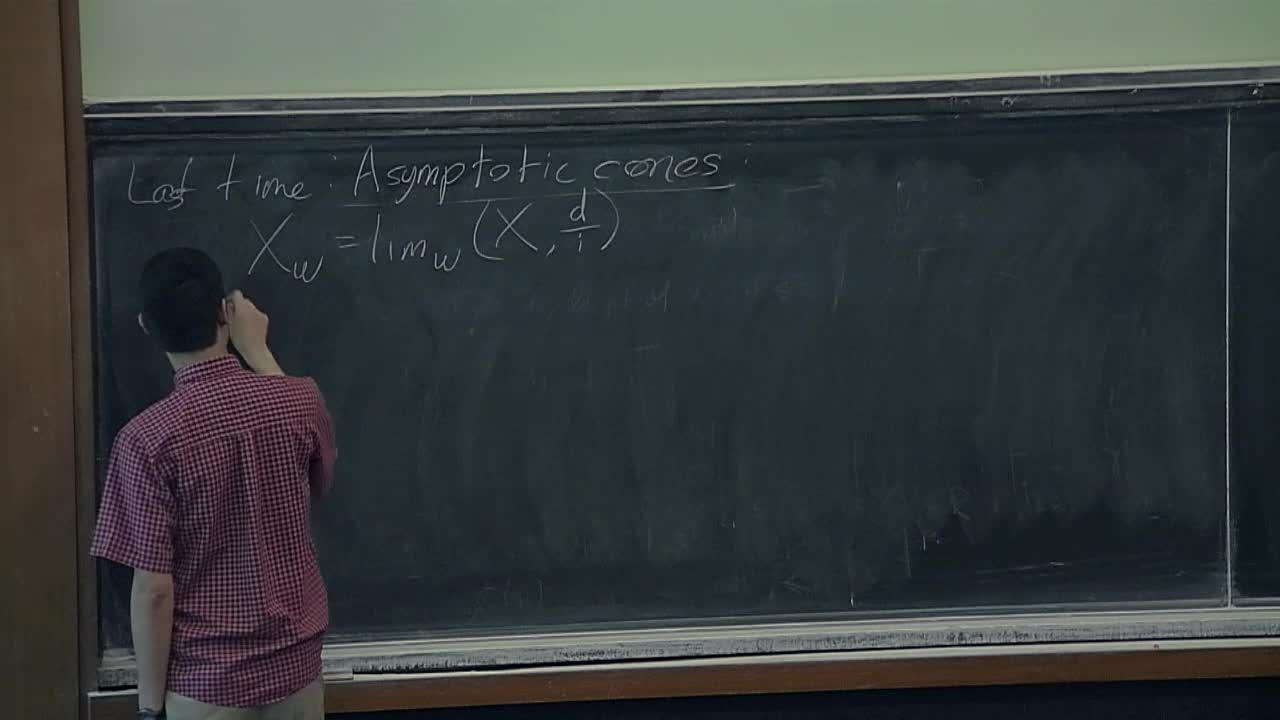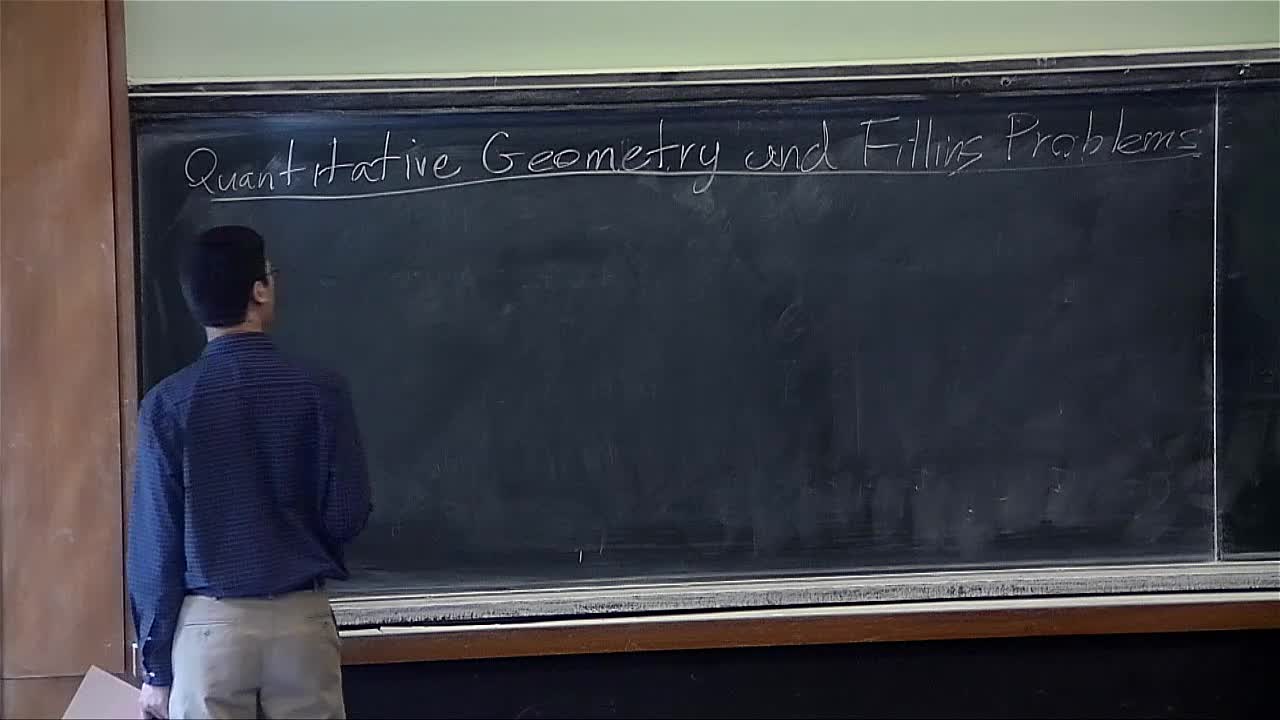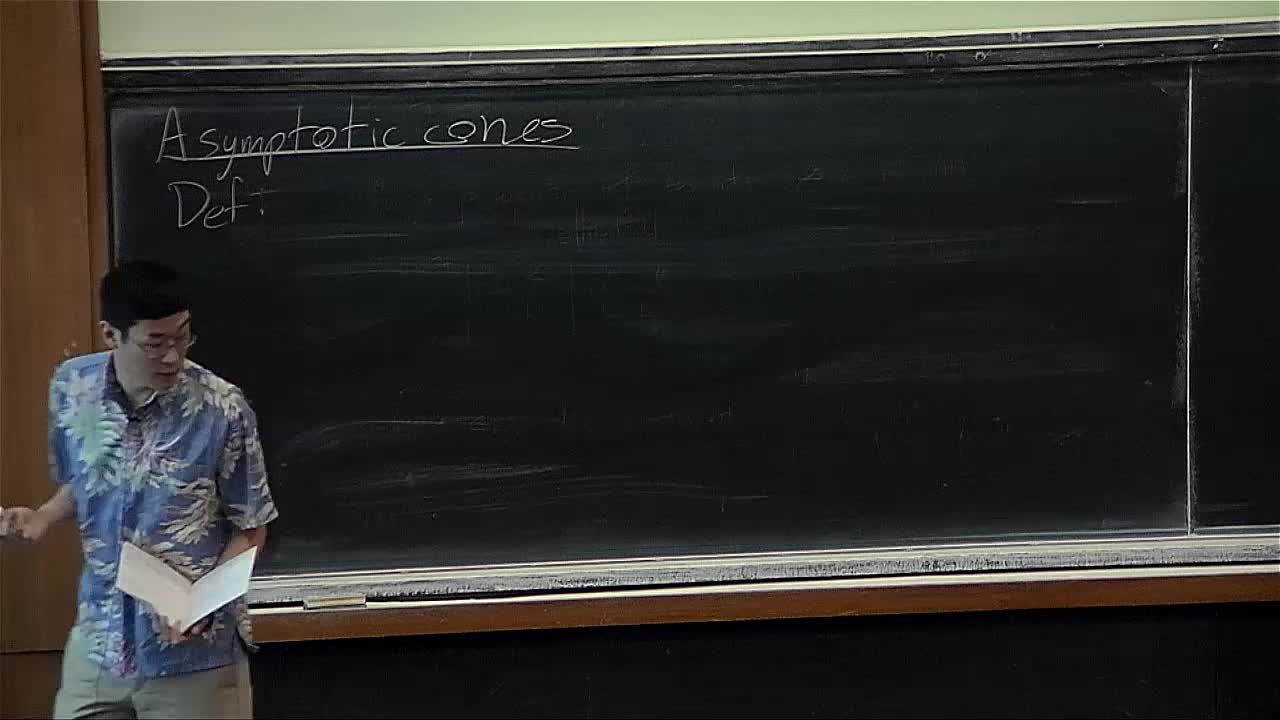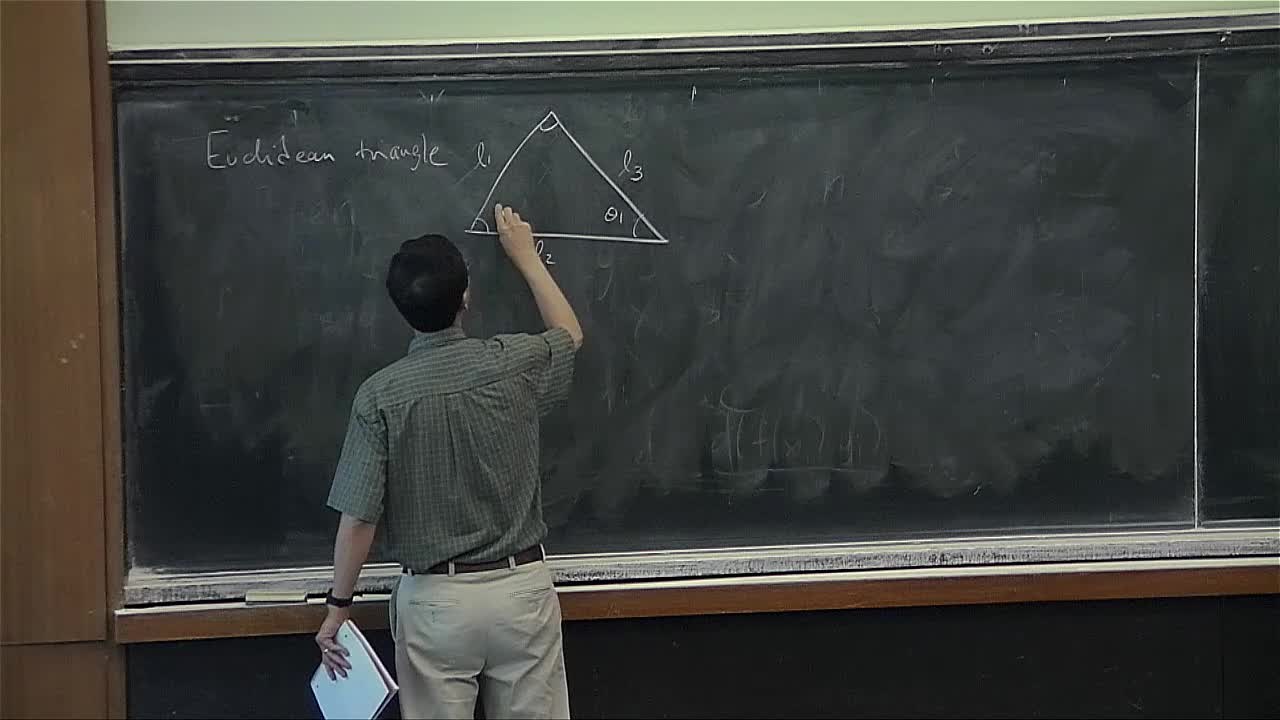Notice
Sylvain Maillot - An introduction to open 3-manifolds (Part 4)
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
W. Thurston's geometrization program has lead to manyoutstanding results in 3-manifold theory. Thanks to worksof G. Perelman, J. Kahn and V. Markovic, D. Wise, and I. Agol among others, compact 3-manifolds can now beconsidered to be reasonably well-understood.By contrast, noncompact 3-manifolds remainmuch more mysterious. There is a series of examples,beginning with work of L. Antoine and J. H. C. Whitehead,which show that open 3-manifolds can exhibit wildbehavior at infinity. No comprehensive structure theoryanalogous to geometrization à la Thurston is currently availablefor these objects
In these lectures, we will focus on two aspects of the subject:
(1) constructing interesting examples, and
(2) finding sufficientconditions that rule out exotic examples, in particular inconnection with Riemannian geometry.
Dans la même collection
-
Robert Young - Quantitative geometry and filling problems (Part 5)
Plateau's problem asks whether there exists a minimal surface with a given boundary in Euclidean space. In this course, we will study related problems in broader classes of spaces and ask what the
-
Robert Young - Quantitative geometry and filling problems (Part 2)
Plateau's problem asks whether there exists a minimal surface with a given boundary in Euclidean space. In this course, we will study related problems in broader classes of spaces and ask what the
-
Robert Young - Quantitative geometry and filling problems (Part 4)
Plateau's problem asks whether there exists a minimal surface with a given boundary in Euclidean space. In this course, we will study related problems in broader classes of spaces and ask what the
-
Robert Young - Quantitative geometry and filling problems (Part 1)
Plateau's problem asks whether there exists a minimal surface with a given boundary in Euclidean space. In this course, we will study related problems in broader classes of spaces and ask what the
-
Robert Young - Quantitative geometry and filling problems (Part 3)
Plateau's problem asks whether there exists a minimal surface with a given boundary in Euclidean space. In this course, we will study related problems in broader classes of spaces and ask what the
-
Sylvain Maillot - An introduction to open 3-manifolds (Part 3)
MAILLOT Sylvain
W. Thurston's geometrization program has lead to manyoutstanding results in 3-manifold theory. Thanks to worksof G. Perelman, J. Kahn and V. Markovic, D. Wise, and I. Agol among others, compact 3
-
Feng Luo - An introduction to discrete conformal geometry of polyhedral surfaces (Part 5)
LUO Feng
The goal of the course is to introduce some of the recent developments on discrete conformal geometry of polyhedral surfaces. We plan to cover the following topics. - The Andreev-Koebe-Thurston
-
Feng Luo - An introduction to discrete conformal geometry of polyhedral surfaces (Part 2)
LUO Feng
The goal of the course is to introduce some of the recent developments on discrete conformal geometry of polyhedral surfaces. We plan to cover the following topics. - The Andreev-Koebe-Thurston
-
Sylvain Maillot - An introduction to open 3-manifolds (Part 1)
MAILLOT Sylvain
W. Thurston's geometrization program has lead to manyoutstanding results in 3-manifold theory. Thanks to worksof G. Perelman, J. Kahn and V. Markovic, D. Wise, and I. Agol among others, compact 3
-
Feng Luo - An introduction to discrete conformal geometry of polyhedral surfaces (Part 4)
LUO Feng
The goal of the course is to introduce some of the recent developments on discrete conformal geometry of polyhedral surfaces. We plan to cover the following topics. - The Andreev-Koebe-Thurston
-
Feng Luo - An introduction to discrete conformal geometry of polyhedral surfaces (Part 1)
LUO Feng
The goal of the course is to introduce some of the recent developments on discrete conformal geometry of polyhedral surfaces. We plan to cover the following topics. - The Andreev-Koebe-Thurston
-
Sylvain Maillot - An introduction to open 3-manifolds (Part 2)
MAILLOT Sylvain
W. Thurston's geometrization program has lead to manyoutstanding results in 3-manifold theory. Thanks to worksof G. Perelman, J. Kahn and V. Markovic, D. Wise, and I. Agol among others, compact 3
Avec les mêmes intervenants et intervenantes
-
Sylvain Maillot - An introduction to open 3-manifolds (Part 2)
MAILLOT Sylvain
W. Thurston's geometrization program has lead to manyoutstanding results in 3-manifold theory. Thanks to worksof G. Perelman, J. Kahn and V. Markovic, D. Wise, and I. Agol among others, compact 3
-
Sylvain Maillot - An introduction to open 3-manifolds (Part 1)
MAILLOT Sylvain
W. Thurston's geometrization program has lead to manyoutstanding results in 3-manifold theory. Thanks to worksof G. Perelman, J. Kahn and V. Markovic, D. Wise, and I. Agol among others, compact 3
-
Sylvain Maillot - An introduction to open 3-manifolds (Part 3)
MAILLOT Sylvain
W. Thurston's geometrization program has lead to manyoutstanding results in 3-manifold theory. Thanks to worksof G. Perelman, J. Kahn and V. Markovic, D. Wise, and I. Agol among others, compact 3
Sur le même thème
-
"Le mathématicien Petre (Pierre) Sergescu, historien des sciences, personnalité du XXe siècle"
HERLéA Alexandre
Alexandre HERLEA est membre de la section « Sciences, histoire des sciences et des techniques et archéologie industrielle » du CTHS. Professeur émérite des universités, membre effectif de l'Académie
-
Webinaire sur la rédaction des PGD
LOUVET Violaine
Rédaction des Plans de Gestion de Données (PGD) sous l’angle des besoins de la communauté mathématique.
-
Alexandre Booms : « Usage de matériel pédagogique adapté en géométrie : une transposition à interro…
« Usage de matériel pédagogique adapté en géométrie : une transposition à interroger ». Alexandre Booms, doctorant (Université de Reims Champagne-Ardenne - Cérep UR 4692)
-
A. Mondino - Time-like Ricci curvature bounds via optimal transport
MONDINO Andrea
The goal of the talk is to present a recent work in collaboration with Cavalletti (SISSA) on optimal transport in Lorentzian synthetic spaces. The aim is to set up a “Lorentzian analog” of the
-
M. Lesourd - Positive Scalar Curvature on Noncompact Manifolds and the Positive Mass Theorem
LESOURD Martin
The study of positive scalar curvature on noncompact manifolds has seen significant progress in the last few years. A major role has been played by Gromov's results and conjectures, and in
-
J. Wang - Topological rigidity and positive scalar curvature
WANG Jian
In this talk, we shall describe some topological rigidity and its relationship with positive scalar curvature. Precisely, we will present a proof that a complete contractible 3-manifold with
-
R. Perales - Recent Intrinsic Flat Convergence Theorems
PERALES Raquel
Théorèmes récents de convergence plane intrinsèque
-
J. Fine - Knots, minimal surfaces and J-holomorphic curves
FINE Joël
I will describe work in progress, parts of which are joint with Marcelo Alves. Let L be a knot or link in the 3-sphere. I will explain how one can count minimal surfaces in hyperbolic 4-space
-
D. Semola - Boundary regularity and stability under lower Ricci bounds
SEMOLA Daniele
The theory of non smooth spaces with lower Ricci Curvature bounds has undergone huge developments in the last thirty years. On the one hand the impetus came from Gromov’s precompactness theorem
-
D. Stern - Harmonic map methods in spectral geometry
STERN Daniel
Over the last fifty years, the problem of finding sharp upper bounds for area-normalized Laplacian eigenvalues on closed surfaces has attracted the attention of many geometers, due in part to
-
P. Burkhardt - Pointwise lower scalar curvature bounds for C0 metrics via regularizing Ricci flow
BURKHARDT-GUIM Paula
We propose a class of local definitions of weak lower scalar curvature bounds that is well defined for C0 metrics. We show the following: that our definitions are stable under greater-than-second
-
R. Bamler - Compactness and partial regularity theory of Ricci flows in higher dimensions
BAMLER Richard H.
We present a new compactness theory of Ricci flows. This theory states that any sequence of Ricci flows that is pointed in an appropriate sense, subsequentially converges to a synthetic flow.