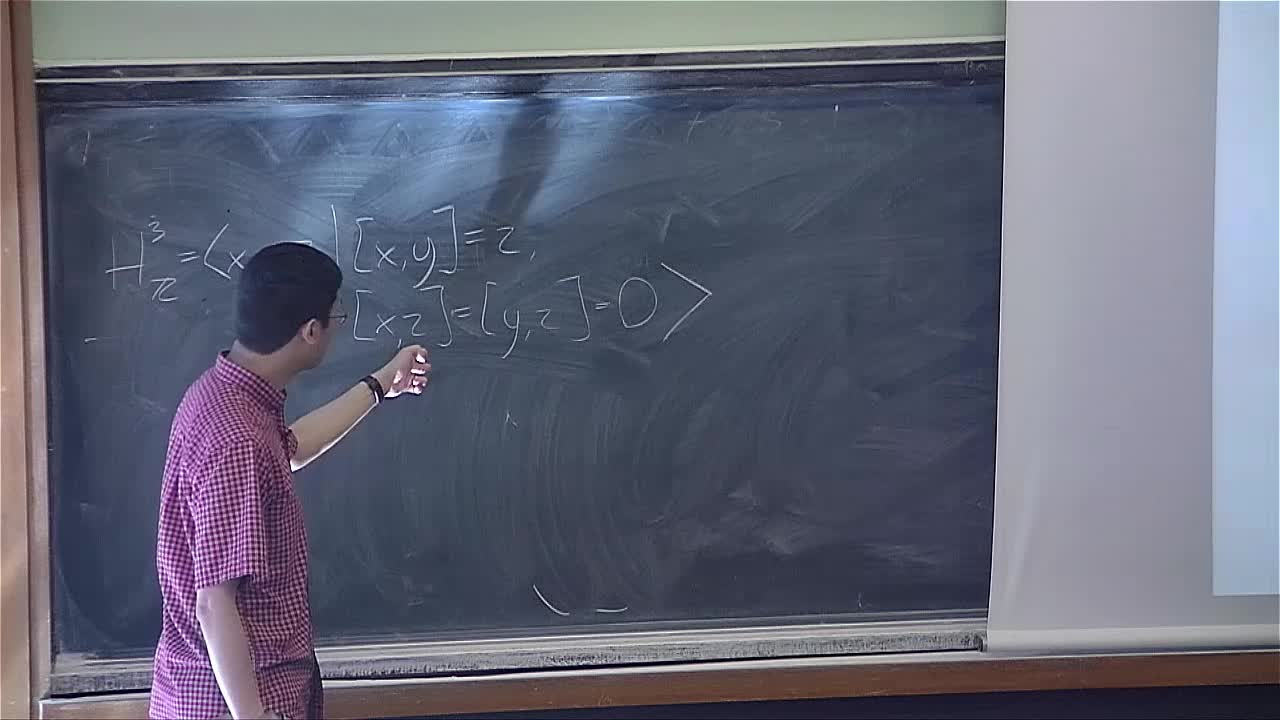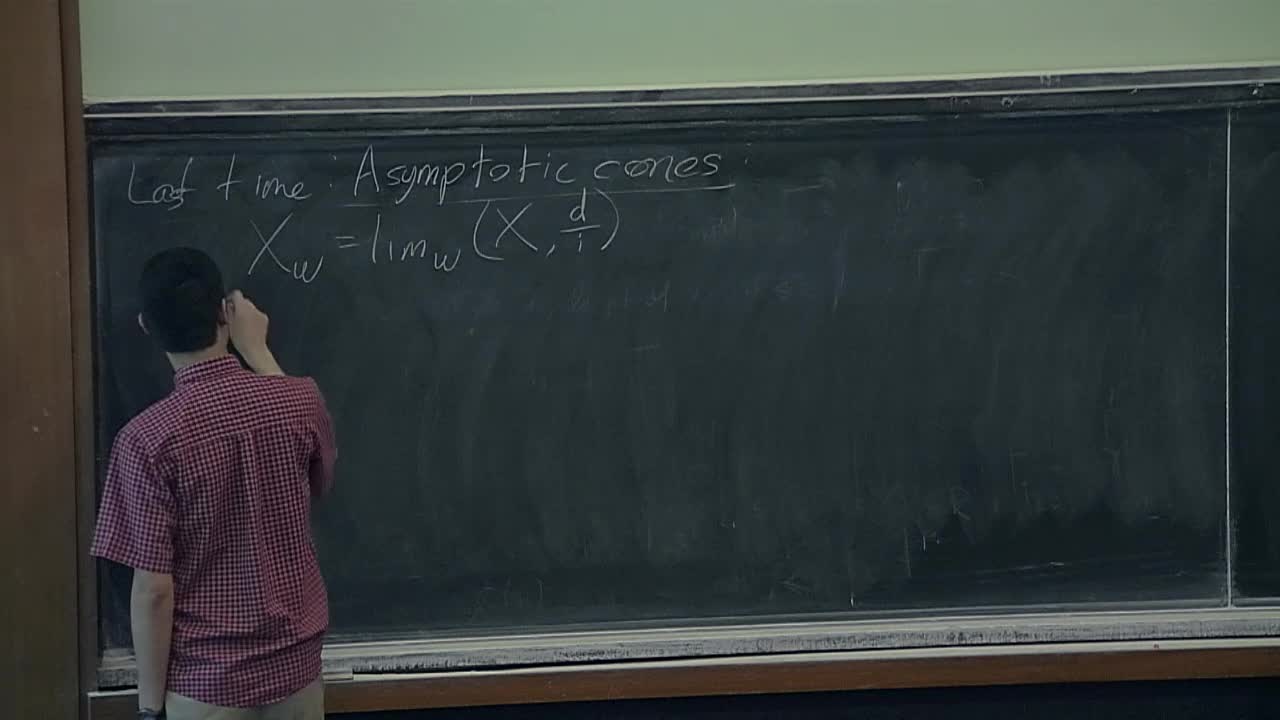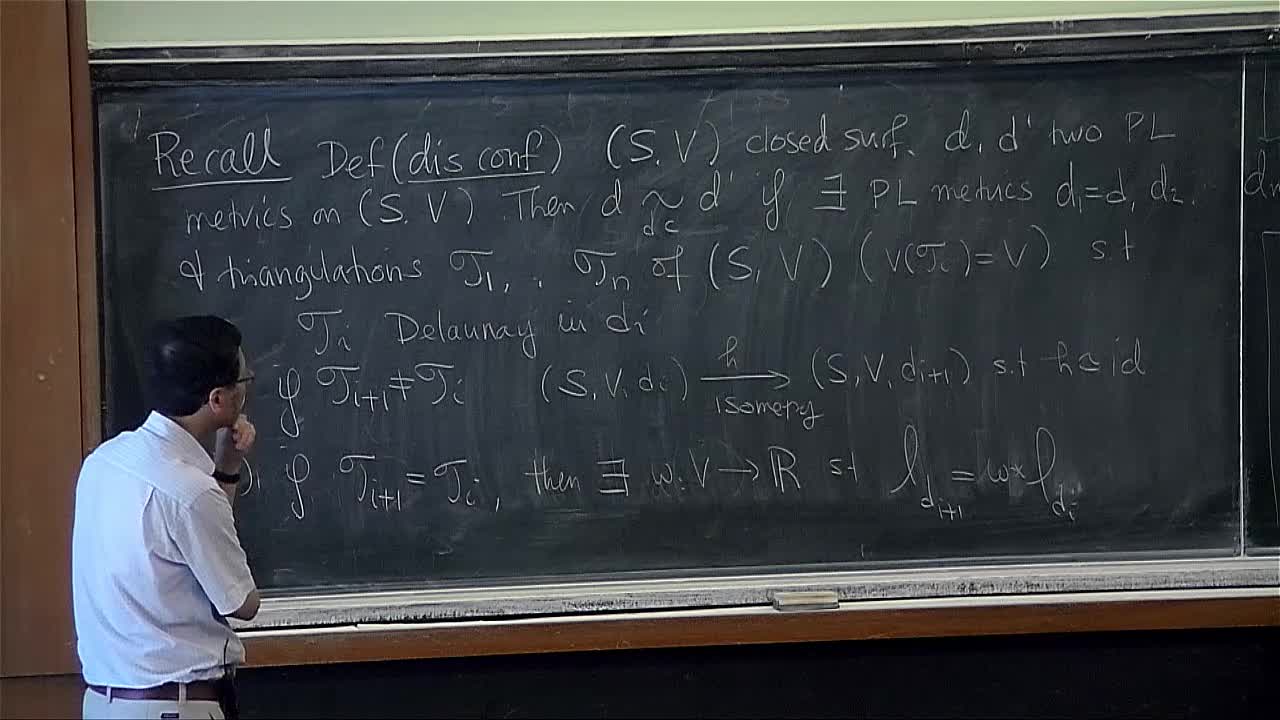Notice
Jeff Viaclovsky - Deformation theory of scalar-flat Kahler ALE surfaces
- document 1 document 2 document 3
- niveau 1 niveau 2 niveau 3
Descriptif
I will discuss a Kuranishi-type theorem for deformations of complex structure on ALE Kahler surfaces, which will be used to prove that for any scalar-flat Kahler ALE surface, all small deformations of complex structure also admit scalar-flat Kahler ALE metrics. A local moduli space of scalar-flat Kahler ALE metrics can then be constructed, which is universal up to small diffeomorphisms. I will also discuss a formula for the dimension of the local moduli space in the case of a scalar-flat Kahler ALE surface which deforms to a minimal resolution of an isolated quotient singularity. This is joint work with Jiyuan Han.
Intervention / Responsable scientifique
Thème
Dans la même collection
-
Robert Young - Quantitative geometry and filling problems (Part 5)
Plateau's problem asks whether there exists a minimal surface with a given boundary in Euclidean space. In this course, we will study related problems in broader classes of spaces and ask what the
-
Robert Young - Quantitative geometry and filling problems (Part 2)
Plateau's problem asks whether there exists a minimal surface with a given boundary in Euclidean space. In this course, we will study related problems in broader classes of spaces and ask what the
-
Robert Young - Quantitative geometry and filling problems (Part 4)
Plateau's problem asks whether there exists a minimal surface with a given boundary in Euclidean space. In this course, we will study related problems in broader classes of spaces and ask what the
-
Robert Young - Quantitative geometry and filling problems (Part 1)
Plateau's problem asks whether there exists a minimal surface with a given boundary in Euclidean space. In this course, we will study related problems in broader classes of spaces and ask what the
-
Robert Young - Quantitative geometry and filling problems (Part 3)
Plateau's problem asks whether there exists a minimal surface with a given boundary in Euclidean space. In this course, we will study related problems in broader classes of spaces and ask what the
-
Sylvain Maillot - An introduction to open 3-manifolds (Part 4)
MaillotSylvainW. Thurston's geometrization program has lead to manyoutstanding results in 3-manifold theory. Thanks to worksof G. Perelman, J. Kahn and V. Markovic, D. Wise, and I. Agol among others, compact 3
-
Feng Luo - An introduction to discrete conformal geometry of polyhedral surfaces (Part 1)
LuoFengThe goal of the course is to introduce some of the recent developments on discrete conformal geometry of polyhedral surfaces. We plan to cover the following topics. - The Andreev-Koebe-Thurston
-
Sylvain Maillot - An introduction to open 3-manifolds (Part 2)
MaillotSylvainW. Thurston's geometrization program has lead to manyoutstanding results in 3-manifold theory. Thanks to worksof G. Perelman, J. Kahn and V. Markovic, D. Wise, and I. Agol among others, compact 3
-
Feng Luo - An introduction to discrete conformal geometry of polyhedral surfaces (Part 3)
LuoFengThe goal of the course is to introduce some of the recent developments on discrete conformal geometry of polyhedral surfaces. We plan to cover the following topics. - The Andreev-Koebe-Thurston
-
Sylvain Maillot - An introduction to open 3-manifolds (Part 3)
MaillotSylvainW. Thurston's geometrization program has lead to manyoutstanding results in 3-manifold theory. Thanks to worksof G. Perelman, J. Kahn and V. Markovic, D. Wise, and I. Agol among others, compact 3
-
Feng Luo - An introduction to discrete conformal geometry of polyhedral surfaces (Part 5)
LuoFengThe goal of the course is to introduce some of the recent developments on discrete conformal geometry of polyhedral surfaces. We plan to cover the following topics. - The Andreev-Koebe-Thurston
-
Feng Luo - An introduction to discrete conformal geometry of polyhedral surfaces (Part 2)
LuoFengThe goal of the course is to introduce some of the recent developments on discrete conformal geometry of polyhedral surfaces. We plan to cover the following topics. - The Andreev-Koebe-Thurston
Sur le même thème
-
Tuan Ta Pesao : écritures de sable et de ficelle à l'Ile d'Ambrym
VandendriesscheEricCe film se déroule au Nord de l’île d’Ambrym, dans l’archipel de Vanuatu, en Mélanésie...
-
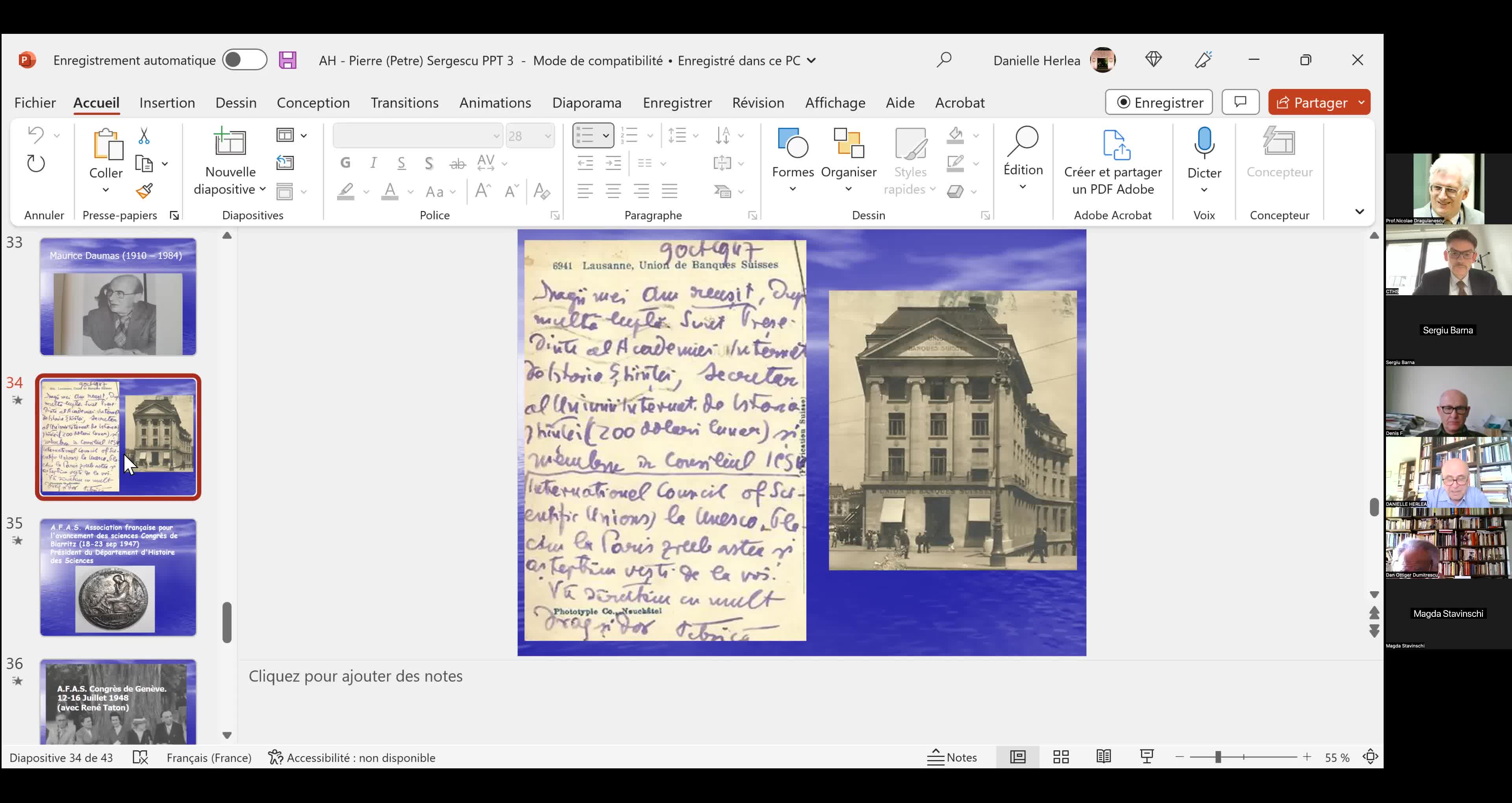
"Le mathématicien Petre (Pierre) Sergescu, historien des sciences, personnalité du XXe siècle"
HerléaAlexandreAlexandre HERLEA est membre de la section « Sciences, histoire des sciences et des techniques et archéologie industrielle » du CTHS. Professeur émérite des universités, membre effectif de l'Académie
-
Webinaire sur la rédaction des PGD
LouvetViolaineRédaction des Plans de Gestion de Données (PGD) sous l’angle des besoins de la communauté mathématique.
-
Alexandre Booms : « Usage de matériel pédagogique adapté en géométrie : une transposition à interro…
« Usage de matériel pédagogique adapté en géométrie : une transposition à interroger ». Alexandre Booms, doctorant (Université de Reims Champagne-Ardenne - Cérep UR 4692)
-
Y. Lai - A family of 3d steady gradient Ricci solitons that are flying wings
LaiYiWe find a family of 3d steady gradient Ricci solitons that are flying wings. This verifies a conjecture by Hamilton. For a 3d flying wing, we show that the scalar curvature does not vanish at
-
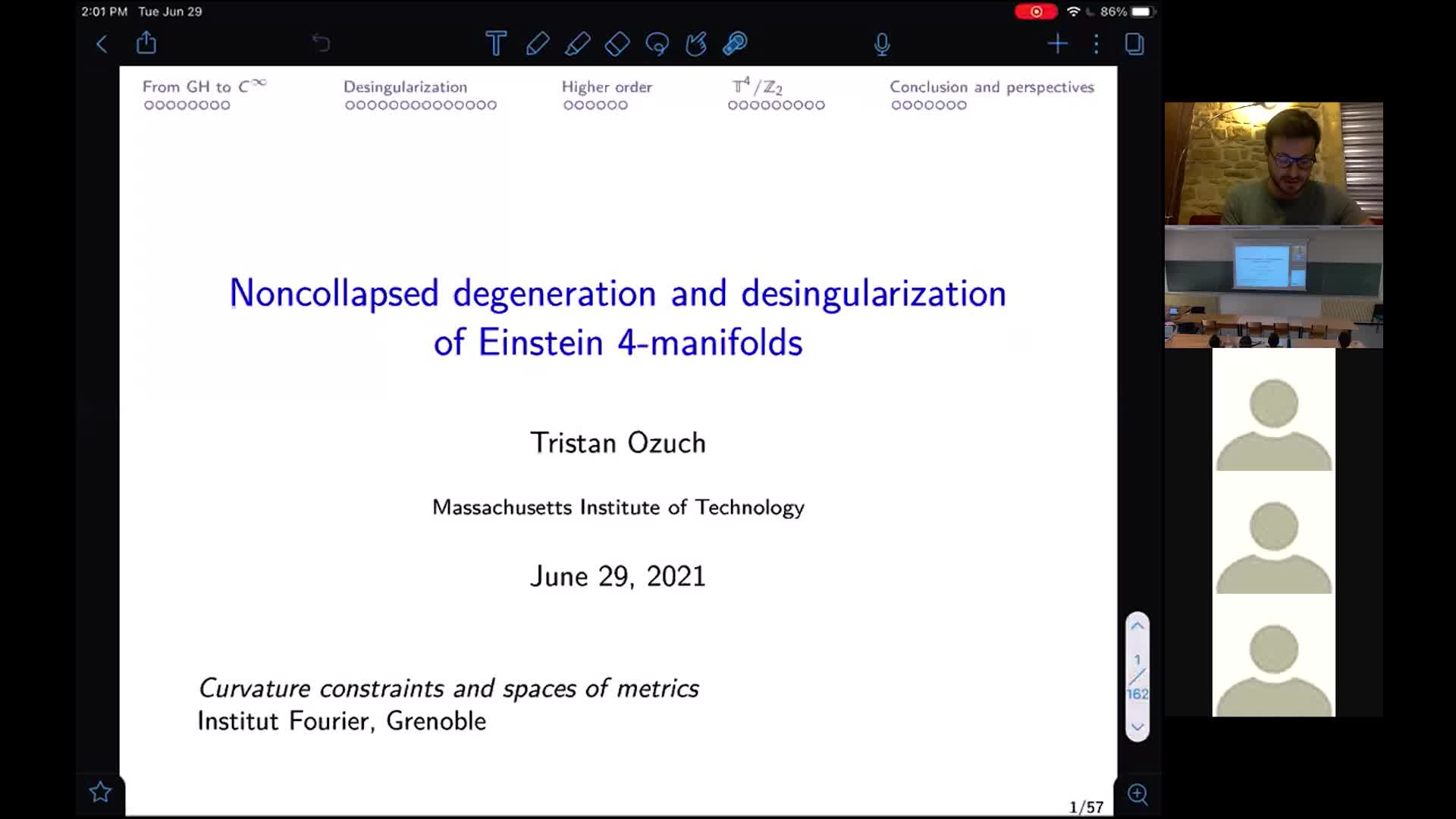
T. Ozuch - Noncollapsed degeneration and desingularization of Einstein 4-manifolds
OzuchTristanWe study the noncollapsed singularity formation of Einstein 4-manifolds. We prove that any smooth Einstein 4-manifold close to a singular one in a mere Gromov-Hausdorff (GH) sense is the result
-
D. Tewodrose - Limits of Riemannian manifolds satisfying a uniform Kato condition
TewodroseDavidPresentation of a joint work with G. Carron and I. Mondello where we study Kato limit spaces.
-
A. Mondino - Time-like Ricci curvature bounds via optimal transport
MondinoAndreaThe goal of the talk is to present a recent work in collaboration with Cavalletti (SISSA) on optimal transport in Lorentzian synthetic spaces. The aim is to set up a “Lorentzian analog” of the
-
M. Lesourd - Positive Scalar Curvature on Noncompact Manifolds and the Positive Mass Theorem
LesourdMartinThe study of positive scalar curvature on noncompact manifolds has seen significant progress in the last few years. A major role has been played by Gromov's results and conjectures, and in
-
J. Wang - Topological rigidity and positive scalar curvature
WangJianIn this talk, we shall describe some topological rigidity and its relationship with positive scalar curvature. Precisely, we will present a proof that a complete contractible 3-manifold with
-
R. Perales - Recent Intrinsic Flat Convergence Theorems
PeralesRaquelThéorèmes récents de convergence plane intrinsèque
-
J. Fine - Knots, minimal surfaces and J-holomorphic curves
FineJoëlI will describe work in progress, parts of which are joint with Marcelo Alves. Let L be a knot or link in the 3-sphere. I will explain how one can count minimal surfaces in hyperbolic 4-space
